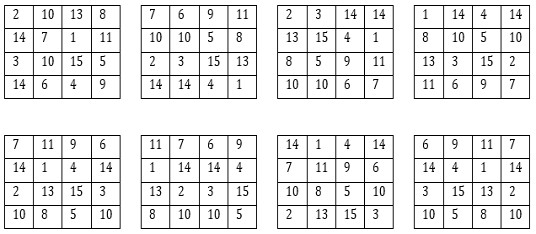
Sur l’une des façades de la « Sagrada Familia », la cathédrale de Barcelone, se trouve sculpté dans la pierre, un carré numérique, dont la constante « magique » est M’4 = 33, soit l’âge présumé de Jésus Christ lorsqu’il a été crucifié. Notons également que la somme des quatre cases centrales est également égale à 33.
C’est Antoni Gaudi ( 1852 – 1926 ), un architecte catalan, qui a conçu dans son ensemble la « Sagrada Familia », une œuvre encore inachevée. Les travaux ont débutés en 1882 ; à la mort d’Antoni Gaudi, c’est Domenec Sagranes, un collaborateur de Gaudi, qui poursuivit la construction de cette basilique, jusqu’en 1936 ; les travaux se sont alors poursuivis et sont toujours en cours, sous la direction de divers architectes successifs. On pense que l’édifice sera achevé, selon les plans de Gaudi, vers 2030.



En réalité, le carré magique qui nous intéresse, a été sculpté par Joseph Maria Subirachs en 1987, et serait de sa propre conception. Mais on l’appelle cependant « Le Carré de Gaudi ».
Ce carré numérique, dont la « magie » des lignes, des colonnes et des deux diagonales principales se retrouve dans plusieurs autres formations de quatre nombres, n’a rien de mystérieux.
Sommaire
Construction
Voici comment Subirachs a pu l’obtenir ; il avait deux possibilités, à partir de deux carrés magiques normaux d’ordre n = 4.
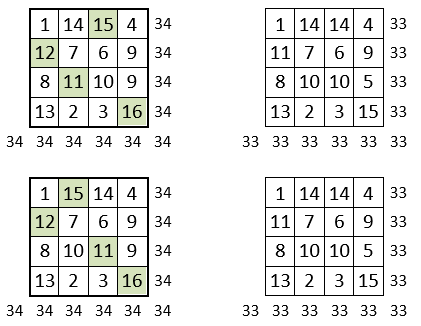
Pour obtenir la somme constante M’4 = 33, on enlève une unité, dans l’un ou l’autre des carrés magiques normaux ci-dessous, aux nombres situés sur une permutation figurée : on obtient le « Carré de Gaudi », dans lequel les nombres 12 et 16 sont absents, alors que les nombres 10 et 14 sont redoublés : ce n’est donc pas un carré magique normal ( A remarquer que le carré magique de gauche ci-dessous, est le carré magique dit de Dürer, après une rotation de 180° )

Il y a 24 permutations figurées dans une grille numérique normale d’ordre n = 4. On peut donc créer, à partir d’un carré magique normal d’ordre n = 4, 24 « Carrés de Gaudi » différents, de somme « magique » M’4 = 33. Et en utilisant les 880 carrés magiques de base de la classification de Frénicle, le nombre total N de carrés de type « Carrés de Gaudi » que l’on peut ainsi créer est : N = 24 x 880 = 21 120, ces grilles comprenant des redoublements et des disparitions de certains nombres.
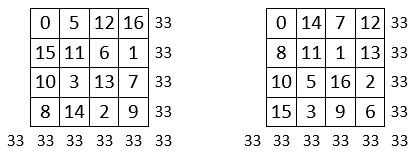
Voici deux Carrés magiques de Gaudi, de somme magique M’4 = 33, obtenus avec la série « 0, 1, 2, . . .16 », avec une seule disparition, celle du chiffre 4 : on ne peut sans doute pas faire mieux.
Propriété : La rotation invariante du « Carré de Gaudi »
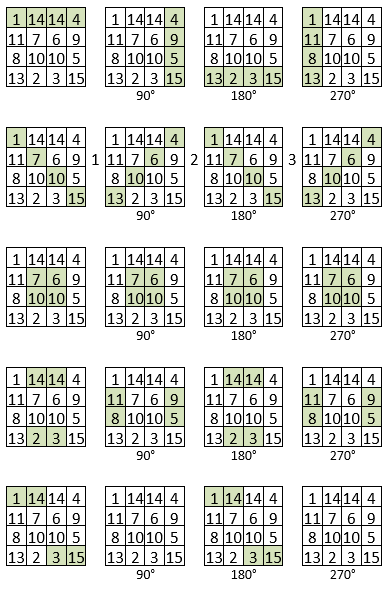
Le Carré de Gaudi présente un certain nombre d’invariants dans les trois rotations successives. Ces invariants correspondent aux formations « magiques » dudit carré de Gaudi.
Les grilles ci-dessous présentent à la fois les formations magiques et les invariants correspondants dans le carré de Gaudi, soit huit Rotations Invariantes Complètes ( RIC ), et deux Rotations Invariantes Simples ( RIS ) :

Propriété : Groupements de 4 termes dont la somme est égale à 33
Remarquons tout d’abord qu’une recherche analogue a été faite pour le carré magique normal d’ordre n = 4, en prenant pour exemple le carré magique dit de Dürer. Il s’agit des combinaisons des 16 premiers entiers pris 4 à 4, dont la somme est égale à la constante magique M4 = 34. Il y a alors 86 combinaisons possibles.
La question, avec le carré numérique de Gaudi, se présente un peu différemment.
En effet, du fait de la présence de deux doublets ( 14, 14 et 10, 10 ) dans la série de Gaudi, il faut envisager deux présentations différentes des solutions du problème en cause.
Chaque fois que le nombre 14, ou le nombre 10 apparaît dans la combinaison numérique de 4 termes, on peut écrire un doublet graphique, ou géométrique, soit deux solutions au total.
Lorsque 14 et 10 apparaissent en même temps, on peut écrire 3 doublets graphiques, soit quatre solutions au total.
Par contre, lorsque 14 et 14, ou bien 10 et 10, apparaissent dans une combinaison de 4 termes, il n’y a aucun doublet graphique
Ainsi on peut donc envisager :
. Une présentation ou visualisation graphique, tenant compte de tous les doublets
. Une présentation numérique ou arithmétique, ne tenant pas compte des doublets
Voici cette présentation numérique des 54 combinaisons numériques des 16 termes de la série
du carré numérique de Gaudi, pris 4 à 4, totalisant 33.
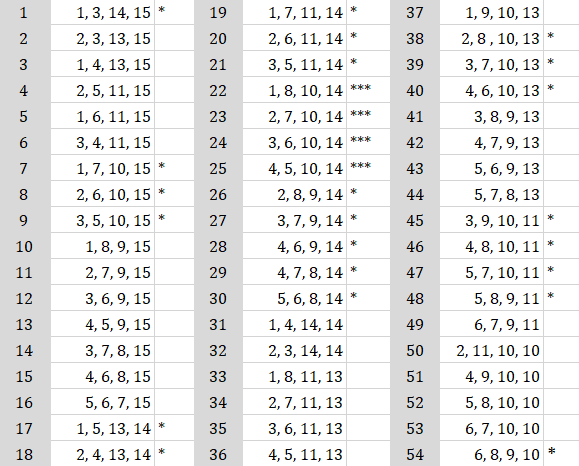
Les combinaisons pointées correspondent aux solutions « graphiques » ou « géométriques » comportant des doublets. Il y aurait ainsi 34 doublets graphiques ou géométriques, portant le nombre correspondant de solutions graphiques à :
54 + 34 = 88
On peut encore se poser la question suivante : « Avec la série numérique de 16 éléments de Gaudi, peut-on construire d’autres carrés numériques d’ordre n = 4, de constante linéaire 33 dans les lignes, les colonnes et les diagonales principales ? » Voici quelques solutions dues à Arsène Durupt. Il y en a d’autres : on pourra appeler à l’aide les 880 carrés magiques normaux de base d’ordre n = 4 ( Classification de Frénicle )