Sommaire
Quelques définitions
Les nombres complémentaires
Dans la suite naturelle des nombres entiers de 1 à N, on appelle » nombres complémentaires » les couples formés de deux nombres symétriques par rapport au milieu de la suite, paire ou impaire.
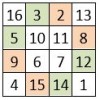
Par exemple, dans la suite des nombres de 1 à N = 16, ci-dessous :
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
les couples 1-16, 2-15, 3-14, 4-13 etc… sont formés de nombres complémentaires.
On observe que – la somme de deux nombres complémentaires est constante et égale à N + 1. – dans une suite impaire, le terme médian M est égale à ½ (N + 1).
Les cases complémentaires
Dans une grille carrée ou rectangulaire, on appelle « cases complémentaires », les cases diamétralement opposées, c’est-à-dire symétriques par rapport au centre de cette grille, paire ou impaire.
Les carrés magiques normaux de type associé
Cette disposition correspond au type de base III de la Classification de Dudeney. Voici quelques exemples.
Les 8 formes du Lo Shu correspondent à des carrés magiques du type « associé ».
Les carrés magiques associés, relativement peu nombreux dans la grande famille des carrés magiques normaux, sont cependant omniprésents dans tous les ouvrages traitant des carrés magiques , souvent de façon anonyme.
Propriétés générales des carrés magiques de type associé
❶ – Dans un carré magique associé, la somme P de deux nombres complémentaires est égale à P = ( n2 + 1 ) : cette constante numérique est appelée « constante de polarisation » par le général Cazalas.
❷ – Dans le cas d’une grille impaire, le terme médian M de la suite naturelle des entiers de 1 à N, avec N = n2, se trouve dans la case centrale de la grille, et vaut M = ½ ( n2 + 1 ), c’est-à-dire Mn/n. La réciproque n’est pas vraie.
❸ – Toujours dans le cas d’une grille impaire, le terme médian M dans la case centrale, est égal à la différence, en valeur absolue, entre les couples de nombres comptés à partir d’une case angulaire, en tournant toujours dans le sens approprié, pour aboutir à la case centrale.
Ainsi dans l’exemple ci-dessus, pour n = 5 : 15 – 2 = 13 ; 19 – 6 = 13 ; 23 – 10 = 13 ; etc…
❹ – Les carrés magiques de type associé, sont semipandiagonaux, c’est-à-dire que la constante magique est obtenue dans les seules diagonales brisées dont les termes présentent une symétrie centrale. Exemple dans le carré magique de type associé, dit de Dürer : Dans les diagonales brisées en cause, on a ainsi :
5 + 3 + 14 + 12 = 34 et 9 + 15 + 8 + 2 = 34
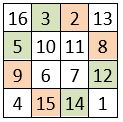
❺ – Les carrés magiques de type associé sont autocomplémentaires.
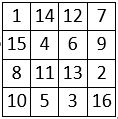
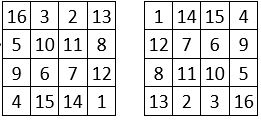
Lorsque l’on remplace chaque terme d’un carré magique normal d’ordre n, par son complément à [n2 + 1], on obtient un autre carré magique de même constante linéaire, dit « complémentaire » et l’opération est réversible. Exemple : avec n = 4 ; n2 + 1 = 17
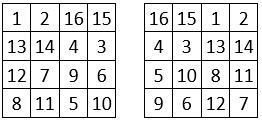
Dans le cas du carré magique de type associé, le « complémentaire » coïncide, après une rotation, avec le carré magique d’origine : ce dernier est alors dit « autocomplémentaire ». Exemple ci-contre :
❻ – Il n’existe pas de carré magique de type associé d’ordre impairement pair, c’est-à-dire divisible une seule fois par 2 , comme n = 6, 10, 14, 18, 22, . . .
Les carrés magiques de type associé n =4
Lorsque l’on accole deux couples quelconques de nombres complémentaires, la somme des 4 nombres ainsi groupés, est constante. Cela résulte directement de la propriété I énoncée ci-dessus, et cette somme vaut donc 2 (n2 + 1) = 2 P, soit le double de la constante de polarisation.
Cette remarque est particulièrement intéressante dans le cas des carrés magiques associés d’ordre n = 4, car cette somme, soit 2 ( n2 + 1 ) = 34, est précisément égale à la constante magique des carrés magiques normaux d’ordre n = 4.
Soit un carré magique associé d’ordre n = 4 : le carré dit de Dürer, par exemple :
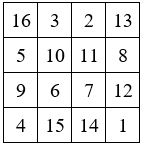
Il y a 8 couples de nombres complémentaires dans la suite des entiers de 1 à 16, que l’on peut identifier par les lettres A, B, C, D….H :
| 1 – 16 | 2 – 15 | 3 -14 | 4 – 13 | 5 – 12 | 6 – 11 | 7 – 10 | 8 – 9 |
| A | B | C | D | E | F | G | H |
Le groupement de deux couples de cette série de 8, s’identifie aux combinaisons de 8 termes 2 à 2.
Le nombre de combinaisons est alors ![]()
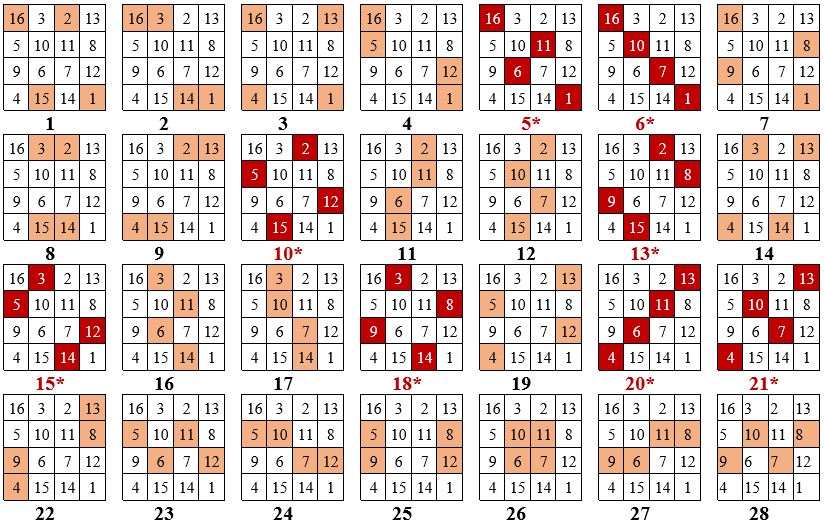
Il est facile de dresser le tableau de ces 28 combinaisons :
AB AC AD AE AF AG AH
BC BD BE BF BG BH
CD CE CF CG CH
DE DF DG DH
EF EG EH
FG FH
GH
La somme des 2 couples, soit 4 nombres, correspondant à ces 28 combinaisons, donne donc la constante magique M4= 34 du carré magique normal d’ordre n = 4
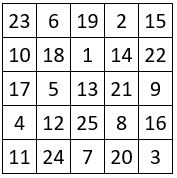
Les carrés magiques de type associé n =5
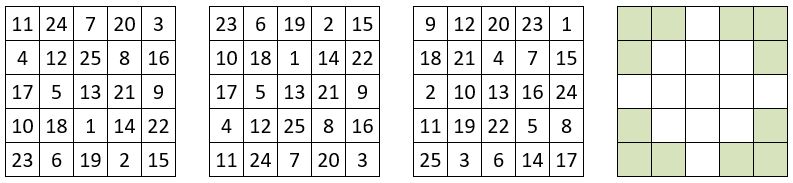
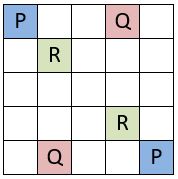
❶ Le total de deux nombres diamétralement opposés est constant, et égal à [n2 + 1] = 26 ( Rappel )
❷ Dans les quatre équerres aux sommets de la grille ( schéma ci-dessus ) les trois nombres ont 39 pour somme commune .
❸ On peut isoler neuf petites grilles cruciformes dont les axes sont formés de 3 cases ; les 3 termes sur ces axes donnent le même total, ce total étant propre et différent dans chaque grille cruciforme.
❹ La somme propre de deux grilles cruciformes symétriques par rapport au centre du carré magique, est constante et égale à 78.
❺ On peut tracer cinq pentagrammes irréguliers, dont la somme des nombres des cinq sommets situés sur l’enceinte périphérique donne toujours 65.
❻ On peut tracer deux hexagones irréguliers, dont les nombres aux 6 sommets situés sur l’enceinte périphérique ont 78 comme somme commune.
❼ Dans le carré central d’ordre n = 3, les médianes et les diagonales donnent une somme constante de 39.
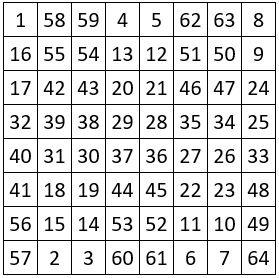
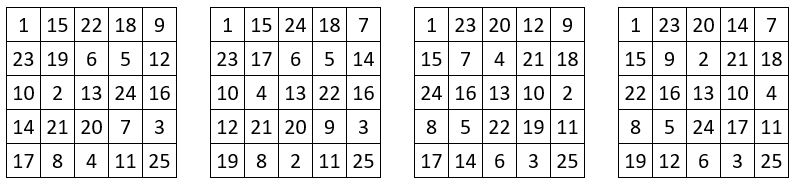
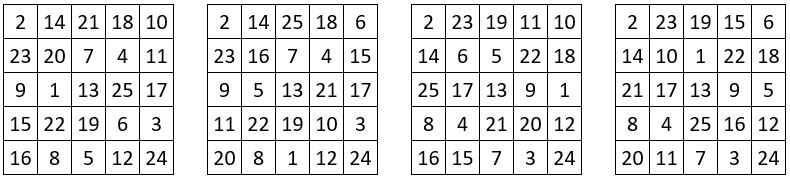
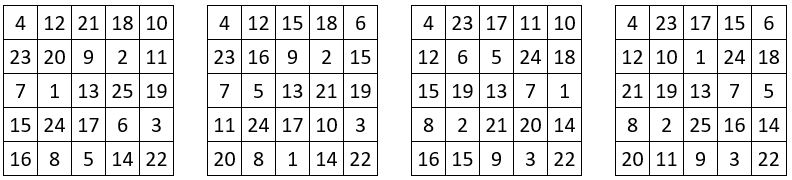
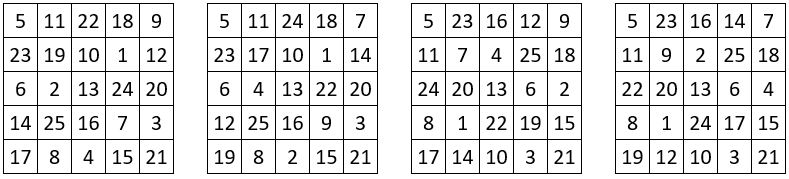
Les 16 carrés « supermagiques » japonais de type associé, d’ordre n = 5
Les 16 carrés magiques de type associé, que l’on trouve ci-dessous, présentent, en plus des propriétés mentionnées précédemment, les propriétés suivantes, qui leur confèrent une « supermagie » certaine :
❶ Dans toute fenêtre d’ordre n = 3, la somme des 4 sommets et du centre, est magique, soit 65.
❷ La somme des 4 sommets de la grille d’ordre n = 5, et du centre, est magique ( 65 )
❸ Dans toute formation cruciforme de 5 nombres, leur somme est magique ( 65 )
❹ Ces carrés « supermagiques » d’ordre n = 5 sont auto-complémentaires.
❺ Ces propriétés sont conservées dans le « tapis » correspondant, à l’exception de la propriété n°4 qui précède.
▶ Henry E. Dudeney (1917-1958) – Amusements in Mathematics – Dover Publications, New York
▶ Général Cazalas (1934) – Carrés magiques au degré n – Hermann Editeur, Paris
▶ William H. Benson & Ostwald Jacoby (1976) – New Recreations with Magic Squares – Dover Publications, New York.
▶ René Descombes (2000)– Les Carrés Magiques – Vuibert Editeur, Paris, 500 pp.
▶ Bernard Gervais (1998) – Les Carrés Magiques de 5 (Les mosaïques magiques) – Eyrolles Editeur, 195 pp.
▶ Mutsumi Suzuki – Ultra Magic Squares of 5 x 5 – Japan’s Tohoku University