

Dans le roman de Thomas Mann, « Le Docteur Faustus – La vie du compositeur allemand Adrian Leverkühn racontée par un ami » ( 1947 ), le narrateur, Serenus Zeitblom, s’exprime ainsi qu’il suit à propos de la chambre qu’occupe Adrian Leverkühn dans le ville de Halle .
Au-dessus, sur le mur, des punaises fixaient une gravure, un diagramme arithmétique déniché dans un bric-à-brac : un carré magique, comme on disait, tel qu’il figure à coté du sablier, du cercle de la balance et du polyèdre sur l’eau-forte de la Mélancholie de Dürer. Ici aussi, la figure se divisait en quatorze cases numérotées de chiffres arabes, de façon que le 1 se trouvait dans la case de droite du bas, le 16 dans celle de gauche en haut. Le prodige – ou la curiosité – consistait en ce que ces nombres, de quelque manière qu’on les additionnât, de haut en bas, en travers ou en diagonale, donnaient toujours le total de 34. De quel principe d’ordonnance procédait cette constante magie ? Je n’ai jamais pu m’en rendre compte, mais peut-être à cause de la place en vue, au dessus-de l’instrument, qu’Adrian avait attribuée à cette gravure, elle attirait sans cesse le regard. je crois qu’à aucune de mes visites je ne manquais de vérifier d’un rapide coup d’œil oblique, de haut en bas ou de bas en haut, la concordance fatidique.
Nous nous proposons de décrypter ce carré magique, punaisé dans la chambre d’Adrian Leverkühn à Halle, et évoqué sommairement par le narrateur.
Il s’agit d’un carré magique d’ordre n = 4, dans une grille de 16 cases ( et non pas quatorze comme le dit le narrateur – 1) dont on ne connait que deux nombres, placés aux extrémités de la première diagonale. On connait aussi la constante magique, 34.
Bien sûr on peut penser qu’il s’agit du carré magique placé par Albrecht Dürer dans sa gravure « Melencolia » ( 1514 ). C’est vraisemblable, mais ce n’est qu’une supposition du narrateur.
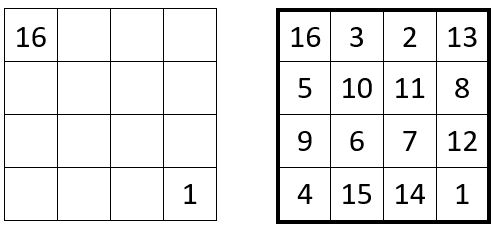
On peut alors se demander s’il existe d’autres carrés magiques normaux d’ordre n = 4, comportant les deux nombres « 16 » et « 1 » placés aux extrémités de la première diagonale ?
Cette recherche a été tentée : le problème a en effet été soulevé par Marc Laura dans le supplément n° 77 de la Revue « Tangente ». Cependant Marc Laura expose une méthode qui ne donne qu’un certain nombre de solutions.
On peut conjecturer que le « carré magique de Thomas Mann » est de type associé, cette remarque est essentielle. Rappelons que dans un carré magique de type associé, les nombres complémentaires placés dans les cases complémentaires, ont pour somme constante P = n2 + 1, soit dans notre cas, P = 16 + 1 = 17. Et l’on sait qu’il existe 48 carrés magiques de type associé parmi les 880 carrés magiques de base d’ordre n = 4 de la Classification du mathématicien français Bernard Frénicle de Bessy ( 1605 – 1675 ) .
Le ou les carrés magiques de Thomas Mann doivent nécessairement se retrouver parmi ces 48 carrés magiques de base de type associé, car il n’y en a pas d’autres !
Une méthode triviale, sans avoir recours à des calculs, permet alors de résoudre simplement et complètement le problème. On peut rapidement sélectionner ces 48 carrés magiques associés dans la liste donnée par Benson & Jacoby : ils sont du type III de la classification de Dudeney, et le type correspondant est donné pour chaque carré magique de cette liste (Numérotation de Frénicle).
Voici les 48 carrés magiques de type associé d’ordre n = 4, tels qu’ils se présentent dans l’ouvrage posthume de Bernard Frénicle de Bessy : Des quarrez magiques, paru en 1693 sous les auspices de Philippe de la Hire .

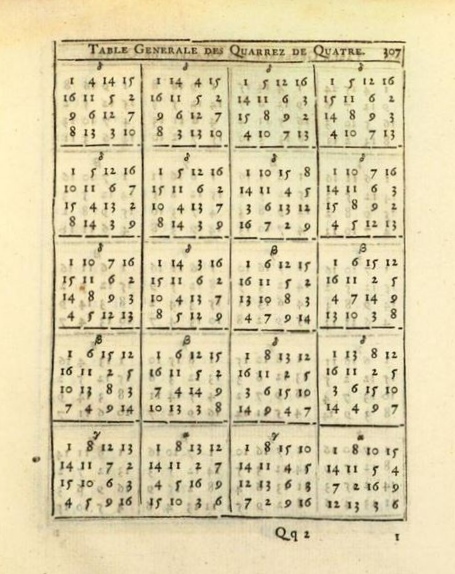

Parmi ces 48 carrés magiques de type associé d’ordre n = 4, on remarque 12 carrés magiques de la forme décrite par Thomas Mann, à une symétrie près : ce sont d’ailleurs les 12 premiers carrés de la collection des 48 carrés magiques de type associé de Frénicle.
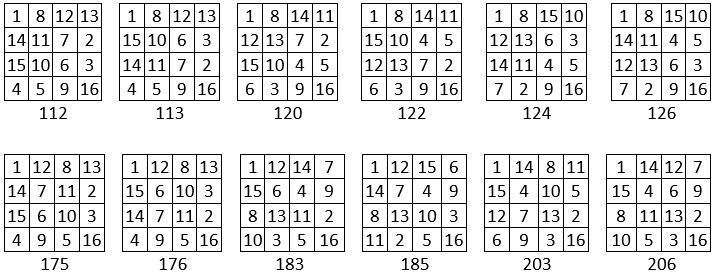
On constate cependant que certains couples de ces carrés, se déduisent l’un de l’autre à la suite de certaines manipulations, par exemple par la permutation des deux lignes ou des deux colonnes centrales. Ce sont les couples suivants :
112 et 113 ; 120 et 122 ; 124 et 126
175 et 176 ; 183 et 206 ; 185 et 203
De sorte que l’on ne peut retenir que six carrés magiques de type associé ayant les caractéristiques décrites par Thomas Mann :
112 ; 120 ; 124 ; 175 ; 183 et 185
Alors voici donc ces six carrés magiques de type associé, présentés sous la forme de Thomas Mann, soit les symétriques des carrés magiques correspondants qui précèdent, par rapport à la seconde diagonale :

Ces six carrés magiques de type associé de Thomas Mann peuvent alors donner au total 8 images différentes, par permutation des deux lignes médianes, permutation des deux colonnes médianes, cumul de ces deux manips, et enfin symétrie par rapport à la première diagonale principale qui seule conserve la disposition du couple « 16 – 1 » aux extrémités de cette première diagonale principale.
On a donc ainsi 6 x 8 = 48 solutions pour ces carrés magiques de Thomas Mann.
Voici ces 48 solutions de Thomas Mann, ce sont toutes les solutions possibles, il n’y en a pas d’autres ; le problème est complètement résolu.

A vrai dire, en réfléchissant, le carré magique n’est pas la seule figure présentant ces propriétés :
on peut présenter cette « grille magique » sous la forme d’un carré latin diagonal. On construit en effet facilement un carré latin diagonal comportant les nombres 1 et 16 aux extrémités de la première diagonale, et dont la somme des termes des lignes, des colonnes et des diagonales soit constante et égale à 34 : ce qui correspond bien aux vérifications de Serenus Zeitblom. On trouve même 14 solutions différentes à ce problème, en deux séries de sept :

