
Ératosthène de Cyrène est un astronome, géographe, philosophe et mathématicien grec du IIIe siècle av. J.-C.. Érudit reconnu par ses pairs, considéré comme le plus grand savant de son époque, il travailla dans les domaines des mathématiques, de l’astronomie, de la poésie, de l’histoire , de la musique….
Dans le domaine de la géographie, il a établi la première méthode de mesure de la circonférence de la Terre !
Dans le domaine des mathématiques, il mit au point une méthode (le crible) qui permet de déterminer tous les nombres premiers.
On a l’habitude de présenter le Crible d’Eratosthène pour les cent premiers nombres, dans un carré naturel d’ordre n = 10, de 100 cases ( 1 )
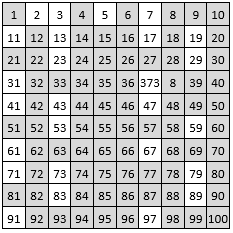
On occulte ou poche successivement les nombres de ce carré naturel qui ne sont pas premiers.
On poche 1 qui est considéré comme n’étant pas premier.
2, 3, 5, 7 et 11 sont les nombres premiers successifs : on poche les multiples de 2, de 3, de 5, de 7 et de 11. Tous les nombres non pochés de la grille sont des nombres premiers, avec une répartition au hasard dans cette grille, sans aucune règle apparente.
Cependant la présentation du Crible d’Eratoshène dans une grille rectangulaire à 6 colonnes, 6 x 17, de 102 cases, offre des caractéristiques particulièrement intéressantes. On procède alors comme précédemment, pour le carré naturel de 100 cases.
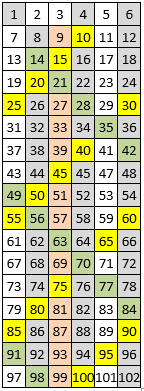
Dans la grille ci-contre, le premier nombre premier est 2.
On élimine en les pochant ( en gris ) tous les nombres multiples de 2, soit les nombres pairs des colonnes 2, 4 et 6.
Le nombre premier suivant est 3 : on poche tous les multiples de 3 dans la colonne 3 ( en sépia )
Le chiffre 5 est le nombre premier qui suit. On poche ( en jaune ) les multiples de 5 dans quatre diagonales, dont certains sont déjà pochés.
On poche ensuite les multiples de 7 ( en vert ), dont certains sont également déjà pochés. On s’arrête là, les multiples de 11 étant déjà pochés.
On constate alors que les nombres premiers situés dans les cases non pochées, se trouvent tous concentrés ( à l’exception de 2 et 3 ) dans les colonnes 1 et 5 de manière consécutive en descendant dans la grille.
Et l’on observe que tous ces nombres premiers précèdent ou suivent immédiatement un multiple de 6.
Cette observation mérite que l’on s’y attarde. On peut formuler la propriété ci-dessus comme suit :
Tout nombre premier est de la forme 6 k – 1 ou 6 k + 1.
Mais la réciproque n’est pas vraie : tout nombre de la forme 6 k – 1 ou 6 k + 1 n’est pas un nombre premier. Il y a de nombreux exemples, ainsi :
91 – 1 = 90 est divisible par 6, mais 91 n’est pas premier ( multiple de 7 );
305 + 1 = 306 est divisible par 6, mais 305 n’est pas premier ( multiple de 5 ) ;
341 + 1 = 342 est divisible par 6, mais 341 n’est pas premier ( multiple de 11 ) . . .
On voit d’ailleurs très bien, dans la grille à six colonnes ci-dessus, que tous les nombres des colonnes « 1 » ( de la forme 6 k + 1 ) et « 5 » ( de la forme 6 k – 1 ), ne sont pas des nombres premiers.
Si l’on prolonge cette grille rectangulaire à l’infini vers le bas, en procédant aux éliminations « pochées » comme cela a été fait précédemment pour les 100 premiers nombres dans le carré naturel et dans la grille rectangulaire 6 x 17, il apparait que tous les nombres premiers restent bien dans les colonnes 1 et 5 de manière consécutive, et toujours avec la même propriété énoncée ci-dessus.
Cette grille rectangulaire se présente ainsi comme une vraie table des nombres premiers, assortie d’une répartition bien définie de ces nombres premiers dans deux colonnes.
Cette présentation semble inédite. Mise à part la spirale d’Ulam, qui est partielle, on n’avait pas trouvé une représentation complète des nombres premiers consécutifs dans l’espace.
Corolaire : les Nombres premiers jumeaux.
La colonne « 6 » de la grille rectangulaire ci-dessus, éventuellement complétée vers le bas, donne tous les multiples consécutifs de 6, sans omission ( 2 )
Il s’ensuit que tout nombre multiple de 6, auquel on ajoute ou retranche l’unité, donne un nombre premier dans l’une ou l’autre de ces deux opérations, et parfois deux nombres premiers : ainsi par exemple 72 donne 71 et 73 ; 810 donne 809 et 811 . . .
Dans ce dernier cas, on nomme ces couples de nombres premiers qui présentent un écart de 2 unités, « Nombres premiers jumeaux ».
On peut ainsi définir que tout couple de nombres premiers jumeaux est de la forme :
« 6 k – 1, 6 k + 1 »
Comme pour les nombres premiers, il y a une infinité de nombres premiers jumeaux, bien que cela ne soit pas démontré.
Voici les cinquante premiers Nombres premiers jumeaux, présentant un écart de 2 unités, qui figurent dans la grille à six colonnes « prolongée, laquelle peut être considérée aussi comme une vraie table des nombres premiers jumeaux ( 3 ) :
| 3, 5 | 5, 7 | 11, 13 | 17, 19 | 29, 31 |
| 41, 43 | 59, 61 | 71, 73 | 101, 103 | 107, 109 |
| 137, 139 | 149, 151 | 179, 181 | 191, 193 | 197, 199 |
| 227, 229 | 139, 241 | 269, 271 | 281, 283 | 311, 313 |
| 347, 349 | 419, 421 | 431, 433 | 461, 463 | 521, 523 |
| 569, 571 | 599, 601 | 617, 619 | 641, 643 | 659, 661 |
| 809, 811 | 821, 823 | 827, 829 | 857, 859 | 881, 883 |
| 1019, 1021 | 1031, 1033 | 1049, 1051 | 1061, 1063 | 1091, 1093 |
| 1151, 1153 | 1229, 1231 | 1277, 1279 | 1289, 1291 | 1301, 1303 |
| 1319, 1321 | 1427, 1429 | 1451, 1453 | 1481, 1483 | 1487, 1489 |
1 ) René Descombes – Le Carré naturel, problèmes et jeux – Editions Nuvis 2011 – pp. 81-82.
2 ) Alex Bellos – Alex et la Magie des Nombres – Editions Robert Laffont 2015 – pp. 282 – 283.
3 ) Jean-Paul Delahaye – Merveilleux nombres premiers – Voyage au cœur de l’arithmétique – Belin – Pour la Science, 2000, p. 233.
