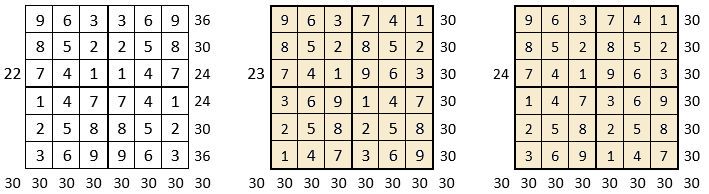
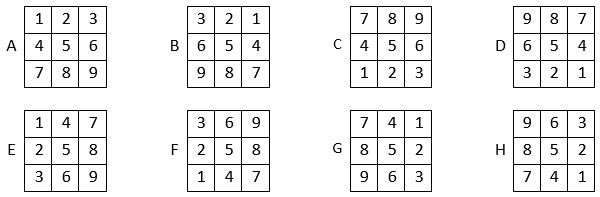
Le carré naturel d’ordre n = 3 se présente sous les huit formes classiques ci-dessous.
On propose d’assembler au carré, quatre de ces grilles, de façon à obtenir une grille « magique » d’ordre n = 6 de 36 cases. On demande de dénombrer ces assemblages magiques, et d’en dresser le catalogue.
On dénombre : ![]() combinaisons de ces 8 formes du carré naturel d’ordre n = 3, prises 4 par 4.
combinaisons de ces 8 formes du carré naturel d’ordre n = 3, prises 4 par 4.
Voici le tableau de ces 70 combinaisons : Tableau I.
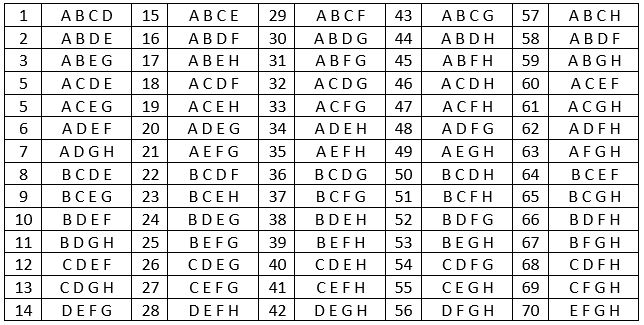
Mais ce n’est pas tout. Les 4 termes de chaque combinaison peuvent se présenter dans un ordre différent, correspondant aux permutations de ces 4 termes, soit : P4 = 4 ! = 24.
Au total on a donc : N = 70 x 24 = 1 680 solutions théoriques, dont il s’agit de tester la « magie ».
Combinaison A, B, C, D ( N° 1 )
Prenons pour exemple la première combinaison du tableau ci-dessus, le N° 1 : A, B, C, D.
Voici comment on peut procéder
Les 24 permutations des termes A, B, C, D se présentent ainsi, dans le Tableau II ci-dessous :
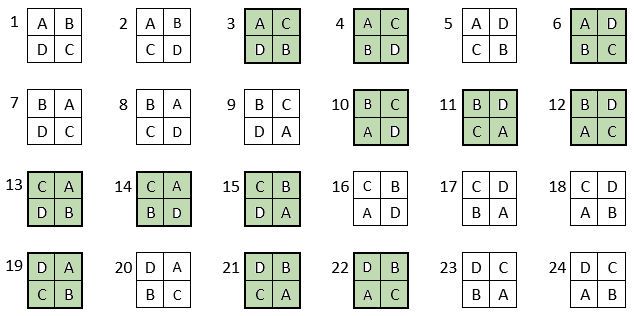
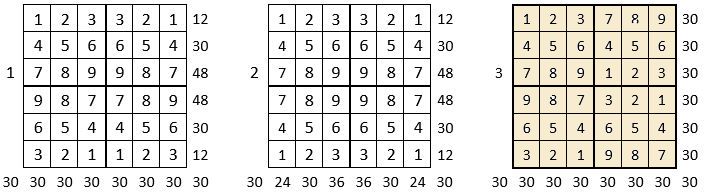
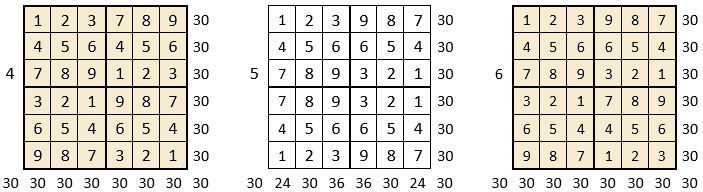
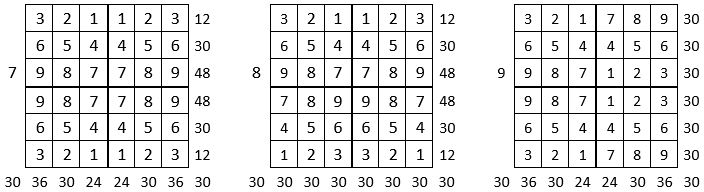
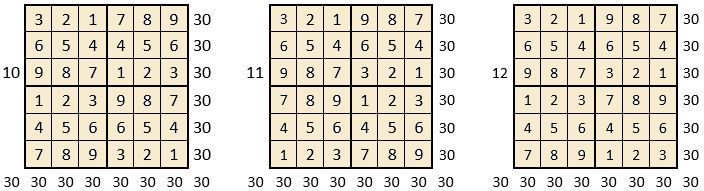
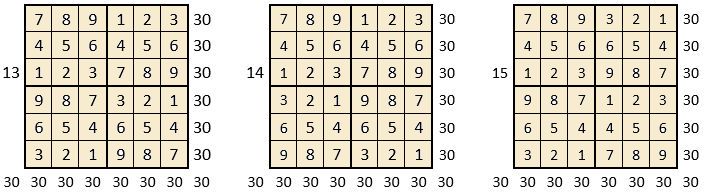
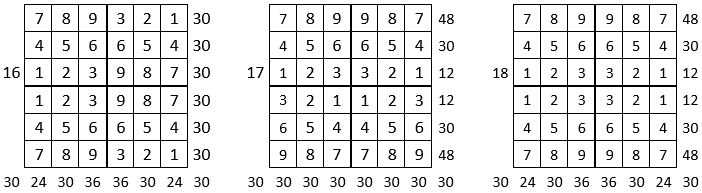
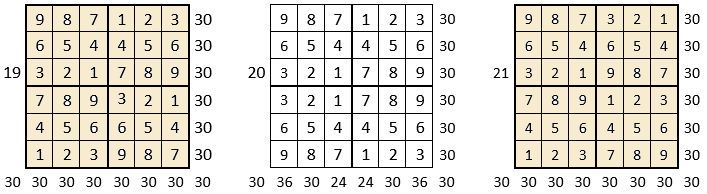
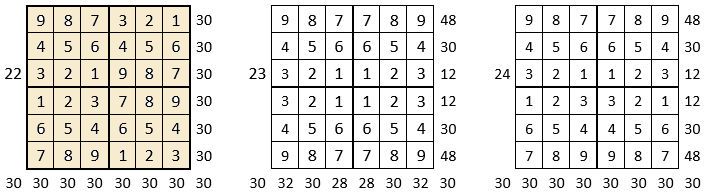
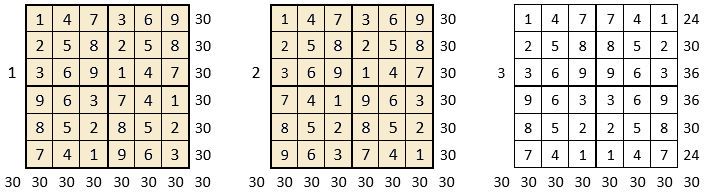
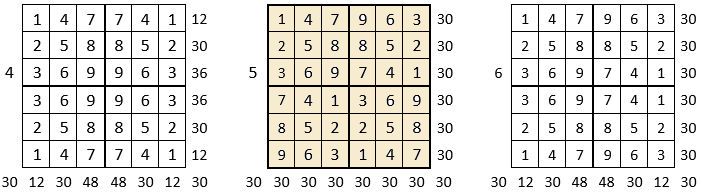
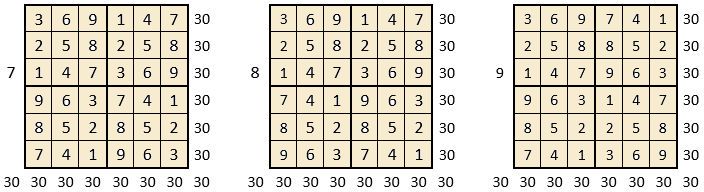
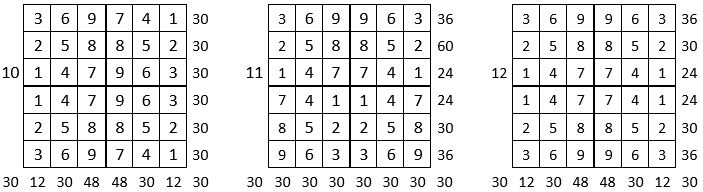
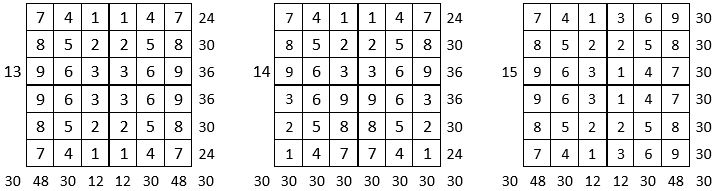
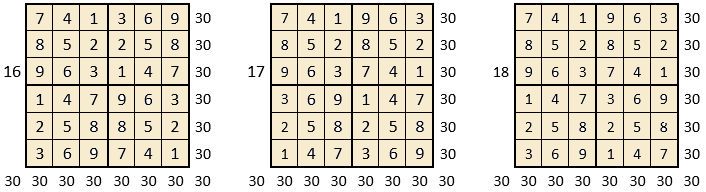
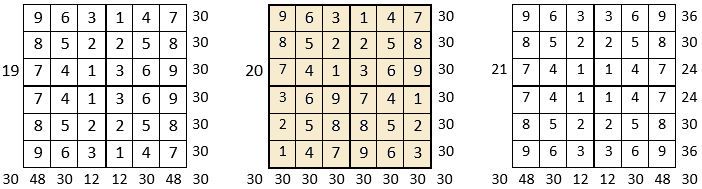
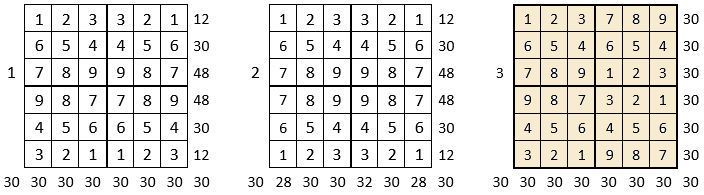
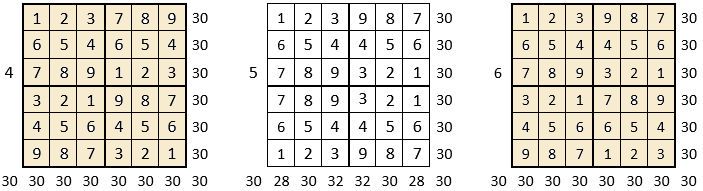
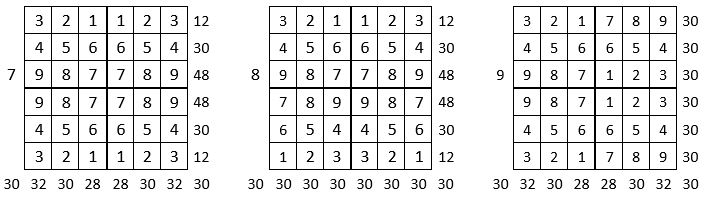
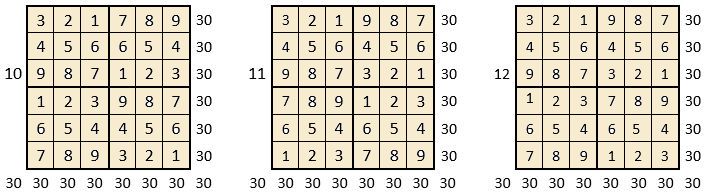
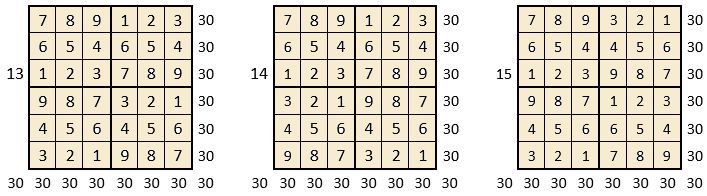
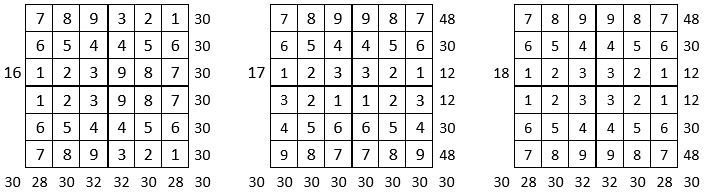
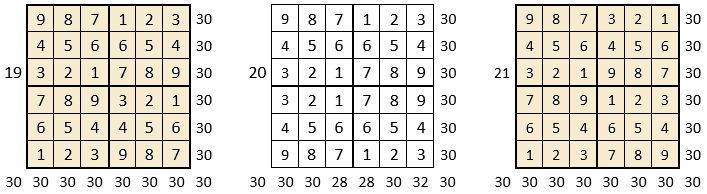
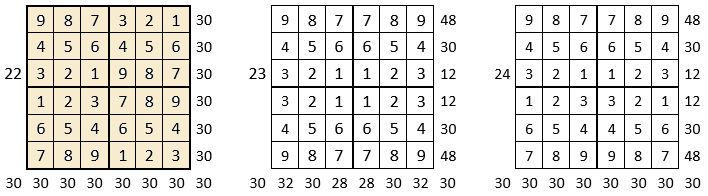
On peut alors dresser l’ensemble des 24 assemblages de la combinaison des quatre formes A, B, C, D du carré naturel d’ordre n = 3, dont il s’agira ensuite de tester la « magie », l’un après l’autre :
Après avoir testé la « magie » de chacun des 24 assemblages ci-dessus, on compte douze assemblages « magiques » dans les lignes, les colonnes et les deux diagonales principales ( encadrés ci-dessus, et encadrés aussi dans le Tableau II précédent) : ce sont les 12 numéros suivants ;
3, 4, 6, 10, 11, 12, 13, 14, 15, 19, 21 et 22,
c’est-à-dire la moitié du nombre total de 24 assemblages possibles dans cette combinaison.
Remarque : les assemblages magiques de base d’ordre n = 3 ( d’après Michel Criton )
A l’issue du développement ci-dessus, on remarque que les « assemblages magiques » pris parmi les huit formes du carré naturel d’ordre n = 3, sont en nombre relativement restreint, et sont les suivants :
Horizontalement : A C ou C A A D ou D A B D ou D B B C ou C B
E F ou F ER E H ou H E F G ou G H G H ou H G
Verticalement : A D ou D A A B ou B A B C ou C B C D ou D C
E H ou H E E G ou G E F G ou G F F H ou H FH F
On a ainsi seulement six assemblages magiques de base, les autres assemblages se déduisant par des rotations et/ou des symétries de ces derniers :

On retrouve bien cette propriété dans les douze assemblages « magiques » des combinaisons détaillées ci-dessus.
Dans la combinaison « A, B, C, D » ( le numéro entre crochets indique l’assemblage de base ) :
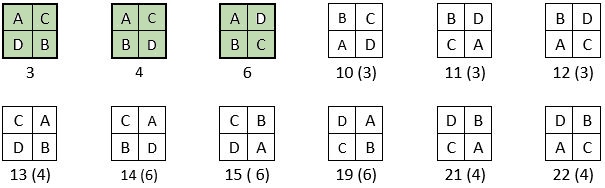
On obtiendrait donc seulement 24 assemblages magiques types sur les 1 680 assemblages possibles.
Combinaison E, F, G, H ( N° 70 )
On peut alors appliquer le mode opératoire ci-dessus à la dernière combinaison sélectionnée d’après la remarque ci-dessus, c’est-à-dire la combinaison : E, F, G, H ( N° 70 ); les 24 permutations se présentent ainsi, dans le Tableau III ci-dessous :
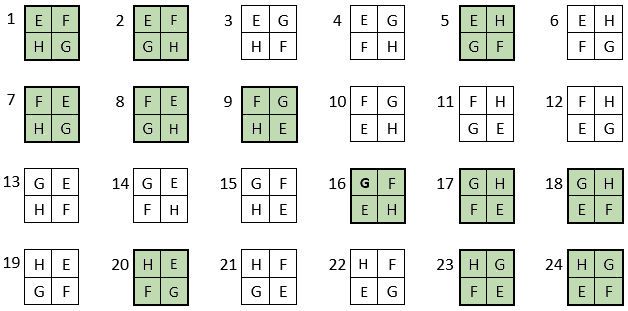
On peut alors dresser l’ensemble des 24 assemblages de la combinaison des quatre formes E, F, G, H du carré naturel d’ordre n = 3, dont il s’agira ensuite de tester la « magie », l’un après l’autre :
Pour cette combinaison E, F, G, H, on constate bien qu’il y a également 12 assemblages « magiques » ; ces assemblages « magiques » correspondent, dans les Tableaux II et III superposés, aux numéros des assemblages non magiques de la combinaison A, B, C, D : Et les deux combinaisons sont elles-mêmes diamétralement symétriques, ou symétriques par rapport au centre du Tableau I des 70 combinaisons :

On retrouve bien, dans la combinaison E, F, G, H, cette propriété dans les douze assemblages « magiques » des combinaisons détaillées auparavant :
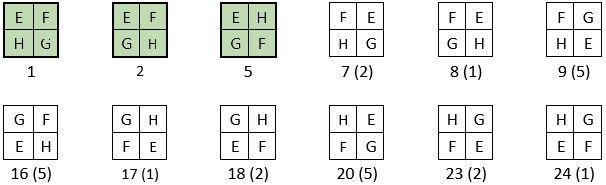
On peut alors regrouper en un seul Tableau IV les 24 assemblages magiques des 8 formes du carré naturel d’ordre n = 3, , avec leurs numéros correspondants dans les combinaisons A, B, C, D ( N° 1 ) pour les 12 premiers, et E, F, G, H ( N° 70 ) pour les 12 derniers : Tableau IV.
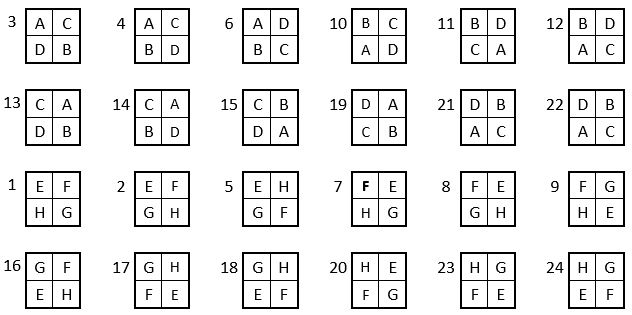
Ce Tableau IV condense le dénombrement et le catalogue des assemblages « magiques » des huit formes du carré naturel d’ordre n = 3 prises 4 à 4, et répond aux questions posées dans les données du problème.
La constante linéaire S3 = 30, est égale au double de la constante magique : M3 = 15, du carré magique normal de même ordre, n = 3, le Lo Shu.
Rappelons que cette constante linéaire de 30, est l’hypoténuse du triangle rectangle dont les autres côtés sont 18 et 24 : 182 + 242 = 302. Et 30 c’est aussi le Département du Gard, ce qui n’a rien à voir.
Propriétés des assemblages magiques
Les propriétés des assemblages magiques d’ordre n = 6 de 36 cases, formés de 4 formes différentes du carré naturel d’ordre n = 3, sont liées aux propriétés de ce carré naturel de base d’ordre n = 3.
Ainsi dans chacun des quartiers de 9 cases des assemblages, qu’ils soient magiques ou non, les médianes et les diagonales totalisent chacune : M3 = 15, de sorte que les diagonales de tous les assemblages ont pour somme :
S = 2 M3 = 30.
Les quartiers sont de type associé, de constante de polarisation : P = n2 + 1 = 10.
La somme des termes des quartiers est constante et égale à : S = 45
Les deux lignes ou colonnes médianes des assemblages sont de somme constante : S = 30.
Les sommes linéaires sur les côtés de la grille, sont symétriques par rapport aux médianes.
Les assemblages du carré naturel alterné d’ordre n = 3
Nous allons suivre le même mode opératoire que ci-dessus, pour le carré naturel d’ordre n = 3.
Les 8 formes classiques du carré naturel alterné d’ordre n = 3, se présentent ainsi :
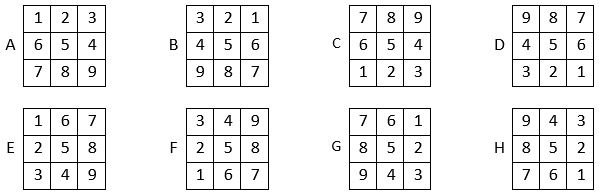
Voici les 24 assemblages correspondant à la première combinaison A, B, C, D ( N° 1 ) :
On constate que les douze grilles « magiques » issues du carré naturel alterné, dans la combinaison A, B, C, D, portent les mêmes numéros, c’est-à-dire correspondent aux mêmes assemblages, que dans l’application qui précède, formée de carrés naturels de même ordre.
On peut sans doute, pour le carré naturel alterné, adopter, mutatis mutandis, les mêmes conclusions que pour le carré naturel.
Application au carré naturel d’ordre n = 4
Peut-on envisager d’appliquer le même mode opératoire au carré naturel d’ordre n =4 ?
Le carré naturel d’ordre n = 4 se présente également sous les huit formes classiques ci-dessous :
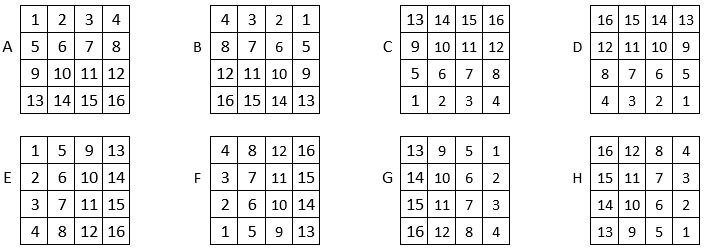
Il y a également 70 combinaisons de ces huit formes prises 4 à 4 ; et il y a aussi le même nombre, soit P4 = 24, de présentations des termes des grilles en cause.
On est donc amené à tester, comme précédemment, le même nombre d’assemblages pour chacune des 24 combinaisons. Prenons la première combinaison : A, B, C, D.
Peut-on se fier au Tableau II des assemblages, qui précède, établi pour les combinaisons A, B, C, D, du carré naturel n = 3 ?
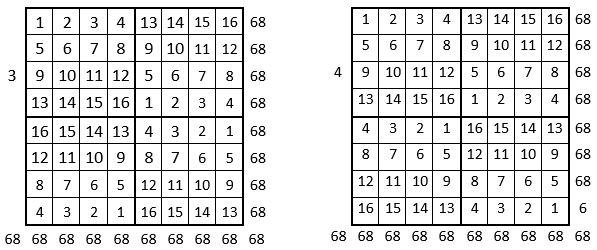
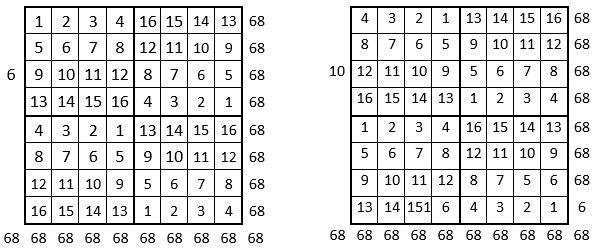
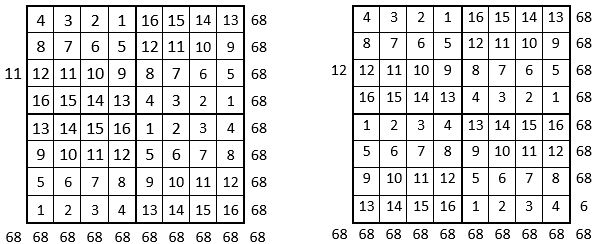
Les différentes applications concordent : on peut donc utiliser ce Tableau II, et ainsi dresser l’ensemble des douze grilles « magiques » correspondant aux assemblages des formes A, B, C, D du carré naturel d’ordre n = 4, dans cette première combinaison A, B, C, D.
La constante linéaire : S4 = 68, est égale au double de la constante magique : M4 = 34, du carré magique normal de même ordre, n = 4.
C’est aussi l’hypoténuse du triangle rectangle de côtés 32, 60, 68 : 682 = 322 + 602.
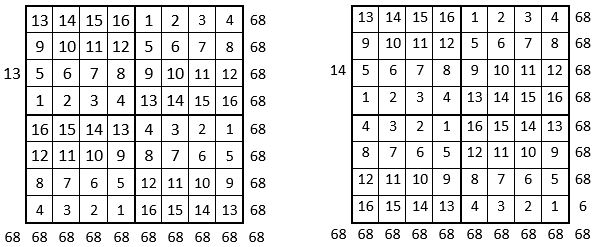
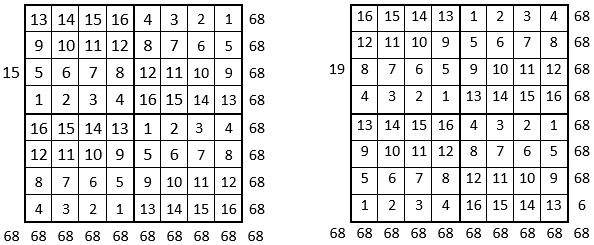
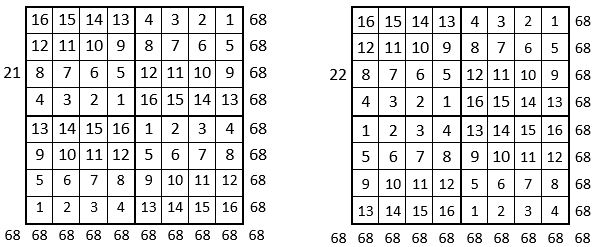
Voici ci-dessous les douze grilles « magiques » de cette première combinaison.
On peut cependant conjecturer que l’on peut tirer les mêmes conclusions, mutatis mutandis, que pour le carré naturel d’ordre n = 3 ; ce que l’on peut vérifier.
On peut sans doute opérer de la même façon, pour tout carré naturel et carré naturel alterné, de quelque ordre qu’ils soient.
On peut poursuivre l’étude de ce type d’assemblage « magique », en sélectionnant d’autres grilles comme base-départ : ainsi par exemple le Lo Shu, d’ordre n = 3 et ses 8 formes, ou bien le carré magique dit de Dürer, d’ordre n=4, et ses 8 formes ( et l’on a alors le choix parmi les 880 carrés magiques de base de la Classification de Frénicle ), ou bien encore l’un des carrés magiques de type Benjamin Franklin, d’ordre n = 8, et ses 8 formes ( très nombreux. . . ), etc . . .
Peut-on conjecturer que l’on retombe, mutatis mutandis, sur les mêmes conclusions ?
Merci à Michel Criton pour sa participation.