
Piet Mondrian (1872-1944), peintre néerlandais, pionnier de l’art abstrait, auquel il donna une de ses formulations les plus rigoureuses, à la fois comme plasticien et comme théoricien.
Pieter Cornelis Mondriaan, qui changea l’orthographe de son nom en Mondrian à Paris en 1912, est né à Amersfoort, aux Pays-Bas, le 7mars 1872. La découverte du cubisme à Paris, où il s’installa en 1912, le mit sur la voie de l’invention d’un langage pictural autonome.
Travaillant en séries, il partit de motifs progressivement épurés auxquels il appliqua la grille cubiste, considérablement simplifiée en lignes horizontales et verticales. En 1920, il créa sa première composition de lignes noires perpendiculaires, enserrant dans une grille irrégulière des plans de couleurs primaires (jaune, rouge, bleu) et de non-couleur (blanc, noir, gris). Il donna à ce nouveau langage pictural le nom de néoplasticisme, dont il théorisa les fondements dans la revue DeStijl, créée en 1917 à Leyde par Theo VanDœsburg, ainsi que dans une brochure, Le Néoplasticisme, publiée en 1920 à Paris, où il s’était réinstallé.
Maître à penser de l’avant-garde européenne, Mondrian fut inclus dans toutes les manifestations de celle-ci ; il participa notamment aux groupes Cercle et Carré puis Abstraction-Création, fondés respectivement en 1929 et 1931 à Paris. Sans abandonner ses prémisses fondatrices, le néoplasticisme n’a pas cessé d’évoluer. À partir du milieu des années 1930, Mondrian privilégia des compositions de lignes serrées, limitant le rôle de la couleur. Celle-ci revint en force dans les compositions réalisées à New-York où le peintre s’installa en 1940.
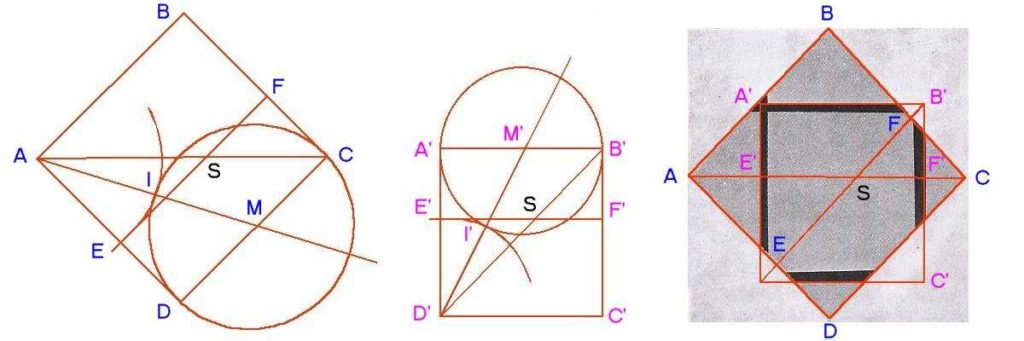
Voici le détail de la construction de la Composition : Lozenge with Four Lines and Gray
Soit le carré ABCD ; on considère le segment EF parallèle à deux côtés, qui divise le carré suivant la section doré. EF coupe la diagonale AC au point S. S divise aussi, par construction, EF et AC suivant la section dorée (Théorème de Thalès) :
SA/SC=SE/SF=(1+SQR(5)/2)=1.618
Puis Mondrian construit un second carré A’B’C’D’, de côté égal à SA, et divise ce carré en section dorée de façon analogue au premier carré ABCD.
Enfin il fait glisser ce carré A’B’C’D’ de manière que la diagonale D’B’ vienne se superposer au segment EF, les points S des deux carrés venant en coïncidence. Le segment E’F’ se superpose lui-même à la diagonale AC.
Les épaisseurs des traits dans le petit carré sont dans le rapport 3, 4, 5.
Ci dessous, Quelques visuels utilisant le style de Mondrian






















