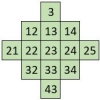
Rappel : Une Permutation figurée est toute disposition de n jetons sur les cases d’une grille carrée de n2 cases de telle sorte qu’il n’y a pas deux jetons sur une même ligne ou sur une même colonne.
Sommaire
Propriétés des grilles carrées implantées dans le carré naturel.
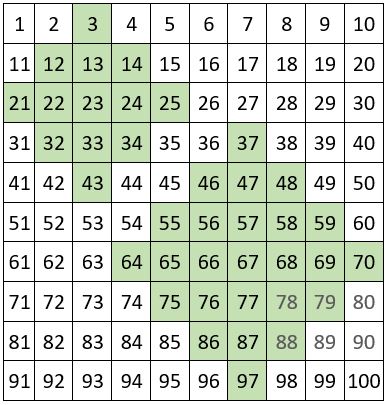
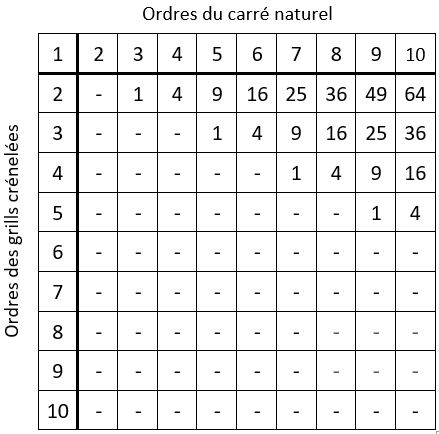
Soit par exemple le carré naturel d’ordre n = 10 de 100 cases.
On observe rapidement que les termes situés sur les permutations figurées dans chaque grille carrée, ont même somme.
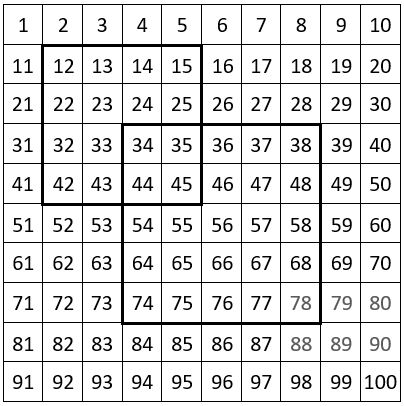
Ainsi dans la fenêtre d’ordre n = 4 de 16 cases, encadrée ci-contre, on dénombre : 4 ! = 24 permutations figurées, qui ont même somme ; soit S = 114
Dans la fenêtre d’ordre n = 5 de 25 cases, encadrée également ci-contre, les 120 permutations figurées ont la même somme, soit S = 280
Cette propriété surprenante mérite d’être examinée avec toute notre attention.
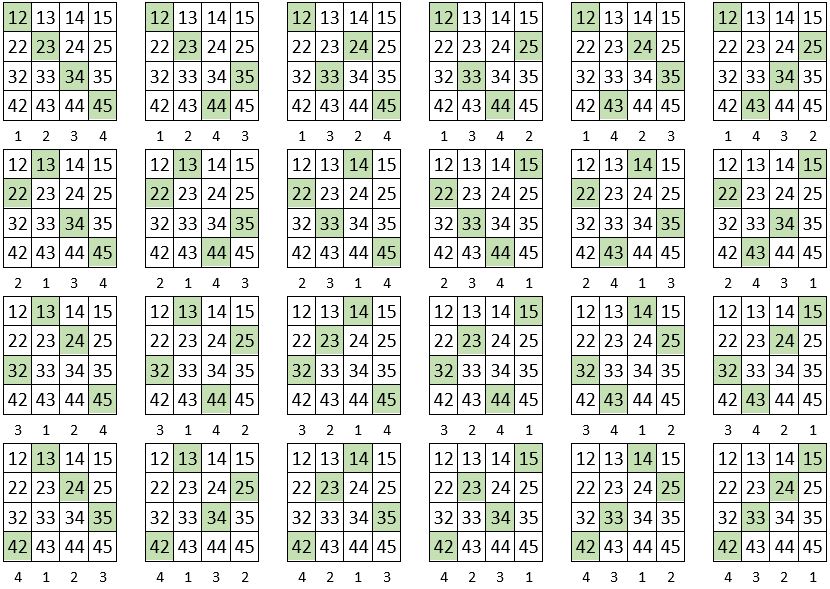
Voici, à titre de contrôle, les 24 permutations figurées de même somme, soit S = 114, dans la grille d’ordre n = 4, encadrée dans le carré naturel d’ordre n = 10 ci-dessus :
Voici le tableau numérique des 24 permutations figurées d’ordre n = 4 de même somme :
| 12 + 23 + 34 + 45 = 114 | 22 + 13 + 34 + 45 = 114 | 32 + 13 + 24 + 45 = 114 | 42 + 13 + 24 + 35 = 114 |
| 12 + 23 + 44 + 35 = 114 | 22 + 13 + 44 + 15 = 114 | 32 + 13 + 44 + 25 = 114 | 42 + 13 + 34 + 25 = 114 |
| 12 + 33 + 24 + 45 = 114 | 22 + 33 + 14 + 45 = 114 | 32 + 23 + 14 + 45 = 114 | 42 + 23 + 14 + 35 = 114 |
| 12 + 33 + 44 + 25 = 114 | 22 + 33 + 44 + 15 = 114 | 32 + 23 + 44 + 15 = 114 | 42 + 23 + 34 + 15 = 114 |
| 12 + 43 + 24 + 35 = 114 | 22 + 43 + 14 + 35 = 114 | 32 + 43 + 14 + 25 = 114 | 42 + 33 + 14 + 25 = 114 |
| 12 + 43 + 34 + 25 = 114 | 22 + 43 + 34 + 15 = 114 | 32 + 43 + 24 + 15 = 114 | 42 + 33 + 24 + 15 = 114 |
Le dénombrement des fenêtres carrées qu’il est possible de placer dans le carré naturel se présente alors ainsi dans le tableau ci-contre, l’ordre du carré naturel et l’ordre des fenêtres carrées étant limités à n = 10.
Au total, dans ce cas particulier, on compte 825 solutions.
Chaque fenêtre carrée présente sa propre constante magique.
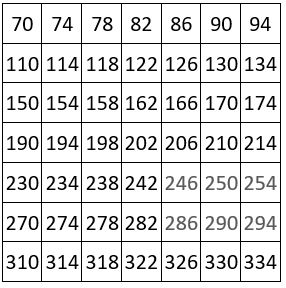
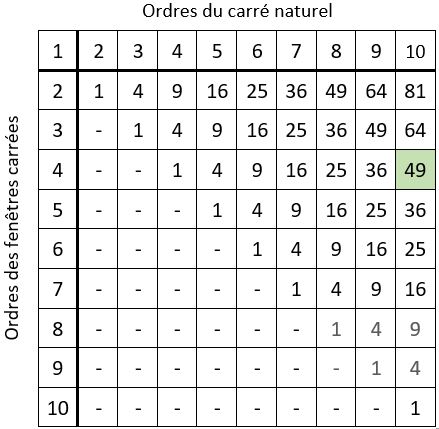
Ainsi par exemple, voici dans le tableau ci-contre, les 49 constantes magiques différentes des 49 fenêtres carrées d’ordre n = 4, prises dans le carré naturel d’ordre n = 10. Ces constantes magiques sont en progression arithmétique, de raison r1= 4 dans les lignes, et de raison r2 = 40 dans les colonnes.
Propriété générale
Si l’on sélectionne la grille carrée d’ordre n = 10, celle-ci remplit tout le carré naturel de même ordre n = 10 ; et coïncide exactement avec ce carré naturel de même ordre ; c’est une évidence.
Dans cette grille, on dénombre alors
N10 = 10 ! = 3 628 800 permutations figurées, qui ont toutes la même somme, soit S10 = 505, somme prise sur la première diagonale centrale. On peut ainsi dire dans le carré naturel d’ordre n = 10, toutes les permutations figurées ont la même somme.
C’est une propriété générale : Dans tout carré naturel, les permutations figurées ont toutes la même somme.
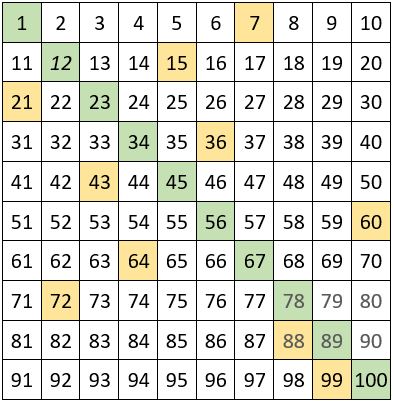
On remarque alors que les termes de cette première diagonale centrale correspondent à une progression arithmétique de premier terme a = 1, de raison r = 11 et de nombre de termes n = 10.
La somme Sn des n premiers termes de la progression arithmétique de premier terme « a » et de raison « r » est donnée par la relation générale bien connue :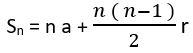
Avec a = 1 et r = n + 1 ; cette relation devient : 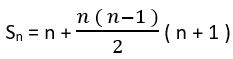
Application : n = 10 : 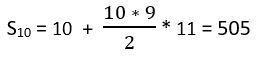
En application de cette relation, on peut alors dresser le tableau des constantes des carrés naturels ; on observe que ces constantes correspondent aux Constantes magiques du carré magique normal de même ordre :
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Constantes | 5 | 15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 |
D’autres propriétés dans le carré naturel.
On peut caler ou placer dans le carré naturel des figures crénelées qui présentent des propriétés intéressantes.
Restons avec le carré naturel d’ordre n = 10 de 100 cases, comme carré naturel de base, pris comme exemple.
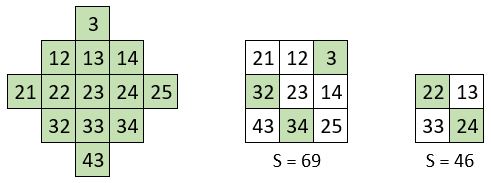
Voici ci-contre deux exemples de figures crénelées, placées dans le carré naturel d’ordre n = 10.
Ces figures apparaissent comme la superposition de deux grilles carrées imbriquées.
On dénombre 36 figures crénelées d’ordre n = 3 dans le carré naturel d’ordre n = 10. Dans chaque figure, chacune des deux grilles imbriquées présente sa propre constante magique.
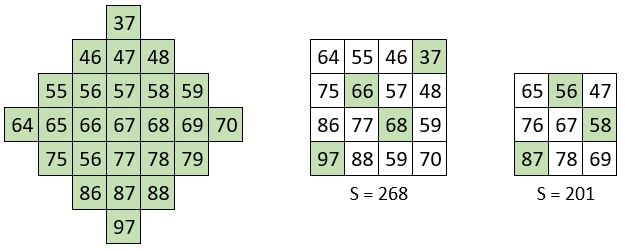
On dénombre 16 figures crénelées d’ordre n = 4 dans le carré naturel d’ordre n = 10.
On peut alors énoncer, que dans chacun de ces deux exemples, que dans chacune des deux grilles carrées imbriquées correspondantes, les permutations figurées ont la même somme.
Le dénombrement des grilles crénelées qu’il est possible de placer dans le carré naturel, se présente alors ainsi dans le tableau ci-contre, l’ordre du carré naturel et l’ordre des grilles crénelées étant limités à n = 10.
Au total, dans ce cas particulier, on compte 330 solutions. On peut bien sûr établir un tel dénombrement en prenant pour base un carré naturel d’un ordre choisi.
Cette propriété des permutations figurées, comme la précédente, apparait dans tout carré naturel, quelle que soit la parité de son ordre.
Une construction des carrés magiques
Soit la sélection d’une fenêtre d’ordre n = 4 dans le carré naturel d’ordre n = 10, affiché au début de l’article
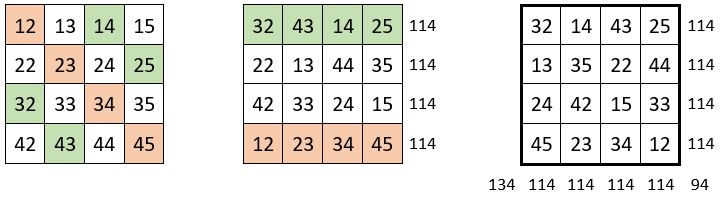
Dans les lignes la grille d’ordre n = 4, on place quatre permutations figurées d’ordre n = 4, qui remplissent toute la grille, soit dans cet exemple, les deux diagonales centrales, et les deux permutations figurées symétriques par rapport au centre de la grille ; ceci dans un ordre quelconque des lignes, qui sont ainsi magiques.
On rend magiques les colonnes, à l’aide de la Méthode classique des permutations dans les lignes.
On obtient un carré semi-magique de Constante magique M’4 = 114 ; les diagonales centrales ne sont pas magiques.
On peut regrouper par quatre les permutations figurées dans six grilles, d’où six solutions théoriques à notre problème, pour n = 4. Il y a plusieurs regroupements possibles. Je dis théoriques, car il arrive que l’on ne puisse pas rendre magique les colonnes . . .
Bien sûr, il y a d’autres solutions, pour une grille d’ordre n = 4 dans le carré naturel d’ordre n = 10 de 100 cases : rappelons que l’on peut en effet sélectionner : 7 x 7 = 49 grilles d’ordre n = 4 comme catalyseur.
Une autre méthode
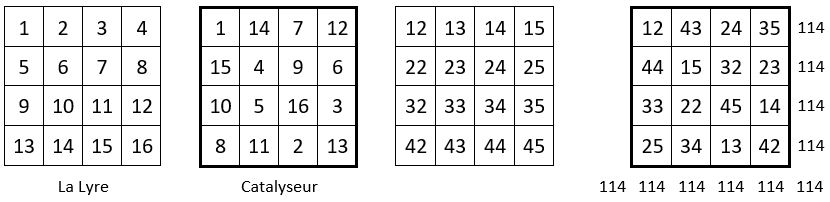
On sélectionne un carré magique de même ordre comme catalyseur.
On redistribue les termes de la fenêtre d’ordre n = 4, conformément au schéma des termes du catalyseur.
On obtient un carré magique dans les lignes, les colonnes et les deux diagonales centrales, de Cte magique M’4 = 114.
Il y a autant de solutions que de catalyseurs, soit dans ce cas particulier, les 880 carrés magiques d’ordre n = 4 de base de la Classification de Frénicle.
Conclusion
On peut ainsi conclure que les permutations figurées se cachent ainsi souvent et en très grand nombre, dans des figures dans lesquelles on est loin de soupçonner leur présence !