Les permutations figurées ont été introduites en 1883 par le mathématicien Édouard Lucas. Elles consistent en une disposition de n cases noires dans un carré n × n de sorte à constituer un carré latin (chaque ligne et chaque colonne ne contient qu’une case noire, comme n tours placées sur un échiquier de sorte que deux quelconques d’entre elles ne soient jamais en prise).
Cet article vient en complément du livre récemment paru : René Descombes – A la recherche des permutations figurées – (Amazon)
Sommaire
Les permutations figurées dans la table d’addition.
Considérons tout d’abord, la table d’addition classique, dite de Pythagore ; c’est la table d’ordre n = 10 que l’on utilise dans l’enseignement primaire pour apprendre aux enfants l’addition de dix premiers entiers.
Soit ci-dessous la table d’addition d’ordre n = 4.
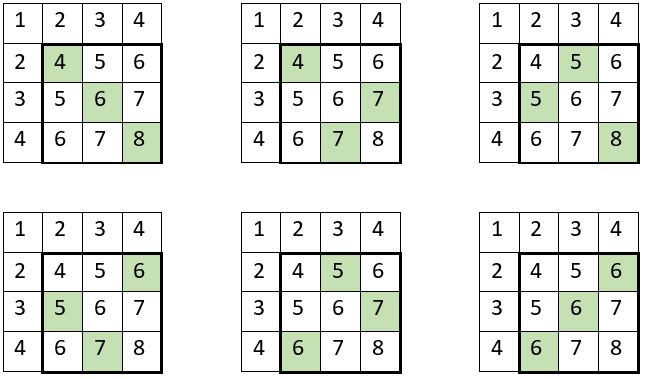
❶ On observe que la somme des termes situés sur une permutation figurée, est égale à la somme totale des facteurs d’addition, c’est-à-dire à une somme constante, S4 = 18.
Cette somme, S4 = 18 est bien égale à : ( 2 + 3 + 4 ) + ( 2 + 3 + 4 ) = 18.
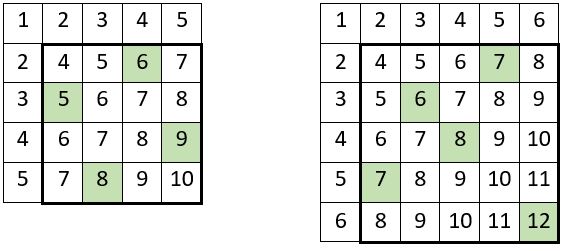
On vérifie cette propriété par exemple dans les tables ci-dessous :
dans la table d’ordre n = 5, on a : S5 = 28 ;
et dans la table d’addition d’ordre n = 6, on a : S6 = 40
❷ Dans la table d’addition classique, cette Somme Sn répond à la relation : Sn = ( n – 1 ) ( n + 2 )
On peut alors dresser le tableau ci-dessous de la Série des Sommes « Sn » : cette Série est cataloguée sous le n° A028552 dans l’OEIS ( On-Line Encyclopedia of Integer Sequences ) et présente bien d’autres propriétés.

❸ Une généralisation
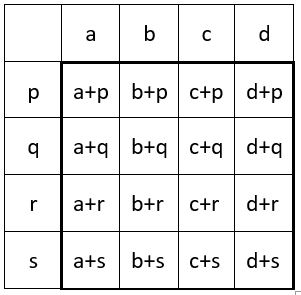
Considérons maintenant une présentation générale de la table d’addition, par exemple avec une table d’addition d’ordre n = 4. La propriété énoncée ci-dessus apparait nettement en particulier dans les deux diagonales centrales.
Dans d’application numérique ci-dessous, une table d’addition quelconque d’ordre n = 4, la constante d’addition est : S’4 = 105. On le vérifie aisément. Bien sûr la relation Sn = f ( n ) ne s’applique pas.
Les permutations figurées dans la table de multiplication.
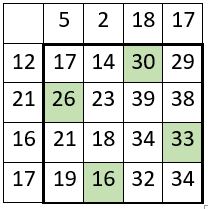
On procède de la même manière, mutatis mutandis, que pour la table d’addition ci-dessus, avec pour exemple une table de multiplication classique d’ordre n = 4.
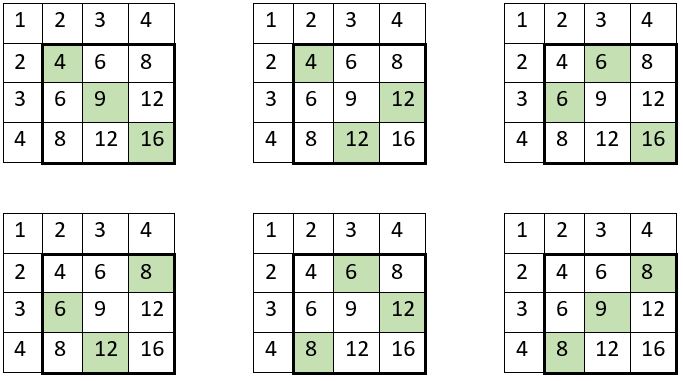
❶ Dans la grille encadrée des produits, on observe que les produits des termes situés sur une permutation figurée est constant, et égale au produit des facteurs de multiplication, soit P4 = 576.
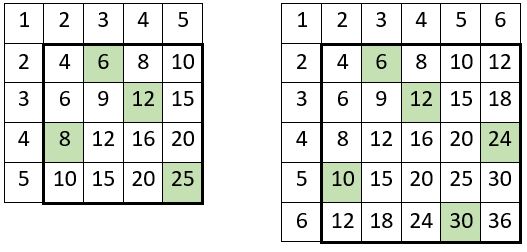
On le vérifie dans les tables ci-dessous, à titre d’exemples : P5 = 14400, et P6 = 518400
❷ Les produits Pn de la table de multiplication classique répondent à la relation : Pn = ( n ! )2
Le tableau ci-dessous rassemble quelques valeurs de ce produit Pn en fonction de l’ordre « n » de la table de multiplication correspondante; on est rapidement confronté à de grands nombres ; cette Série est répertoriée dans l’OEIS ( On-Line Encyclopedia of Integer Sequences ) sous le n° A001044.

❸ Une généralisation
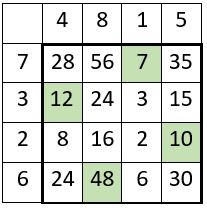
Considérons maintenant une présentation générale de la table de multiplication, par exemple avec une table d’addition d’ordre n = 4. La propriété énoncée ci-dessus apparait nettement en particulier dans les deux diagonales centrales. C’est ainsi une propriété générale des tables de multiplication.
Dans l’exemple d’application numérique, une table d’addition quelconque d’ordre n = 4, la constante de multiplication est : S’4 = 40 320. On le vérifie aisément. Bien sûr la relation Pn = f ( n ) ne s’applique pas.

▶ Édouard Lucas – Sur l’arithmétique figurative – Les permutations – Association Française pour l’Avancement des Sciences – Compte rendu de la 12e Session – Rouen – 1883
▶ René Descombes – A la recherche des permutations figurées – Amazon 2021, p.150.
