Problèmes de traversée des rivières

C’est dans un ouvrage d’Alcuin intitulé « Propositiones ad  acuendos juvenes », que l’on trouve exposé le problème « du loup, de la chèvre et du panier de choux ».

Des trois combinaisons théoriquement possibles des trois éléments « loup – chèvre –choux » pris deux à deux, seule la combinaison « loup – choux » est pratiquement possible. Le paysan n’a donc pas le choix pour sa première traversée : il traverse d’abord la chèvre, qu’il laisse sur la seconde rive, puis revient à vide prendre le panier de choux, qu’il dépose sur l’autre rive. La joie de la chèvre est de courte durée, car le paysan ramène celle-ci sur la première rive. Le loup est également frustré, car le paysan le traverse sur la seconde rive, où il reste avec le panier de choux, qui ne l’intéresse pas du tout, pendant que la paysan retourne à vide chercher la chèvre pour la ramener sur l’autre rive.
Au total le paysan effectue donc 7 traversées à force de rames, soit seul, soit avec la chèvre, le loup ou son précieux panier de choux. La barque a changé de rive en fin d’opérations. Celles-ci sont figurées de façon imagée et schématique dans les dessins successifs ci-dessous ( le panier de choux est symbolisé par un seul chou !)

En fait le problème comporte une seconde solution, légèrement différente, nécessitant également 7 traversées du paysan.
Le paysan n’a donc pas le choix pour sa première traversée : il traverse d’abord la chèvre, qu’il laisse sur la seconde rive, puis revient à vide pour emmener le loup de l’autre coté. Il ramène alors la chèvre à son point de départ. Il prends alors le choux et le transporte de l’autre coté ou il le laisse en compagnie du loup. Il revient à vide pour finalement emmener la chèvre sur l’autre rive.

Le problème posé par Alcuin peut être rendu plus compliqué, en augmentant le nombre de personnages présents ou les règles de compatibilité entre eux, et en introduisant éventuellement quelques îles sur lesquelles certains personnages peuvent être déposés temporairement. Edouard Lucas, dans ses Récréations mathématiques dans le chapitre Le jeu des traversées en bateau explique quelques cas (voir ci-dessous).

Ce genre de problème peut bien sur être résolu de manière intuitive, mais il peut également être formellement analysé par la théorie des graphes (géométrisation du problème). Dans son livre Aventures mathématiques, Miguel de Guzmán, analyse le problème des traversées à l’aide de graphes de tous les possibles.

M. et Mme Schmitt et leurs deux enfants Pierre et Marie, ainsi que le chien Bobi, ont, au cours d’une excursion, à traverser une rivière. Il n’y a pas de pont ni de passerelle à proximité. Cependant ils ont à leur disposition une barque, dont la capacité est limitée à 80 kg. M. et Mme Schmitt qui se portent bien, pèsent justement chacun 80 kg. Pierre et Marie pèsent chacun la moitié de ce poids ; et le chien Bobi, un épagneul breton, pèse une dizaine de kg.

M. Schmitt qui se souvient vaguement du problème du loup, de la chèvre et du chou, se met en devoir de faire traverser sa petite famille.

Pierre et Marie traversent. Pierre revient et laisse la barque à sa mère qui traverse. Marie ramène la barque et revient avec Pierre, qui retraverse pour laisser la barque à son père ; celui-ci rejoint son épouse. marie revient tout spécialement pour faire traverser le chien Bobi. Elle revient encore une fois pour prendre son frère Pierre. Au total 11 traversées sont nécessaires. On dressera facilement le tableau-résumé de ces opérations successives. On remarquera que les intéressés laissent toujours la barque qu’ils ont empruntée sur la rive opposée à celle où ils l’ont trouvée. Ce qui dénote un manque total de savoir-vivre; mais comment faire autrement ?

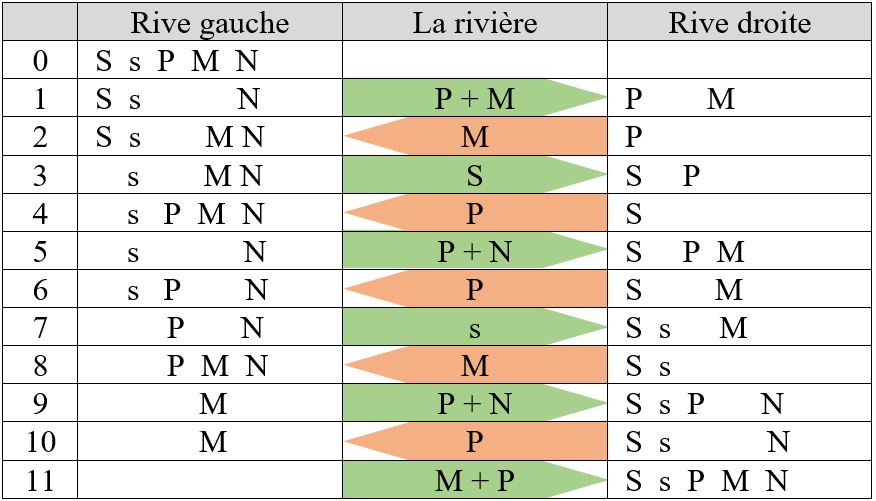
Voici un énoncé un peu différent d’un problème analogue. La Famille Schmitt est alors ainsi composée : M. Schmitt ( S = 85 kg), Mme Schmitt (s = 65kg), Pierre (P = 45 kg), Marie (M = 40 kg) et Nicole (N = 25kg). La capacité de la barque est limitée à 85 kg. Nicole, la petite sœur, ne sait pas ramer, et en raison de son jeune âge, ne doit pas rester seule sur une rive ; en outre Pierre ne peut effectuer deux traversées consécutives, trop fatigantes pour ce jeune garçon.

On trouve la solution résumée dans le tableau ci-dessous, que l’on peut facilement décoder :

Un petit détachement de soldats arrive au bord d’une rivière qu’il lui faut traverser à tout prix ; or le pont a été détruit, et il n’y a pas de gué à proximité. Que faire ?

Cependant un homme de troupe fait remarquer à l’officier qui commande le détachement, deux gamins en train de s’amuser dans une petite barque, près de la rive qu’ils abordent.. Mais la barque est tout juste assez grande pour les deux gamins ensemble, ou bien pour un seul adulte. C’est néanmoins grâce à cette frêle embarcation que tous les soldats peuvent gagner l’autre rive. Comment font-ils ?

Les deux gamins embarquent et gagnent l’autre rive. L’un d’eux débarque, et le second refait tout seul la traversée en sens inverse. Il laisse l’embarcation à un premier soldat, qui peut ainsi franchir la rivière. Le gamin resté sur l’autre rive revient avec la barque, pour reprendre son camarade, et à eux deux, ils retraversent la rivière sur leur barque. On est ramené au point de départ…Les gamins font ainsi cette astucieuse navette jusqu’à ce que tous les soldats aient franchi la rivière : on compte ainsi 5 traversées pour le passage d’un soldat ! Pauvres gamins, ils auront « bien mérité de la patrie » ! Notons qu’à l’issue de cette série de navettes, les gamins récupèrent leur petite barque sur leur rive.(d’après B. Kordiemsky, 1963)

C’est un très vieux jeu mathématique, que l’on trouve notamment dans l’ouvrage de Nicolas Chuquet (Paris 1445 – 1500) : « Inventions de nombres en général, lesquelz par la Règle des premiers, se treuvent »: la « Règle des premiers » est l’emploi de l’algèbre. Ce traité fait suite à son « Triparty en la science des nombres » (1484), dans lequel se trouvent déjà la notation cartésienne des exposants, l’emploi de ces mêmes exposants dans la résolution des équations, les signes algébriques, la règle des signes, et mêmes le germe des logarithmes ; c’est le plus ancien traité d’algèbre écrit par un français. Parmi ces « jeux et esbattements qui par la science des nombres se font », voici celui des « troys maryz ».

Trois maris jaloux accompagnés de leurs épouses, se proposent de traverser une rivière. Ils disposent d’une barque qui, comme on peut s’y attendre, ne peut embarquer que deux personnes à la fois. Or il est exclus qu’une épouse reste en compagnie d’un ou de deux hommes, si l’un d’eux n’est pas son mari !

Onze traversées sont nécessaires pour ce changement de rive. On peut schématiser le déroulement des opérations de la manière suivante : on appelle A, B, C les trois maris jaloux, et a,b,c leurs moitiés.

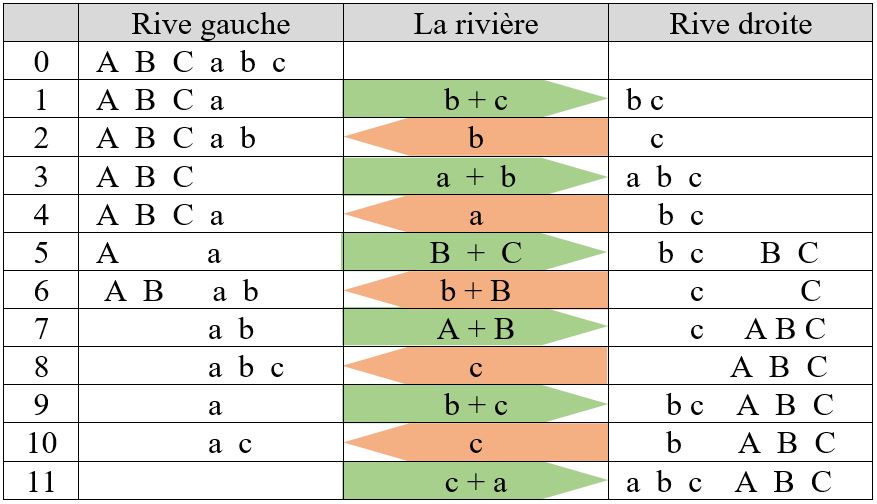
On connaît 4 solutions à ce problème, peu différentes les unes des autres.

Que se passerait-il s’il s’agissait de « 4 maris jaloux », de 4 couples se proposant de traverser une rivière dans les mêmes conditions, en particulier avec cette même barque limitée à 2 passagers ? Et bien, le problème n’a pas de solution, le transfert n’est pas possible. Par contre il devient possible si les protagonistes disposent d’une barque un peu plus grande, admettant trois passagers sans risque de couler au fond : neuf traversées sont alors nécessaires dans ce cas, comme le montre le tableau-résumé des opérations ci-dessous :

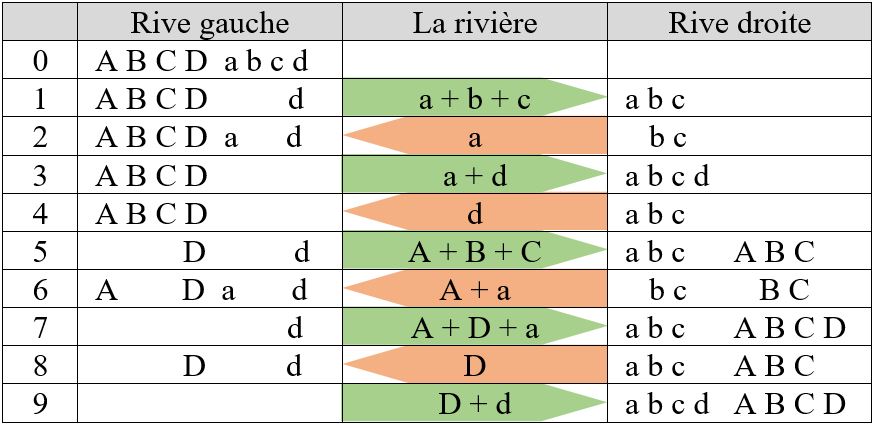
Voici maintenant une solution avec cinq maris jaloux ! La barque est toujours limitée à 3 passagers : onze traversées sont alors nécessaires dans ce cas-là

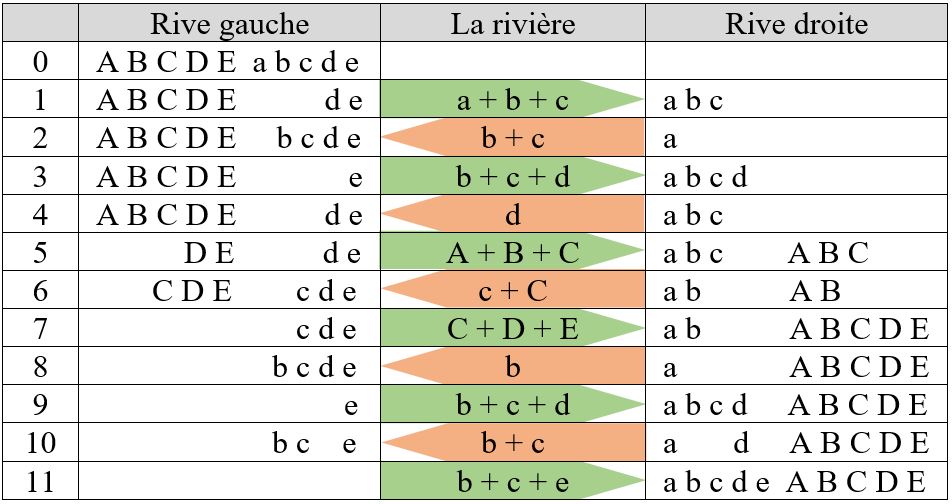
On peut généraliser le problème des maris jaloux, avec n couples.

cf. Lucas, 1891, pp. 221/222, Note I

Trois missionnaires et trois cannibales, qui se trouvent sur une rive d’une rivière, veulent rejoindre l’autre rive, à l’aide d’une barque qui ne peut admettre que deux passagers à la fois, sans risque de chavirer ( la rivière est infestée de crocodiles). Si les cannibales se trouvent plus nombreux que les missionnaires sur l’une des deux rives, les missionnaires seront tués et mangés ! Les six protagonistes peuvent-ils traverser la rivière tous sains et saufs ? S’ils le peuvent, comment y arrivent-ils avec le minimum de traversées ? On admet que tous savent ramer.

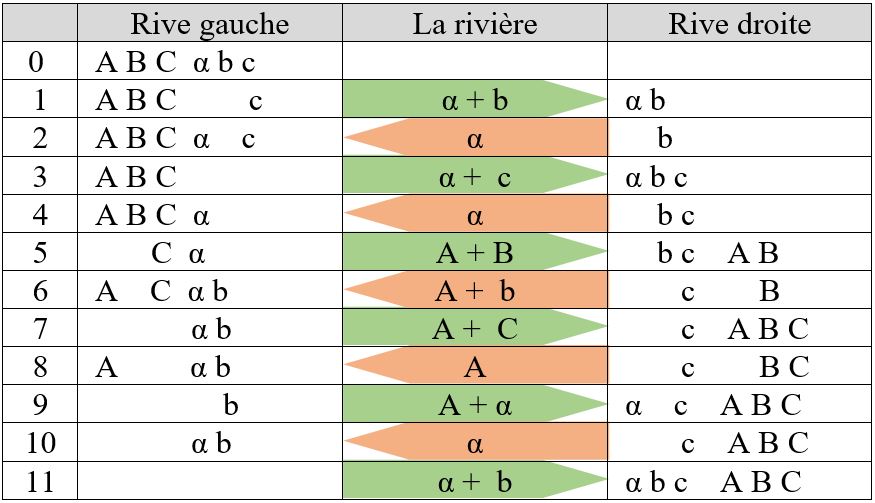
Il y a 4 solutions variantes possibles à ce problème, en 11 traversées. Si l’on appelle A, B, C les missionnaires, et a, b, c les cannibales, les solutions coïncident avec celles du problème dit des trois maris jaloux ( voir précédemment).

Il y a 4 solutions variantes possibles à ce problème, en 11 traversées. Si l’on appelle A, B, C les missionnaires, et a, b, c les cannibales, les solutions coïncident avec celles du problème dit des trois maris jaloux ( voir précédemment).

Remarque : Il n’y a pas de solution avec une barque limitée à 2 passagers pour 4 missionnaires et 4 cannibales. Mais si la barque peut admettre 3 passagers, il y a une solution en 9 traversées ( considérations analogues à celles concernant le problème des maris jaloux)

Variante : Que se passerait-il si, parmi les cannibales , il n’y avait qu’un seul d’entre eux qui sache ramer ? Cette condition supplémentaire entraînerait-elle  nécessairement des traversées supplémentaires ? On trouve une solution en 9 traversées (c’est « α » qui sait ramer, et est beaucoup à l’ouvrage): c’est la solution la plus rapide.

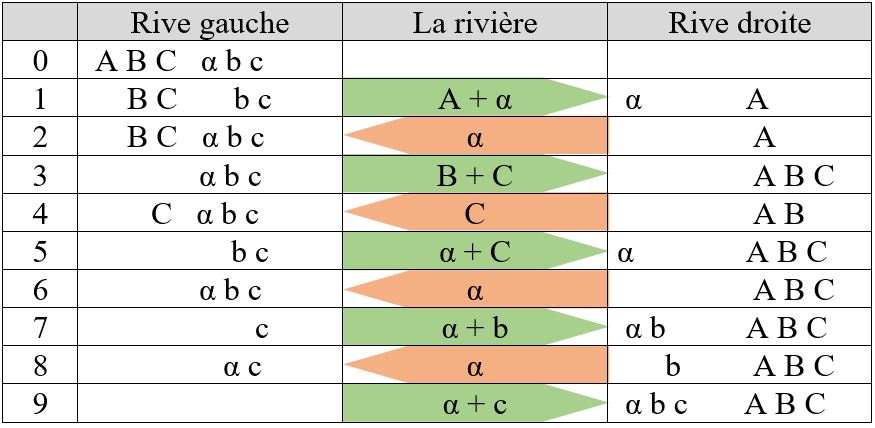
Il existe d’autres solutions, dont une en onze traversées, qui n’est pas sans intérêt  ( cf. Bruneau, 1939, pp. 94/95)

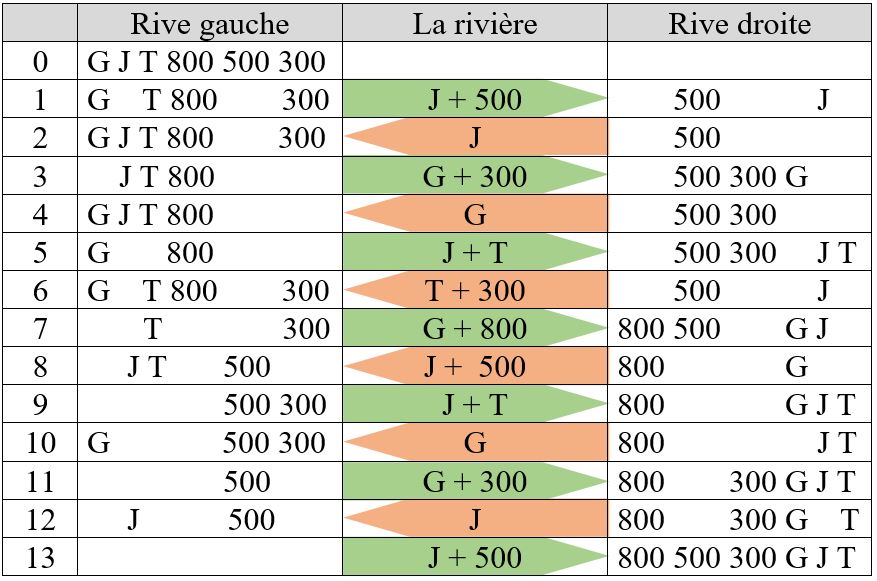
Ce problème est d’origine anglaise (Dudeney, 1958). Trois contrebandiers, dont nous conserverons les noms, ont à traverser une rivière, en l’occurrence la Tamise à mont d’Oxford, à l’aide d’une barque, avec leurs sacs de contrebande. Giles porte un sac de produits prohibés d’une valeur de 800 Livres, Jasper un sac d’une valeur de 500 Livres, et Timothy un sac d’une valeur de 300 Livres. La barque est limitée au transport de deux passagers, ou d’un passager et d’un sac, quelque soit sa valeur. Ces hommes ont si peu confiance les uns envers les autres, qu’ils n’admettent pas que l’un d’entre eux puisse rester seul sur une rive ou dans la barque avec un sac de valeur supérieure au sien propre, mais 2 contrebandiers peuvent rester ensemble avec des sacs de valeurs supérieures à leur propre sac.

Comment s’y prendront-ils pour traverser la Tamise en toute confiance ? La solution est résumée dans le tableau ci-après. Le passage de la rivière avec les contraintes imposées, nécessite 13 traversées. Personne ne reste seul sur la berge ou ne prend place dans la barque avec un sac de valeur supérieure à celle de son propre sac de marchandises. Mais aussi deux contrebandiers ne restent jamais avec des sacs dont les valeurs ajoutées forment un total supérieur à la valeur de leurs propres sacs ; ce qui est plus que n’en demande l’énoncé du problème !

C’est une variante du problème des maris jaloux. Les quatre filles du colonel, dont la trop sévère éducation était devenue intolérable,  décident un jour de s’enfuir, c’est-à-dire de gagner l’autre rive de la rivière qui longe la propriété du colonel, où des amis peuvent les accueillir.

Elles mettent leurs fiancés dans la confidence, mais ne disposent pour franchir la rivière, que d’une petite embarcation limitée à deux passagers ; de plus les fiancés sont si jaloux, qu’aucun ne tolère la compagnie de sa fiancée avec un autre homme, s’il n’est lui-même présent !

On sait que le problème est insoluble avec une barque à 2 passagers. Cependant une petite île providentielle se trouve justement au droit de la propriété du colonel, laquelle va permettre la fuite des quatre filles, en respectant les contraintes indiquées ci-dessus. Cette île est disposée en effet de façon à faire étape, ou de passer au large de l’île.

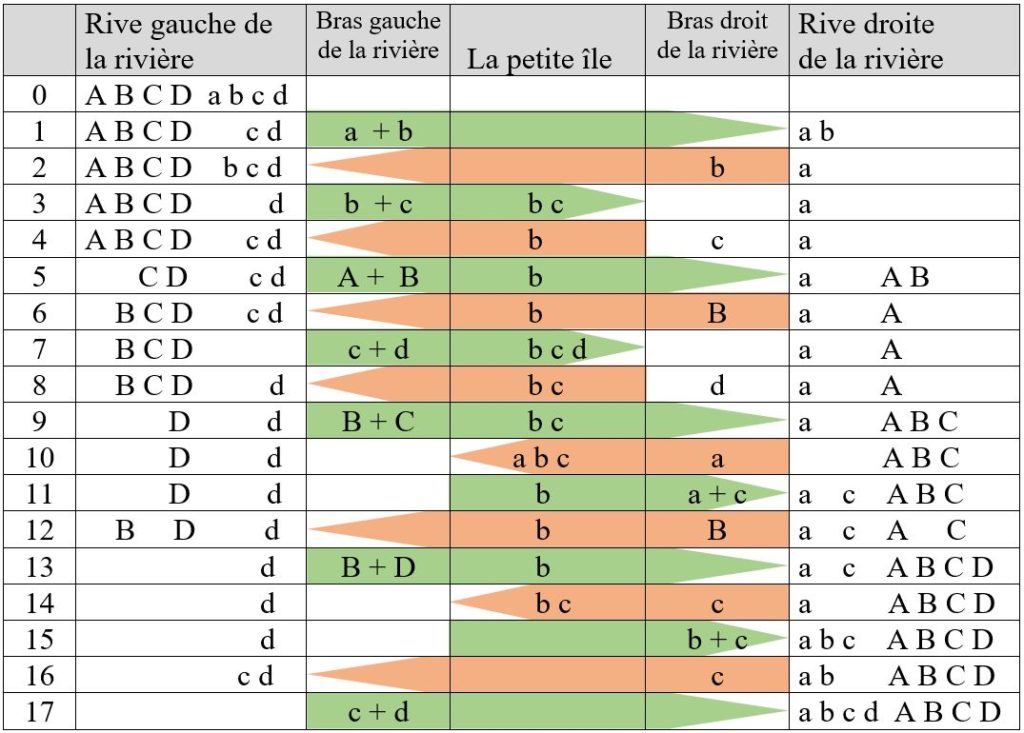
Désignons par A, B, C, et D les 4 fiancés jaloux, et par a, b, c, et d  les quatre filles du colonel. Le tableau ci-dessous résume les 17 traversées nécessaires dans cette solution (il y en a plusieurs).

Le trajet de la barque est matérialisé par les flèches colorées.

(D’après Dudeney, 1958)

A la traditionnelle barque pourrait être substitué un bac ou un téléphérique : le rôle du  passeur, ou du préposé à la cabine – elle aussi très petite – étant dévolu à l’un des protagonistes, le problème des rameurs ne se posant plus. On peut naturellement franchir une rivière par une passerelle ou un pont …

Parmi les « problèmes de pont », rappelons le célèbre « Problème des Sept Ponts de Koenigsberg » (Koenigsberg, aujourd’hui Kaliningrad en Lituanie, sur la Pregel, ancienne capitale de la Prusse-Orientale), exposé pour la première fois, semble-t-il, par Leonhard Euler, dans un Mémoire de 1759 qui a pour titre : « Solutio problematis ad Geometriam situs pertinentis ».

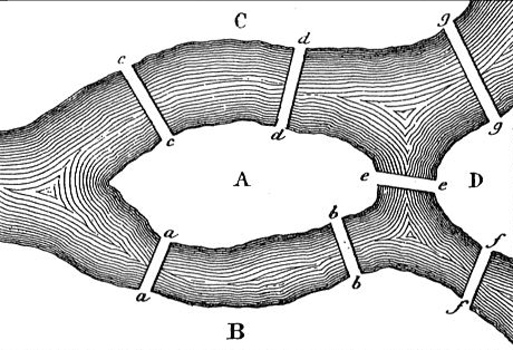
Il s’agit de trouver un itinéraire tel que l’on passe sur chaque pont, et que l’on n’y passe qu’une seule fois (autrement dit les sept ponts sont à sens unique). Leonhard Euler a démontré que le problème n’a pas de solution. Ce genre de circuit a gardé le nom de « Circuit eulérien ».

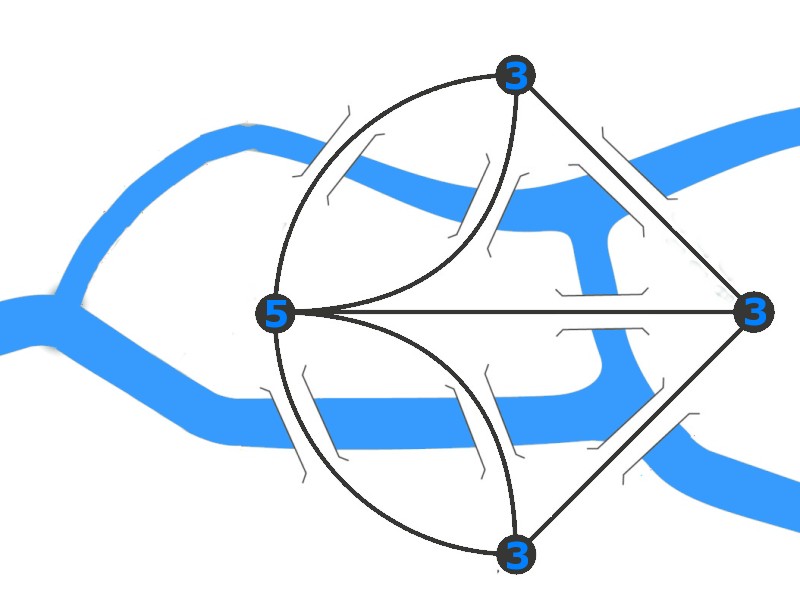
Chaque arrête du graphe représente un pont à traverser.
Chaque nœud du graphe représente une section territoriale. Le degré de chaque nœud est le nombre d’arêtes qui lui sont reliées.
Dans le cas de Koenigsberg, tous nœuds ont des degrés impairs .
Euler a démontré que, pour qu’un trajet passe une fois et une seule sur chaque arête et revienne au point de départ, il est nécessaire que tous les nœuds du graphe soient reliés à un nombre pair d’arête.