Dans toute suite numérique en progression arithmétique, on peut toujours assembler en carré magique par addition d’ordre n, n2 termes consécutifs.
Certaines progressions arithmétiques génèrent des carrés magiques par addition, intéressants par leur composition, que nous nous proposons de présenter, de préciser et de développer.
Sommaire
Le carré magique normal.
Tout d’abord, on qualifie de normal le carré magique d’ordre n, dont les n2 termes sont les n2 premiers nombres entiers.
Exemple ci-contre :
La Lyre correspond au carré naturel de même ordre.
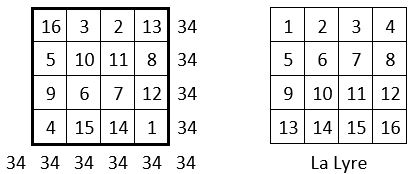
Les nombres de la suite des termes de ce carré magique, ou de la Lyre correspondante, sont en progression arithmétique de premier terme a = 1 et de raison r = 1 : c’est la plus simple progression arithmétique qui présente la propriété générale énoncée ci-dessus.
Des nombres impairement pairs.
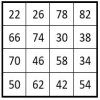
On qualifie d’impairement pair, tout nombre pair divisible seulement une fois par deux.
Ainsi n = 6 est le premier et le plus petit nombre impairement pair de cette suite :
6, 10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62, . . .
Cette suite correspond à une progression arithmétique de premier terme a = 6 et de raison r = 4.

En application de la propriété générale énoncée ci-dessus, on peut ainsi assembler en carré magique, avec l’aide d’un catalyseur, toute série de n2 nombres consécutifs impairement pairs pris dans la suite naturelle des nombres impairement pairs. Exemple pour n2 = 16 ( en gras ci-dessus ) :
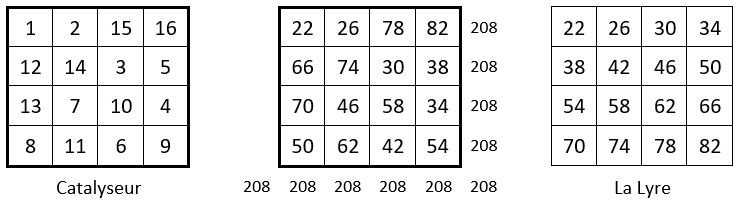
Ce carré magique est un carré magique à quartiers opposés égaux ( ci-contre ) Cette suite génère ainsi une infinité de carrés magiques, de diverses Constantes magiques.
Une suite de sous-carrés de quatre cases.
Considérons maintenant, dans la suite naturelle des entiers, la suite indéfinie des séquences successives de 4 termes successifs assemblés en carré, ainsi que la somme de ces 4 termes :
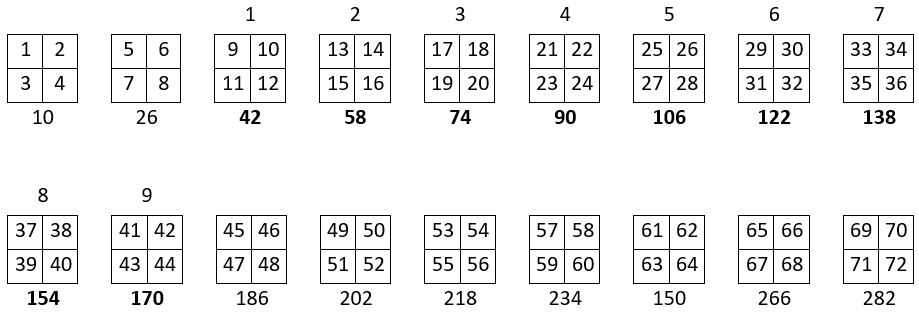
Les sommes de ces sous-carrés de 4 cases, se succèdent dans le cadre d’une progression arithmétique de premier terme a = 10, et de raison r = 16 = 42
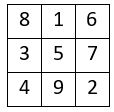
On se propose alors d’assembler en carré, une sous-série de n2 = 9 termes consécutifs pris dans cette suite de sommes, et assemblés conformément à l’une des huit formes du Lo Shu, pris comme catalyseur :
42, 58, 74, 90, 106, 122, 138, 154, 170
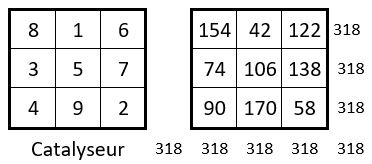
On obtient un carré magique d’ordre n = 3, de Constante magique M’3 = 318.
On remarque que : 318 = 106 x 3
On compte au moins huit solutions pour chaque choix de
n2 = 9 termes consécutifs.
Suite normale issue du carré naturel d’ordre n = 3.
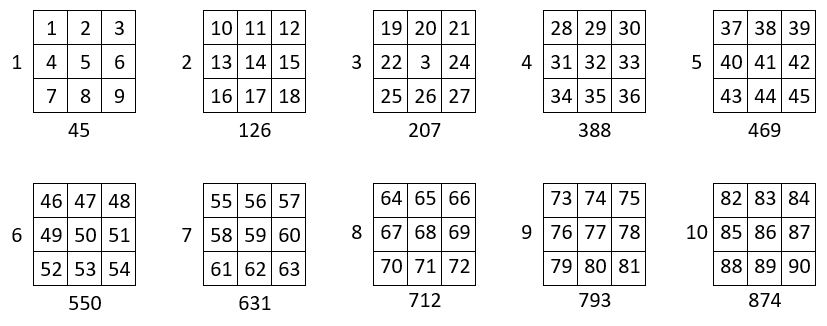
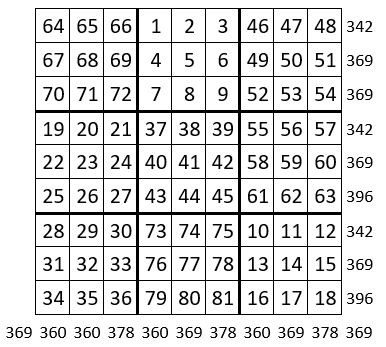
On sélectionne les n2 = 9 premiers carrés de cette suite, que l’on assemble en carrés formateurs, dans une grille d’ordre n = 9, avec la participation de l’une des formes du Lo Shu pris comme catalyseur ( ci-contre ) : on obtient bien ainsi une grille normale, contenant les 92 = 81 premiers entiers consécutifs ( ci-dessous )
Cette grille n’est pas magique, mises à part quelques lignes et quelques colonnes, ainsi que les deux diagonales centrales, qui totalisent M9 = 369, soit la Constante magique du carré magique normal d’ordre n = 9
Cette grille n’est cependant pas sans intérêt.
Les cases homologues dans chacun des carrés formateurs, forment un carré magique d’ordre n = 3 : on obtient ainsi neuf carrés magiques de constantes magiques diverses (ci-dessous )
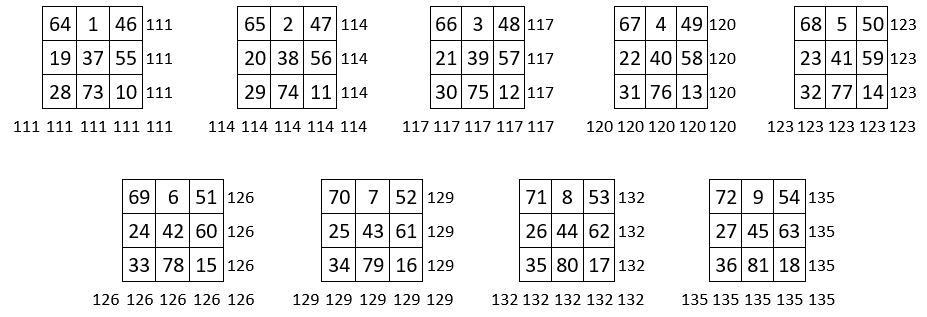
Les Constantes magiques de ces 9 carrés magiques sont en progression arithmétique, de premier terme a = 111 et de raison r = 3 :
111, 114, 117, 120, 123, 126, 129, 132, 135
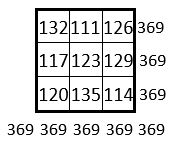
Ce qui permet de les assembler en carré magique, avec l’aide du Lo Shu ! :
On peut enfin assembler en carré magique, les sommes des termes de ces carrés formateurs, avec toujours la participation de l’une des formes du Lo Shu infatigable, pris comme catalyseur (ci-contre)
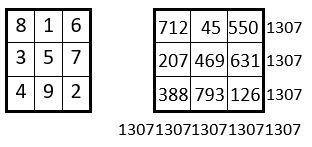
On pourrait bien sûr choisir une série quelconque de n2 termes consécutifs, pris dans la suite issue du carré naturel d’ordre n = 3, dont nous avons donné les dix premiers termes, avec leur somme.
Remarques à propos des progressions géométriques.
A l’instar des progressions arithmétiques, les progressions géométriques génèrent des carrés magiques, mais des carrés magiques par multiplication.
On peut alors paraphraser la propriété énoncée au début de ces pages, concernant les progressions arithmétiques :
Dans toute suite numérique en progression géométrique, on peut toujours assembler en carré magique multiplicatif d’ordre n, n2 termes consécutifs.
Donnons un exemple.

Soit la progression géométrique de premier terme a = 1, et de facteur multiplicatif m = 2.
On sélectionne par exemple n2 = 9 termes consécutifs dans cette suite (en gras ci-dessus), que l’on place dans une grille d’ordre n = 3 de 9 cases, conformément à la polygraphie d’un carré magique par multiplication de même ordre, pris comme catalyseur, de Constante magique multiplicative MM3 = 4 096.
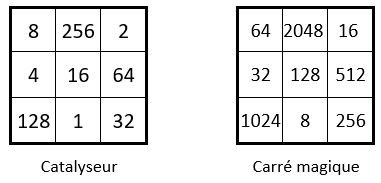
Le carré numérique obtenu, est un carré magique par multiplication, dans les lignes, les colonnes et les deux diagonales centrales, de Constante magique multiplicative MM’3 = 2 097 152.
Une difficulté dans cette construction, c’est la recherche d’un catalyseur, ce qui n’est pas toujours évident, pour n > 3.
Comme pour les progressions arithmétiques, les progressions géométriques génèrent un nombre infini de solutions ; on arrive vite à des termes constitués de très grands nombres.