Sommaire
Arnaut Daniel
La Sextine est une structure poétique particulière inventée par le troubadour provençal du Moyen Age Arnaut Daniel ( 1150 – 1210 ).

Arnaut Daniel fut certainement parmi les troubadours et les trouvères, l’un des plus habiles artisans de l’ancien provençal, le meilleur forgeron de sa langue maternelle, nous dit Dante lui-même dans le Purgatoire.
Pétrarque aussi lui vouait un profond respect, l’appelant le gran maestro d’amore (le grand maître d’amour chevaleresque).
Arnaud Daniel est né au château de Riberac, en Dordogne ; on a peu d’informations sur sa vie et ses activités. On dispose actuellement de dix-huit de ses poèmes, dont une seule version de la Sextine.
La Sextine se compose de six strophes de six vers, dont chacun se termine par un mot-rime, qui reparait diversement distribué dans les vers de toutes les strophes, le dernier mot-rime d’une strophe devenant le dernier mot-rime de la première ligne de la strophe suivante. Et de la dernière strophe, on revient à la première.
Une ultime strophe de trois vers, nommée Tornada, reprend les six mots-rimes.
La Sextine originale d’Arnaut Daniel, la seule que l’on connaisse, est écrite en langue provençale ancienne (XIIème siècle), peu compréhensible pour un homme d’aujourd’hui. Voici la version originale et une traduction en français contemporain due à Jacques Roubaud, dans laquelle apparaissent bien la structure de ce poème et ses contraintes : cette sextine est intitulée La Sextine d’ongle et oncle :
Lo ferm voler qu’el cor m’intra
no-m pot ges bècs escoissendre ni ongla
de lauzangier qui pert per mal dir s’arma
e car non l’aus batr’ab ram ni ab verga
sivals a fra lai on non aurai oncle
jauzirai joi en vergier o dinz cambra
Quan mi soven de la cambra
on a mon dan sai que nuills hom non intra
anz me son tuich plus que fraire ni oncle
non ai membre no-m fremisca neis l’ongla
aissi uom fai l’enfas denant la verga
tal paor ai no-l sia trop de l’arma
Del cors li fos non de l’arma
e cossentis m’a celat dinz sa cambra
que plus mi nafra-l cor que colps de verga
car lo sieus sers lai on ill es non intra
totz temps serai ab lieis cum carns et ongla
e non creirai chastic d’amic ni d’oncle
Anc la seror de mon oncle
non amei plus ni tant per aquest’arma
c’aitant vezis com es lo detz de l’ongla
s’a liei plagués volgr’esser de sa cambra
de mi pot far l’amors qu’inz el cor m’intra
miells a son vol qu’om fortz de frévol verga
Pois flori la seca verga
ni d’En Adam mogron nebot ni oncle
tant fin’amors com cela qu’el cor m’intra
non cuig fos anc en cors ni eis en arma
on qu’ill estei fors en platz o dins cambra
mos cors no-is part de lieis tant com ten l’ongla
C’aissi s’enpren e s’en ongla
mos cors en lei com l’escorss’ en la verga
q’ill m’es de joi tors e palaitz e cambra
e non am tant fraire paren ni oncle
q’en paradis n’aura doble joi m’arma
si ja null hom per ben amar lai intra
Tornada
Arnautz tramet sa chansson d’ongl’e d’oncle
agrat de lieis que de sa verg’a a l’arma
son Desirat cui pretz en cambra intra
La ferme volonté qui au cœur m’entre
ne peut ni langue la briser ni ongle
de médisant qui perd à mal dire son âme
n’osant le battre de rameau ni de verge
sinon en fraude là où je n’ai nul oncle
je jouirai de ma joie en verger ou chambre
je me souviens de la chambre
où pour mon mal je sais que nul homme n’entre
mais tous me sont pires que frère ou qu’oncle
tremblent tous mes membres jusqu’à l’ongle
ainsi que fait l’enfant devant la verge
tant j’ai peur de n’être assez sien dans mon âme
Ah que je sois sien dans le corps non dans l’âme
et qu’elle m’accueille en secret dans sa chambre
plus me blesse le cœur que coup de verge
d’être son serf qui là où elle est n’entre
toujours je serai près d’elle comme chair et ongle
n’écoutant aucun reproche d’ami ni oncle
Jamais la sœur de mon oncle
je n’aimerai tant ou plus par mon âme
aussi proche qu’est le doigt de l’ongle
s’il lui plaisait je voudrais être da sa chambre
il peut faire de moi l’amour qui en mon cœur entre
a mon gré comme homme un fort de faible verge
Depuis qu’a fleuri le sèche verge
que du seigneur Adam sont nés neveu et oncle
un amour qui comme celui qui dans mon cœur entre
je ne crois qu’il a été en corps ni âme
où qu’elle soit sur la pace ou dans la chambre
mon cœur sera moins loin que l’épaisseur d’un ongle
Qu’ainsi s’enracine devienne ongle
mon cœur en elle comme écorce en la verge
elle m’est de joie tour et palais et chambre
je n’aime tant frère parent ni oncle
en paradis aura double joie mon âme
si jamais homme, d’avoir aimé y entre
Tornada
Arnaut envoie sa chanson d’ongle et d’oncle
Pour plaire à celle qui de sa verge à l’âme
Son Désiré son prix entre sa chambre.
La Méthode de la Spirale
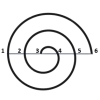
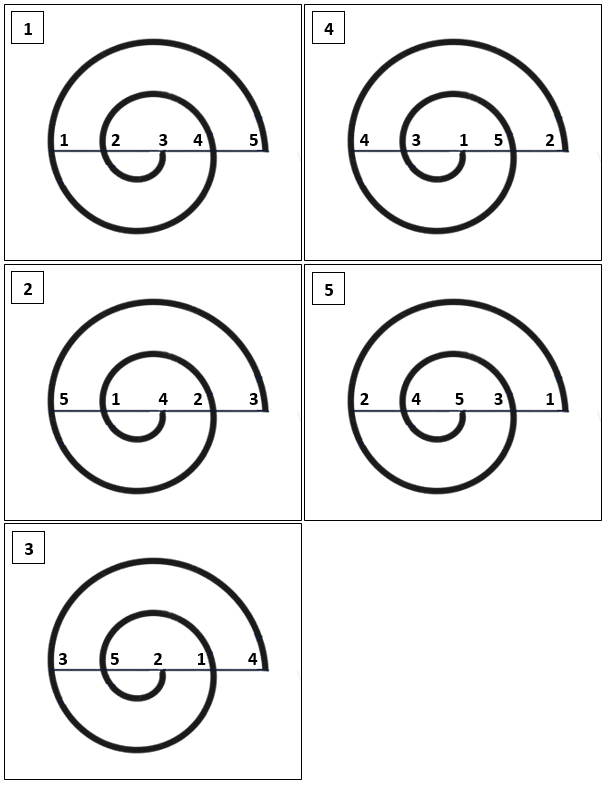
La place des mots-rimes dans chaque strophe résulte d’une permutation, qui est toujours la même, et que l’on peut représenter dans une spirale de la façon suivante ( Voir ci-dessous) :
On numérote les mots-rimes : 1, 2, 3, 4, 5, 6.
On place ces six premiers entiers sur l’axe horizontal d’une spirale, correspondant à la première strophe de la Sextine ( 1 )
On lit alors ces chiffres dans l’ordre de la spirale : 6, 1, 5, 2, 4, 3 , ce qui correspond au placement des mots-rimes dans la seconde strophe de la Sextine ( 2 )
On procède de la même façon, successivement, pour les strophes suivantes, jusqu’à la sixième strophe.
On remarque que si l’on poursuit la manip une septième fois, on retombe sur le placement initial des mots-rimes.
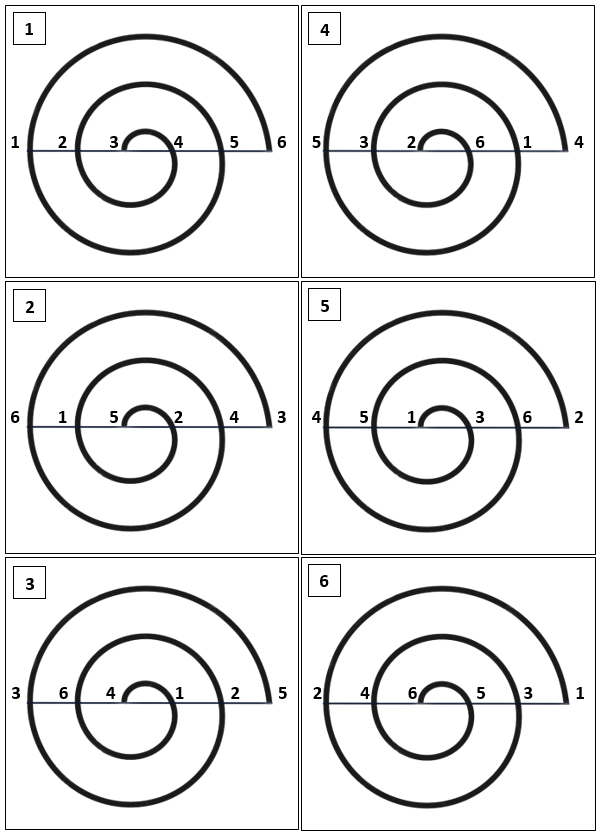
Les mots-rimes numérotés mis successivement en colonnes dans une grille d’ordre n = 6 de 36 cases, forment un carré latin, non diagonal.
Et comme dans tout carré latin, les termes homologues de la Sextine sont situés sur une permutation figurée.
La Quenine de Raymond Queneau
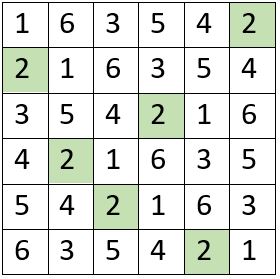
Sur le modèle de la Sextine d’Arnaut Daniel, Raymond Queneau a imaginé la structure de la Quenine, représentée dans la Planche ci-dessous, avec le carré latin correspondant, ci-contre. On trouve des exemples de la Quenine dans l’Anthologie de l’Oulipo – 2009.
Et comme dans tout carré latin, les termes homologues de la Quenine sont situés sur une permutation figurée.
Les nombres de Queneau
La Méthode de la spirale ne peut pas être généralisée à tout ordre n, pour former une n-nine . . .
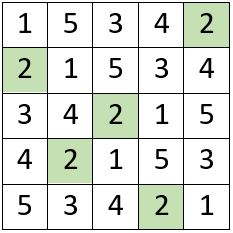
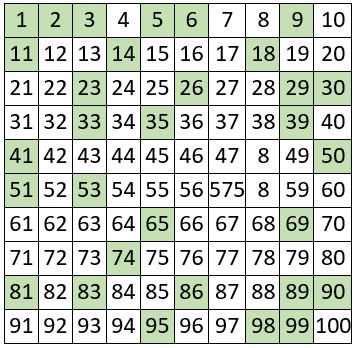
On démontre en effet, qu’on ne peut fabriquer de manière effective des quenines que pour les nombres n tels que « 2n + 1 » est un nombre premier ( Jean Guillaume Dumas 2008 )
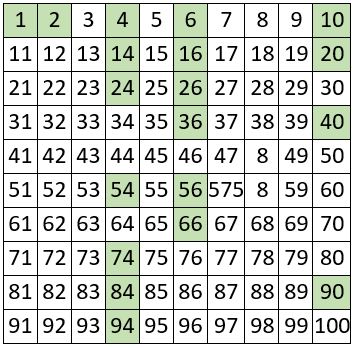
Voici les 31 nombres « n » tels que « 2n + 1 » est un nombre premier, inférieurs à 100, pochés dans un « Crible d’Eratosthène » : Ces nombres sont appelés Nombres de Queneau.
Quant au nombre correspondant « 2n + 1 », il est nommé Nombre premier sûr.
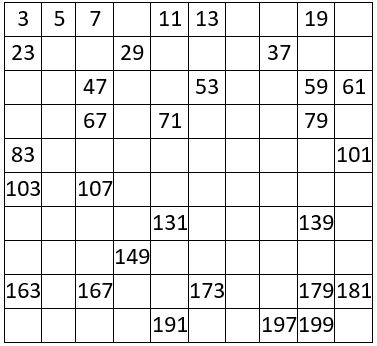
Au moins 37% des entiers n, tels que « 2n+1 » soit premier, sont des Nombres de Queneau : c’est la Conjecture de Emil Artin ( 1927 ) ; et l’on conjecture qu’il y a une infinité de Nombres de Queneau.
Jean Guillaume Dumas 2008, donne dans son étude, les Nombres de Queneau inférieurs à 1000.
Dans la Série A054639 de l’OEIS, On-Line Encyclopedia of Integer Sequences, de Sloane, on trouve également une suite de Nombres de Queneau.
Les nombres de Sophie Germain
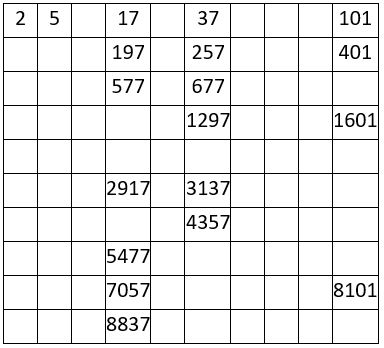
Lorsqu’un Nombre de Queneau est lui-même un nombre premier, on dit que c’est un Nombre de Sophie Germain ; autrement dit, tous les Nombres de Sophie Germain sont des Nombres de Queneau. Voici 36 Nombres de Sophie Germain inférieurs à 1 000, avec les Nombres premiers sûrs ( 2n + 1 ) qui leur correspondent ( Voir la Série A005384 de l’OEIS ).
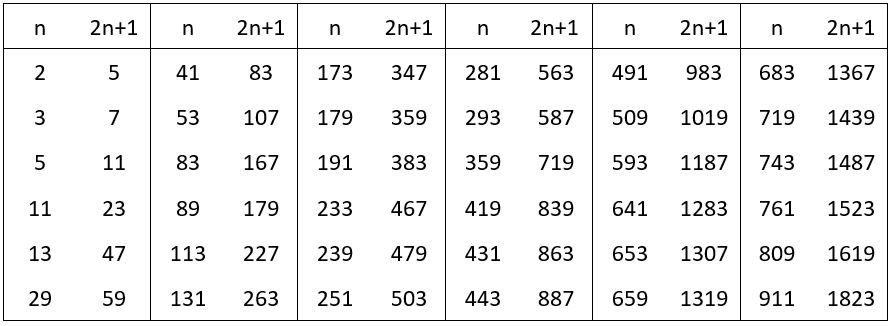
En excluant les six nombres de la première colonne de la série ci-dessus, tous les Nombres premiers de Sophie Germain sont de la forme :
11 + 30 n ; 23 + 30 n ou 29 + 30 n, où « n » est un entier.
Mais la réciproque n’est pas vraie : les nombres de la forme :
11 + 30 n ; 23 + 30 n ou 29 + 30 n, où n est un entier, ne sont pas tous des nombres premiers.
Une généralisation
On peut imaginer une infinité de séries numériques construites sur le modèle des Nombres de Queneau et/ou le modèle des Nombres de Sophie Germain.
Voici à titre d’exemple, la série des nombres « n » tels que « n2 + 1 » est un nombre premier, inférieurs à 100, pochés dans un « Crible d’Eratosthène » : on en compte 19, placés essentiellement dans les colonnes n° 4 et 6 ; parmi ces 19, seuls 1 et 2 sont premiers. On trouve cette série sous le n° A005574 de l’OEIS.
Une Méthode de construction des carrés latins : La Méthode de la Spirale.
On peut considérer la Méthode de la Spirale, comme une méthode de construction des carrés latins.
Cette méthode a pour point de départ, rappelons-le, la suite des n premiers nombres entiers placés dans la première ligne de la grille d’ordre n, de n2 cases.
Par exemple pour le carré latin d’ordre n = 6, issu de la Sextine, il s’agit de la suite « 1, 2, 3, 4, 5, 6 »
Or cette suite peut être présentée suivant l’une ou l’autre des nombreuses permutations de ces chiffres.
Le nombre de permutations, dans le cas ci-dessus, soit n ! = 6 ! = 720, correspond ainsi au nombre de solutions de carrés latins d’ordre n = 6, construits pas cette méthode, qui peut être considérée comme particulièrement prolifique, malgré ses limites d’application.
Rappelons en effet que la Méthode de la spirale n’est applicable que pour les ordres n correspondant aux Nombres de Queneau.
Matériellement sur le papier, l’application de la Méthode de la Spirale, n’est faisable que pour n relativement petit, n=9, ou bien, n=14, ce qui n’est déjà pas très aisé.
▶ The Poetry of Arnaut Daniel – Ed. J.J. Wilhelm – New York & Londres – Galand 1981
▶ Ataüt d’Arnaut Daniel – Tombeau d’Arnaut Daniel – Avant-propos de Jacques Roubaud – Letras d’Oc, Editeur 2017
▶ R. Lavaud – Les poésies d’Arnaut Daniel – Annales du Midi -1910, 22-86, pp. 162-179
▶ Anthologie de l’Oulipo – Ed. Marcel Benabou & Paul Fournel – Gallimard 2009.
▶ Sandrine Bedouret-Larraburu – N-nines encore ! De la Sextine d’Arnaut Daniel aux n-nines oulipiennes – APPA – ALTER 7
▶ Jacques Roubaud – N-nines, autrement dit Quenine (encore) – La Bibliothèque oulipienne, n° 66, p. 6.
▶ Jacques Roubaud – Un problème combinatoire posé par la poésie lyrique des troubadours – Mathématiques et Sciences humaines –27, 1969, pp. 5 – 12.
▶ Jacques Roubaud – Réflexions historiques et combinatoires sur la n-ine, autrement dit Quenine – La Bibliothèque oulipienne – 5 ( 66 ) 2000, pp. 99 – 124.
▶ Jacques Roubaud – N-ine, autrement dit Quenine ( encore ) La Bibliothèque oulipienne – n° 66 – p. 6
▶ U. A. Canello – La Vita e le Opere del Trovatore A. Daniello – Hale 1883.
▶ Jean-Guillaume Dumas – Caractérisation des quenines et leur représentation spirale , Mathématiques
et sciences humaines 84 | Hiver 2008, URL : http://journals.openedition.org/msh/10946
▶ Vanessa Vallet – Entre mathématiques et littérature : les nombres de Queneau. UFR de Mathématiques et d‘Informatique – 2008.
▶ Michèle Audin – Poésie, spirales et battements de cartes – Images des Mathématiques, du CNRS – 26 septembre 2009.