Les cercles magiques du carré de Dürer
On peut inscrire dans un cercle vingt huit configurations différentes des 4 termes (dont les 4 permutations figurées : 11*, 12*, 51*, 52*) donnant la constante magique dans le carré magique de Dürer. Ces formations sont matérialisées dans les grilles ci-après, extraites de la grande planche des 86 combinaisons de 4 termes, dont la somme est égale à la Constante Magique M4 = 34.
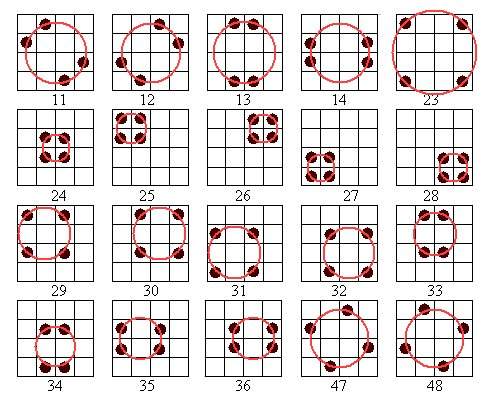
On remarque que certains cercles se superposent, ainsi dans les formations des grilles 11, 12, 13, 14, 47 et 48, ce qui réduit à 15 le nombres de cercles distincts
Le carré de Dürer en numération binaire
Dans cette manipulation, on considère le carré de Dürer réalisé avec la série des 16 entiers consécutifs de 0 à 15
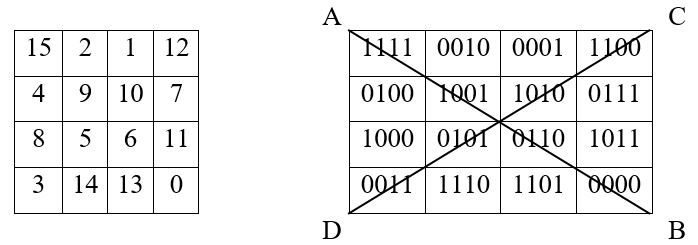
Rappelons la numération binaire correspondante :

On remarque alors, dans cette configuration :
– que les termes symétriques par rapport à la première diagonale A B sont symétriques l’un de l’autre ;
– que les termes symétriques par rapport à la seconde diagonale C D sont « miroir » inversé l’un de l’autre (les chiffres 1 et 0 sont intervertis)
On le voit mieux dans la présentation ci-dessous :
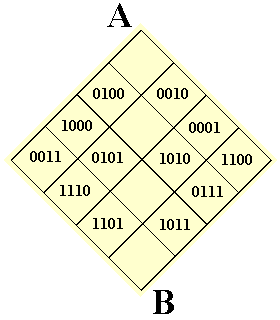
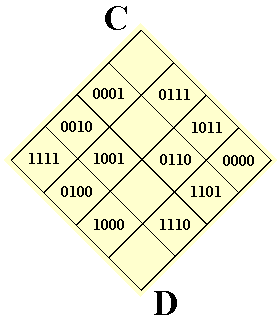
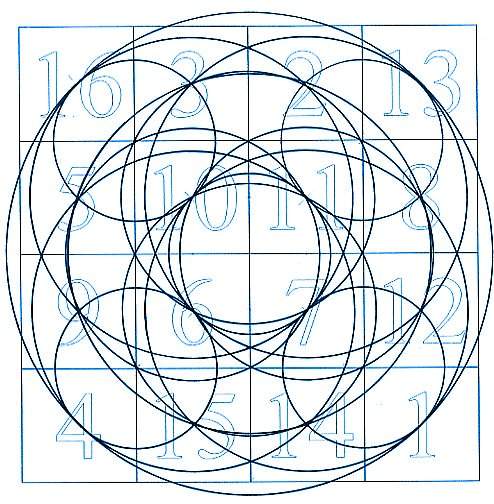
Le parcours graphique du Carré de Dürer.
Voici quelques connections faisant apparaître de mystérieux hexagones entrelacés…
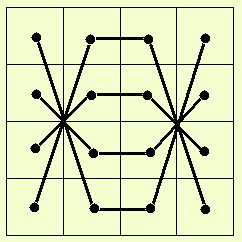
Dans cette grille , on a relié les séries 0, 1, 2, 3 ; 4, 5, 6, 7 ; 8, 9, 10, 11 ; 12, 13, 14, 15.
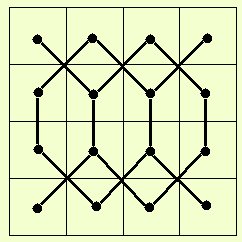
Dans la grille de droite, on a relié d’une certaine façon 3 séries de 4 nombres pairs entre eux
2, 4, 8, 14 ; 2, 10, 6, 14 ; 0, 6, 10, 12
et 3 séries de 4 nombres impairs entre eux
3, 5, 9, 15 ; 1, 9, 5, 13 ; 1, 7, 11, 13, de haut en bas.
Le carré magique de Dürer est du type « associé ».
Un carré magique est dit du type « associé », lorsque les termes complémentaires sont placés dans les cases complémentaires de la grille. Cela correspond au type de base III de la Classification de Dudeney.
Rappelons que dans une série, les termes dits « complémentaires » sont symétriques par rapport au milieu de la série.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
Ainsi 3 et 14, 6 et 11, 8 et 9….. sont des termes complémentaires dans la série ci-dessus ; par suite leur somme est constante et égale à la somme des termes extrêmes (cas d’une série paire).
Dans une grille de n x n = n2 cases, les cases symétriques par rapport au centre de la grille sont dites « complémentaires »
Dans un carré magique du type associé, la somme P des termes complémentaires placé dans les cases complémentaires est constante et égale à (n2 + 1) : c’est la « constante de polarisation ». Dans le carré magique de Dürer, de type associé, cette constante de polarisation est donc : P = n2 + 1 = 42 + 1 = 17
Les carrés magiques de type associé sont auto-complémentaires.
Rappelons que lorsque l’on remplace chaque terme d’un carré magique normal d’ordre n par son complémentaire à (n2 + 1), on obtient un autre carré magique de même constante linéaire, dit « complémentaire » du précédent.
Exemple pour le carré de Dürer :
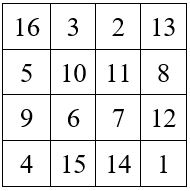
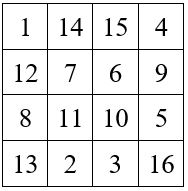
Si le « Complémentaire » coïncide après rotation avec le carré d’origine, ce dernier est alors dit « auto-complémentaire ». C’est bien le cas des carrés magiques du type associé, et en particulier du Carré de Dürer.
Remarque – Les carrés fondamentaux ou naturels répondent à la définition du type « associé », bien que n’étant pas des carrés magiques.
De type associé, le carré magique de Dürer est « semi-pandiagonal », c’est-à-dire que la constante magique est obtenue sur les seules diagonales brisées dont les termes présentent une symétrie centrale ( ou suivant une diagonale principale) . Ainsi on a : 5 + 3 + 14 + 12 = 34 et 9 + 15 + 8 + 2 = 34
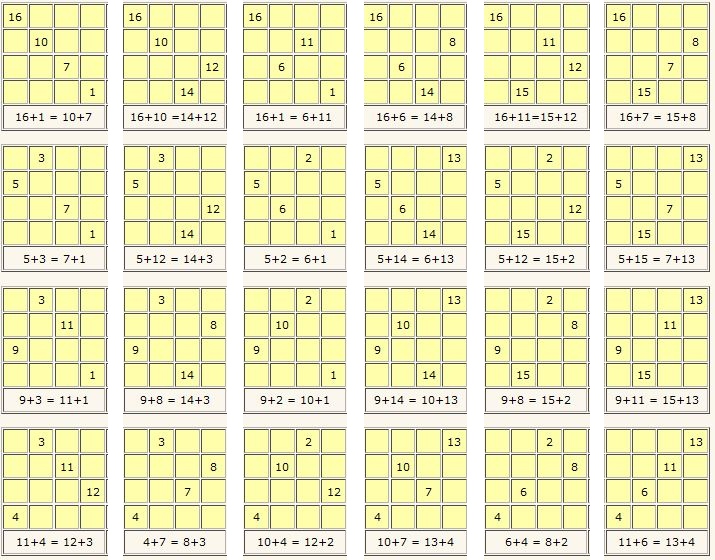
Des couples « isométriques » dans les permutations figurées.
Rappelons ci-dessous les 24 permutations figurées de 4 termes :
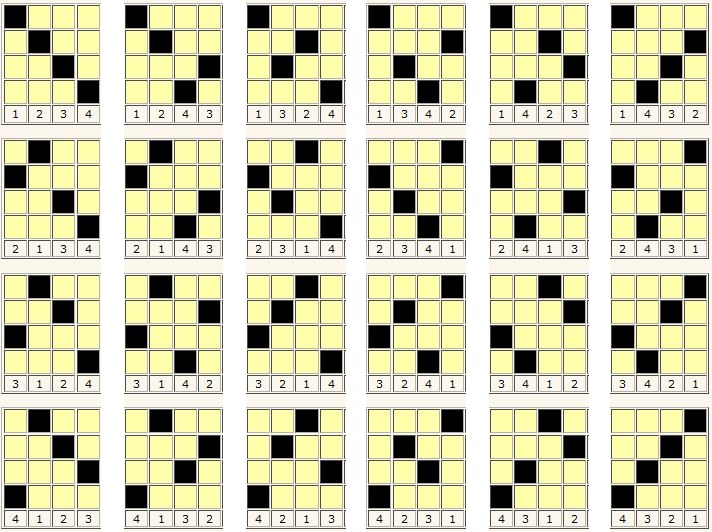
Dans le carré de Dürer, les 4 termes qui correspondent par superposition à une permutation figurée d’ordre 4, forment deux couples de trois façons. Or il y a toujours deux couples dont les sommes sont égales. Cette propriété est visualisée dans les 24 grilles ci-dessous, qui correspondent aux 24 permutations figurées d’ordre 4. Cette propriété remarquable est souvent occultée.