Ce blog est basé sur les ouvrages de René Descombes, il comprend quelques parties adaptées des livres et d’autres informations inédites que l’auteur n’a pas pu faire figurer dans les livres… Les sujets présentés couvrent les récréations mathématiques, les carrés magiques et naturels, l’histoire de la batellerie.
Certaines œuvres d’art, des curiosités et des jeux en lien avec ces domaines seront également présentées.
Les derniers articles du blog ….
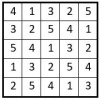
Les carrés magiques répétitifs – Partie 4
Construction d’un carré magique répétitif d’ordre n=6 Une méthode de construction prolifique Retrouvons une construction simple du carré magique ou semi-magique répétitif. Soit par exemple dans la grille d’ordre n = 6 de 36 cases. On choisit une permutation figurée ; précisons déjà que l’on a le choix entre : 6 ! = 720 permutations figurées possibles dans la… Lire la suite »Les carrés magiques répétitifs – Partie 4

Les carrés magiques répétitifs – Partie 3
Construction d’un carré magique répétitif d’ordre n=16 Un beau carré magique répétitif d’ordre n = 16 Une proposition de Hannes Bürgel Dans la demie-grille supérieure du carré magique potentiel, les 8 sous-carrés de 16 cases sont issus de 8 permutations des lignes du carré naturel alterné normal d’ordre n = 4, lequel figure dans le… Lire la suite »Les carrés magiques répétitifs – Partie 3

Les carrés magiques répétitifs – Partie 2
Construction d’un carré magique répétitif d’ordre n = 8 Le carré magique normal d’ordre n = 4 est le catalyseur Le carré magique normal d’ordre n = 4, choisi comme catalyseur, est un carré magique normal à quartiers égaux, de somme : S = 34 On place ce carré magique catalyseur dans une grille d’ordre n… Lire la suite »Les carrés magiques répétitifs – Partie 2

Les carrés magiques répétitifs – Partie 1
La magie primaire. Rappel. Le carré magique normal ou primaire classique utilise une seule fois la suite des n2 premiers entiers pour obtenir la magie des lignes, des colonnes et des deux diagonales centrales. Exemples pour n = 4 : Première méthode de construction. On sélectionne les termes de la couronne périphérique dans le carré naturel d’ordre… Lire la suite »Les carrés magiques répétitifs – Partie 1

Les carrés magiques répétitifs
Dans un carré magique normal d’ordre n, la suite des n2 premiers entiers est utilisée une seule fois. Lorsque l’on utilise plusieurs fois une suite des premiers entiers pour obtenir la magie dans les lignes, les colonnes et les deux diagonales centrales, on qualifie ce carré magique de carré magique répétitif normal. Cette catégorie de… Lire la suite »Les carrés magiques répétitifs
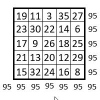
Construction des carrés magiques : La Méthode des progressions arithmétiques
Introduction La méthode de construction du carré magique normal proposée, a pour origine la propriété suivante du carré naturel : Dans tout carré naturel, les termes des colonnes (ou des lignes) sont en progression arithmétique de raison r=n, tandis que les termes des lignes (ou des colonnes) sont dans l’ordre naturel, r=1. On le vérifie aisément… Lire la suite »Construction des carrés magiques : La Méthode des progressions arithmétiques
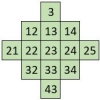
Où vont se cacher les permutations figurées dans le carré naturel ?
Propriétés des grilles carrées implantées dans le carré naturel. Soit par exemple le carré naturel d’ordre n = 10 de 100 cases. On observe rapidement que les termes situés sur les permutations figurées dans chaque grille carrée, ont même somme. Ainsi dans la fenêtre d’ordre n = 4 de 16 cases, encadrée ci-contre, on dénombre :… Lire la suite »Où vont se cacher les permutations figurées dans le carré naturel ?
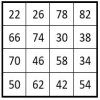
Progressions arithmétiques et carrés magiques
Certaines progressions arithmétiques génèrent des carrés magiques par addition, intéressants par leur composition, que nous nous proposons de présenter, de préciser et de développer. Le carré magique normal. Tout d’abord, on qualifie de normal le carré magique d’ordre n, dont les n2 termes sont les n2 premiers nombres entiers.Exemple ci-contre : La Lyre correspond au carré… Lire la suite »Progressions arithmétiques et carrés magiques
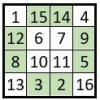
Construction des carrés magiques : La Méthode des nombres complémentaires sur les diagonales
Cette méthode inédite, permet de construire des carrés magiques en utilisant les nombres complémentaires sur les diagonales. Carrés d’ordre n=4 On part du carré naturel d’ordre n = 4 ( Grille 1 ), dans lequel on remplace les nombres situés sur les diagonales centrales par leur complément à : n2 + 1 = 17 ( Grille… Lire la suite »Construction des carrés magiques : La Méthode des nombres complémentaires sur les diagonales
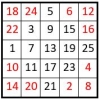
Construction des carrés magiques impairs : La méthode Conway
John Horton Conway ( 1937 – 2020 ) est un mathématicien britannique, bien connu en particulier, comme inventeur du Jeu de la Vie, entre autres. Dans la méthode de construction des carrés magiques normaux d’ordre impair, n=2 k + 1, mise au point par J. H. Conway, les nombres impairs et les nombres pairs sont… Lire la suite »Construction des carrés magiques impairs : La méthode Conway
Pour les articles plus anciens, merci de naviguer dans les différentes catégories !