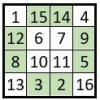
Cette méthode inédite, permet de construire des carrés magiques en utilisant les nombres complémentaires sur les diagonales.
Carrés d’ordre n=4
On part du carré naturel d’ordre n = 4 ( Grille 1 ), dans lequel on remplace les nombres situés sur les diagonales centrales par leur complément à : n2 + 1 = 17 ( Grille 2 ).
Cette opération revient à permuter les nombres à égale distance du centre sur ces diagonales, c’est-à-dire les nombres complémentaires.
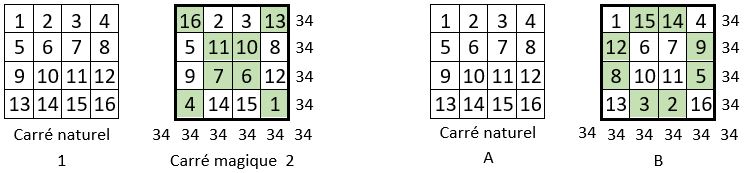
On ne touche pas aux autres nombres, qui sont à leur place définitive.
La Grille 2 est un carré magique normal, de Constante magique M4 = 34 ; c’est un carré magique de type associé, de Constante de polarisation M4 = n2 + 1 = 17.
C’est aussi un carré magique aux quartiers égaux, de somme M4 = 34.
Variante
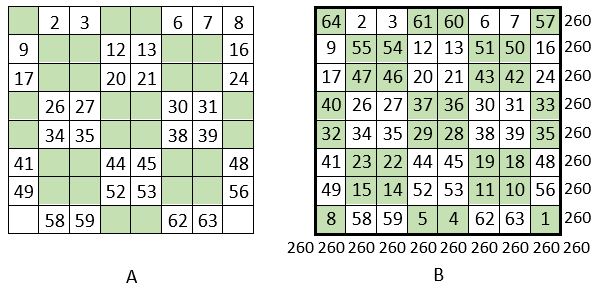
on peut tout aussi bien ne pas toucher aux nombres situés sur les diagonales centrales, et remplacer les autres nombres par leur complément à n2 + 1 = 17 ( Grilles A et B ci-dessus ) : on obtient le même carré magique, à une rotation près.
Cas particulier
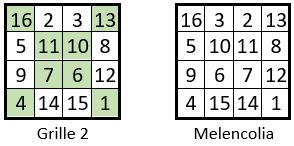
On obtient le carré magique de la Melencolia
d’Albrecht Dürer ( 1514 ), après permutation des colonnes centrales de la Grille 2
Carrés d’ordre n=8
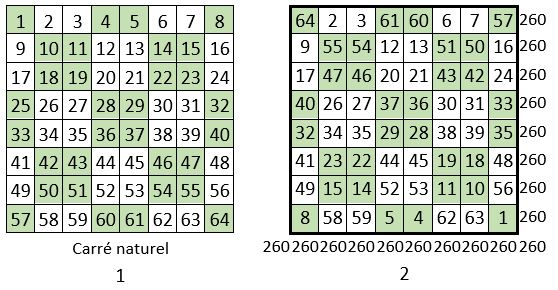
Dans les diagonales des quatre sous-carrés d’ordre n = 4 ( Grille 1 ), on remplace les nombres qui s’y trouvent, par leur complément à : n2 + 1 = 82 + 1 = 65 ( Grille 2 )
Ce qui revient à faire les permutations des nombres complémentaires du carré naturel d’ordre n = 8, qui sont situés sur les diagonales centrales des quatre sous-carrés d’ordre n = 4.
On obtient un carré magique normal, d’ordre n = 8, de Constante magique M8 = 260 ; c’est un carré magique de type associé, de Constante de polarisation P8 = n2 + 1 = 65 ; et c‘est un carré magique à quartiers égaux, de somme M8 = 260.
Remarque.
Voici une autre présentation pour la construction de ce carré magique :
On compte mentalement les nombres de la série des n2 premiers entiers, en commençant par la première case de la première ligne, en descendant, et l’on inscrit les nombres qui ne correspondent pas aux diagonales centrales des quatre sous- carrés d’ordre n = 4 ( c’est-à-dire les cases non pochées de la Grille A ci-dessus )
On fait alors le même comptage, en commençant par la dernière case de la dernière ligne, en remontant, et l’on inscrit les nombres qui correspondent aux diagonales centrales des sous-carrés d’ordre n = 4 ( c’est-à-dire les cases pochées de la Grille B ci-dessus )
On obtient le même carré magique que celui obtenu par la méthode qui précède.
Il s’agit d’une application de la Méthode des pointages, qui est relativement plus simple, ne nécessitant aucun calcul.