Claude Gaspard Bachet de Méziriac (1581-1638), dans ses » Problèmes plaisants et délectables qui se font par les nombres » (1612), restés célèbres, donne une méthode simple pour la construction des carrés magiques d’ordre impair. Cette méthode est très connue.

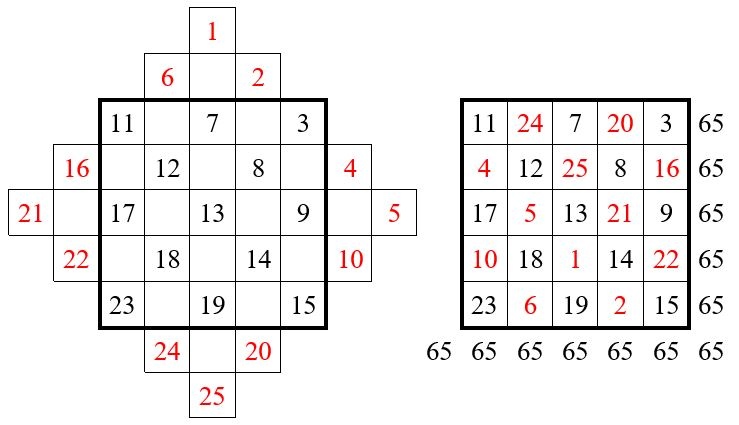
Soit l’exemple d’un carré magique d’ordre n = 5. On écrit les n2 = 25 premiers entiers dans la grille crénelée ci-dessus, dans les cases en diagonales à 45°.
Et l’on transfert les éléments qui se trouvent hors de la grille centrale carrés de 5 x 5, à leur antipode. On obtient le carré magique ci-dessus, de constante magique M5 = 65.
Il y a huit façons de placer les n2 premiers entiers dans la grille crénelée correspondant à l’ordre n. On obtient huit formes du carré magique, qui se déduisent toutes les unes des autres par rotation ou symétrie.
Bien sûr cette méthode s’applique au carré d’ordre n = 3 : les 8 façons de placer les chiffres de 1 à 9 dans la grille crénelée, donnent les 8 formes du Lo Shu.
On peut systématiser la Méthode de Bachet de Méziriac, par exemple pour n = 5, raison r, et premier terme a.
On constate que dans toutes les lignes, les colonnes et les deux diagonales principales, la somme linéaire ou constante magique de ce carré est : M’5 = 5a + 60 r
Ce qui constitue une démonstration particulière de la méthode de Bachet de Méziriac.
Plus généralement, la constante magique est donnée par le relation :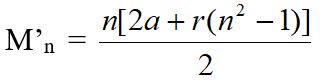
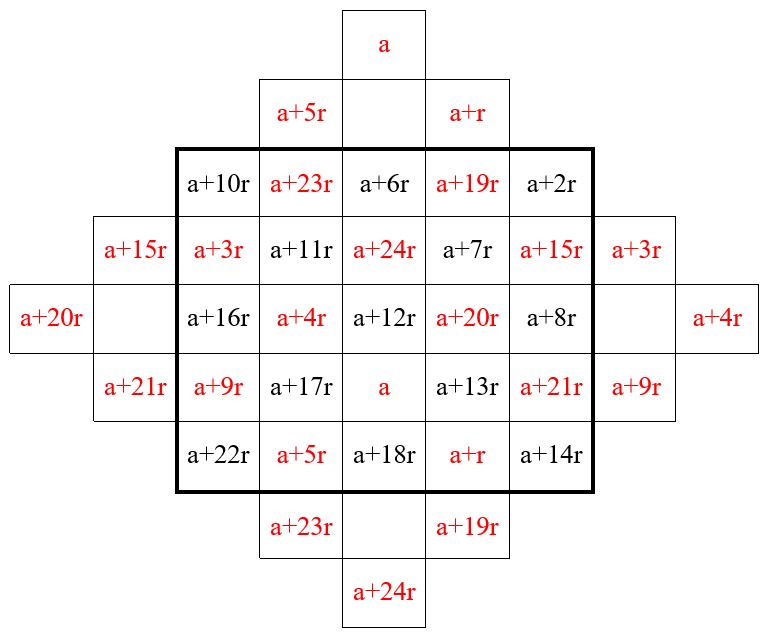
Une autre présentation de la Méthode de Bachet de Méziriac
Dans la grille précédente, on constate aisément dans la suite des entiers consécutifs à partir de l’unité, un cheminement régulier : un pas vers le bas, un pas à droite (1,1). Lorsque l’on aboutit à une case déjà occupée, on saute une case vers le bas (2,0): 1, 2, 3, 4, 5 et 6. Le point de départ est situé au-dessous de la case centrale : Application pour n = 7. Constante magique M7 = 175. (Grille ci-contre à droite)
On peut appliquer cette méthode avec un point de départ quelconque : on obtient alors un carré semi-magique. Le point de départ fixé au-dessous de la case centrale conduit toujours à un carré magique.
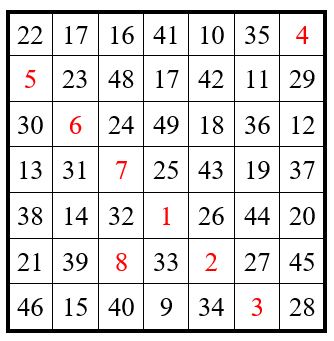
La Méthode de Labosne-Méziriac
En s’inspirant de Bachet de Méziriac, le Professeur Labosne, dans la nouvelle édition des » Problèmes plaisants… « , présente une méthode pour construire des carrés magiques ou semi-magiques, en progression non régulière d’ordre impair. Soit l’exemple ci-dessous d’un carré d’ordre n = 7.
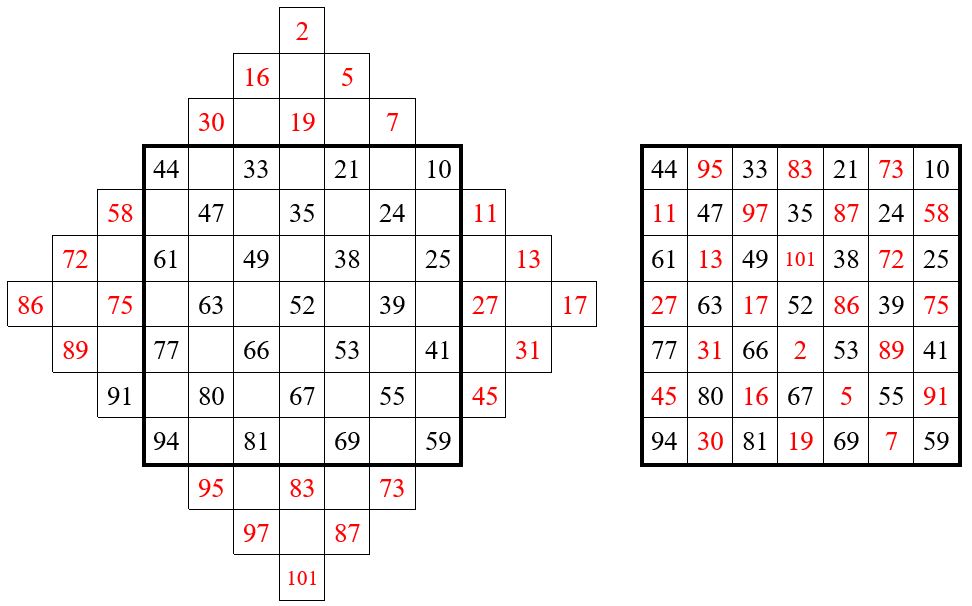
On inscrit n nombres quelconques, les » nombres de base « , dans un ordre quelconque, dans les n cases à 45° de la grille crénelée, par exemple la série 2, 5, 7, 10, 11, 13, 17.
On complète les alignements perpendiculaires correspondants, par les termes d’une progression arithmétique de raison r = kn , soit ici, avec k = 2, r = 2 n = 2 x 7 = 14. On effectue les translations de la méthode de Bachet de Méziriac.
La constante magique des lignes et des colonnes est obtenue dans cet exemple sur une seule diagonale : M’7 = 359. On a donc affaire à un carré semi-magique.
Le nombre de permutations de la série des n » nombres de base « , est n ! = 7 ! = 5.040, qui donne autant de solutions différentes, sans compter les 8 façons de placer la série choisie des » nombres de base » dans la grille crénelée.
Comme le choix des » nombres de base » est illimité, cette méthode peut don être considérée comme très prolifique, donnant des carrés magiques ou semi-magiques.
Pour n = 5, on essaiera par exemple la série : 2, 5, 7, 10 11 (c’est l’exemple donné par Labosne); on obtient bien un carré magique, de constante magique M’5 = 135 ( pour n = 5, on a 5 ! = 120)
Nota. La méthode de Labosne-Méziriac est à l’origine d’une méthode de construction des carrés magiques d’ordre impair, en progression non régulière, n termes arbitraires étant placés dans la grille suivant un positionnement spécifique.
