Philippe de La Hire (1640-1718) fut poussé vers la peinture par son père Laurent de La Hire, qu’il étudie à Rome. A partir de 1664,de retour à Paris, Philippe de La Hire se tourna vers les sciences et montra des intérêts très diversifiés : cartographe du royaume, il s’intéressa à la géométrie, à l’hydraulique, à la gnomonique, à la mécanique ainsi qu’à l’astronomie.
Il traduit le mémoire de Manuel Moschopoulos relatif aux carrés magiques, ce qui le conduit à travailler lui-même sur le sujet.

La méthode de construction des carrés magiques (d’ordre impair) décrite ci-dessous a pour origine les travaux de Philippe de La Hire publiés en 1705 par l’académie royale des sciences : Nouvelles constructions et considérations sur les carrés magiques, avec démonstrations.
Soit le cas de n = 7. M7 = 175
On construit deux carrés latins auxiliaires I et II de la manière suivante :

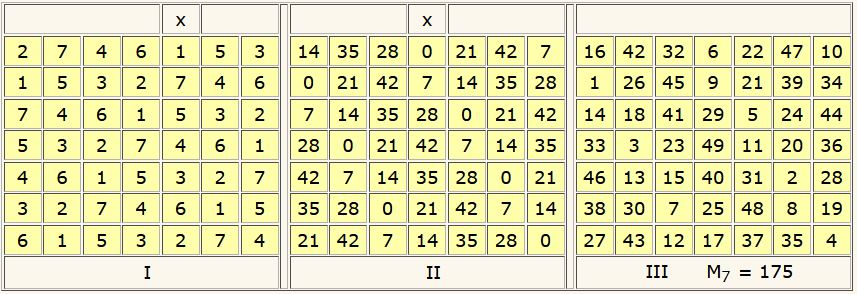
I – On écrit la suite des entiers de 1 à n dans un ordre quelconque dans la première ligne. Dans la seconde ligne on écrit ces mêmes nombres entiers dans le même ordre, en commençant par le nombre de la case qui suit immédiatement la case centrale de la ligne précédente (x) ; et ainsi de suite.
II – On écrit les nombres de la série [ 0, n, 2n, 3n, …] dans un ordre quelconque dans la première ligne ; dans notre exemple, pour n =7 , cette série est : [ 0, 7, 14, 21, 28, 35, 42] ; dans la seconde ligne on écrit ces mêmes nombres dans le même ordre, en commençant par le nombre qui se trouve dans la case centrale de la ligne précédente (x) ; et ainsi de suite.
III – On additionne les cases homologues de ces deux carrés latins auxiliaires, pour former le carré magique III, de constante magique M7 = 175.
Progéniture de la Méthode de De La Hire
Il y a n ! permutations possibles des éléments de chacune des premières lignes des deux carrés latins auxiliaires I et II. On peut donc former N = n ! x n ! couples de ces deux carrés latins auxiliaires, et autant de carrés magiques III, résultant de l’addition de ces couples.
Pour n = 5, on aura : 5 ! x 5 ! = 120 x 120 = 14.400
Pour n = 7, on aura : 7 ! x 7 ! = 5.040 x 5.040 = 25.401.600.
Quelques dessins techniques de Philippe de La Hire