
Ralph Strachey (1868-1923) fut ingénieur civil en Inde.
La Méthode de Ralph Strachey s’applique :
- aux carré d’ordre n = 2(2k+1), ou » impairement pairs « , c’est-à-dire à n = 6, 10, 14, 18, 22…
- aux carrés d’ordre n = 4k ou » pairement pairs « , c’est-à-dire à n = 4, 8, 12, 16…
Carrés d’ordre n = 2(2k+1) : n divisible par 2,mais pas par 4.
Prenons l’exemple n = 10 ; k=2.
On subdivise la grille de n2 cases en quatre sous-carrés : A, B, C, D.
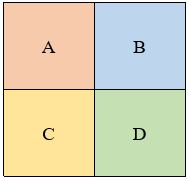
On remplit successivement les sous-carrés A, C, B et D de la manière suivante:
Il faut qu’il y ait 2 fois le chiffre 3 par ligne.
La diagonale » haut-gauche-bas-droit » doit compter 3 fois le chiffre 3.
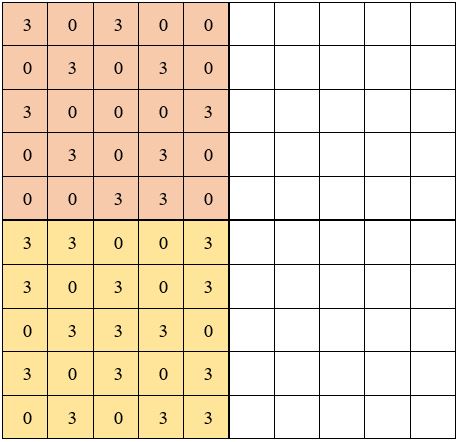
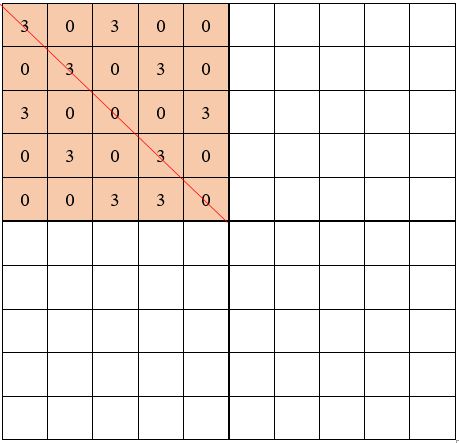
On considère les cases symétriques par rapport au côté commun aux sous-carrés A et C.
Et l’on permute, dans les cases correspondantes du carré C, les chiffres 0 et 3.
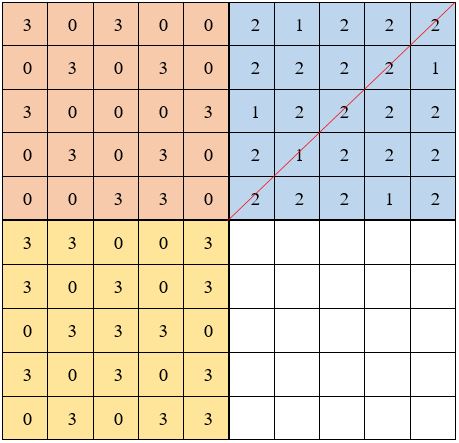
Il faut qu’il y ait 4 fois le chiffre 2 par ligne.
La diagonale » haut-droit/bas-gauche » doit compter 4 fois le chiffre 2.
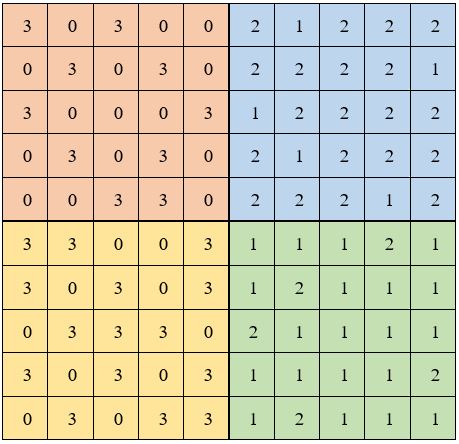
Toutes les cases des quatre sous-carrés de la grille initiale sont remplies.
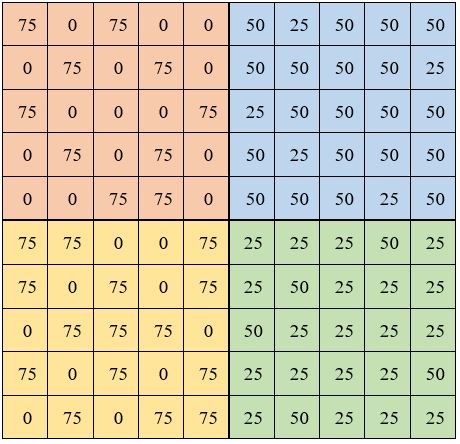
On multiplie alors tous les chiffres de ces cases par le facteur n2/4 = 102 /4 = 25. On obtient le carré auxiliaire ci-contre:
Mais ce n’est pas encore le carré magique normal que l’on veut construire.
Pour le ramener à la normale, il faut additionner à chaque sous-carré, un carré magique d’ordre 5, ainsi qu’il suit :
- pour les sous-carrés A et B, on ajoute ce carré magique;
- pour les sous-carrés C et D, on ajoute son symétrique par rapport à l’horizontale.
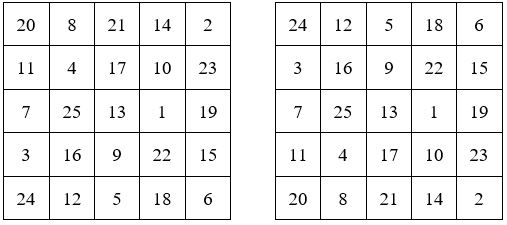
Pour A et B
Pour C et D
Ainsi par exemple, soit le carré magique d’ordre 5 ci-dessus, et son symétrique au-dessous ( on a le choix, rappelons qu’il y a 275.305.224 carrés magiques d’ordre 5 !)
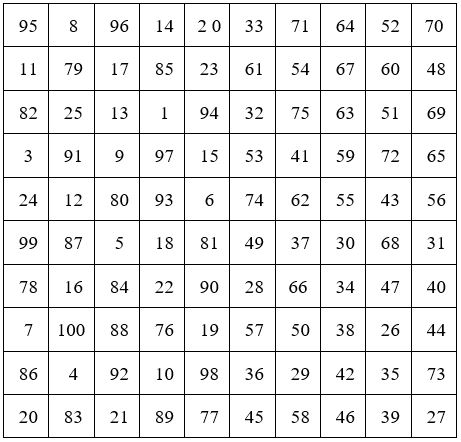
Il ne reste plus qu’à superposer à leurs places respectives les carrés d’ordre 5 indiqués ci-dessus, dans le carré auxiliaire précédent, et faire la somme case par case. On obtient le carré magique d’ordre 10 ci-après, de constante magique M10 = 505.
Cette méthode, un peu lente et pas très simple, est très riche. Comme il y a de multiples façons de remplir les sous-carrés A et C, cela multiplie d’autant le choix du carré magique d’ordre 5.
La famille des carrés magiques d’ordre n =10 est vraiment impressionnante (Voir ci-après: La progéniture de Ralph Strachey).
Carrés d’ordre n = 4k ( » pairement pair « )
Soit l’exemple n = 8 ; k = 2.
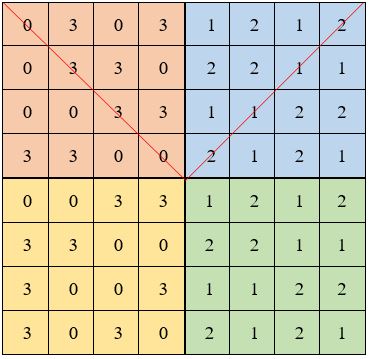
La seule différence par rapport à la technique précédente, réside dans le remplissage des sous-carrés A et C:
Chaque ligne doit comporter le même nombre de chacun des couples de chiffres 0 et 3; 1 et 2.
Les règles sont les mêmes pour les diagonales.
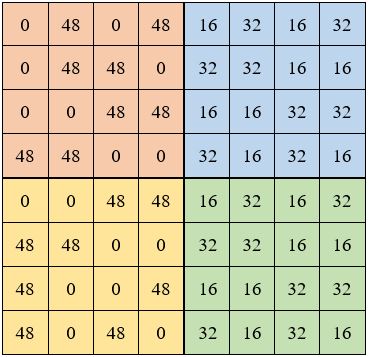
Les autres étapes sont identiques à celles de la méthode précédente.
Rappelons qu’il y a le choix pour le carré d’ordre 4, entre les 880 carrés de cette famille.
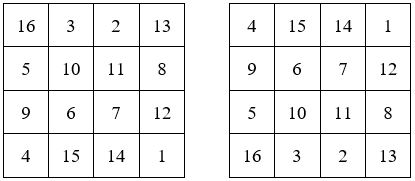
Carré de Dürer
pour A et B
Et son symétrique
pour C et D
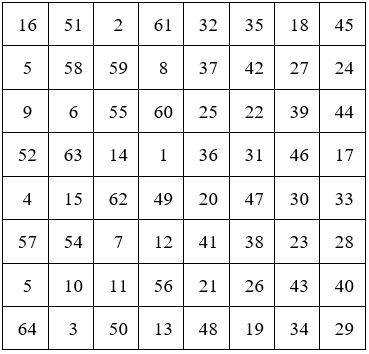
La progéniture de Ralph Strachey
- Carrés d’ordre » pairement pair » : n = 8
Lors du remplissage du sous-carré A, il y a 6 façons de placer » 0,3,0,3 » sur 4 cases. Pour l’ensemble des 4 lignes, on aurait donc 64=1296 dispositions différentes. La contrainte d’avoir 2 fois le chiffre 3 sur une diagonale, ramène ce nombre à 486. Il en est de même pour le sous-carré B. Et comme on a le choix entre les 880 carrés d’ordre 4, le nombre de carrés magiques d’ordre 8 que l’on peut construire par cette méthode sera 486 x 486 x 880 = 207.852.480. Ce nombre de plus de 200 millions, montre la richesse de la Méthode de Raph Strachey.
- Carrés d’ordre » impairement pair » : n = 10
Pour le sous carré A, il y a 10 façons de remplir les 5 cases avec les chiffres 0 et 3, soit pour 5 lignes, 105 = 100.000. La contrainte intéressant la première diagonale, ramène ce nombre à 15.360. Pour le sous-carré B, il y a 5 façons de remplir les 5 cases avec lec chiffres 1 et 2, soit pour les 5 lignes, 55 = 3.125, nombre qui est ramené à 1.280 pour tenir de la contrainte intéressant la seconde diagonale. Si l’on se souvient qu’il y a 275.305.224 carrés magiques d’ordre 5, le nombre de carrés magiques d’ordre 10 que l’on pourra construire avec la Méthode de Ralph Strachey s’établit à: 15.360 x 1.280 x 275.305.224 = 19.660.800 x 275.305.224 = 5,4 x 1015 soit plus de 5 millions de milliards ! (D’après Lucien Gérardin (1986), pp. 89-95 et 202-203)
