Cette méthode inédite est basée sur la propriété suivante du carré magique normal d’ordre impair :
Dans le carré magique normal d’ordre impair, n = 2 k + 1, les termes de chaque sous-série naturelle, sont situés sur une permutation figurée.
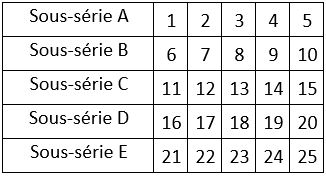
Prenons l’exemple de n=5. Les sous-séries naturelles se présentent ainsi dans le tableau ci-contre, sous la forme du carré naturel ou de la Lyre classique.
Voici ci-dessous l’implantation de ces sous-séries dans les permutations figurées d’un carré magique d’ordre n = 5 de type associé, de constante magique M5=65 et de constante de polarisation P5 = 26.
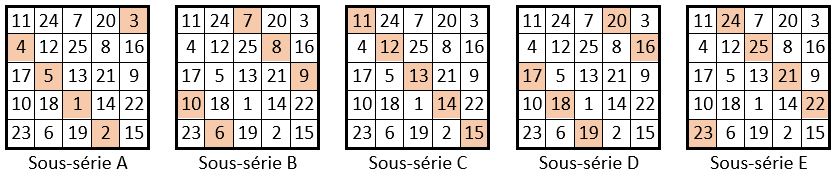
Il arrive cependant que cette propriété ne soit pas observée dans certains carrés magiques d’ordre impair, sans que l’on sache pourquoi.
La construction du carré magique d’ordre impair. Application n = 5.
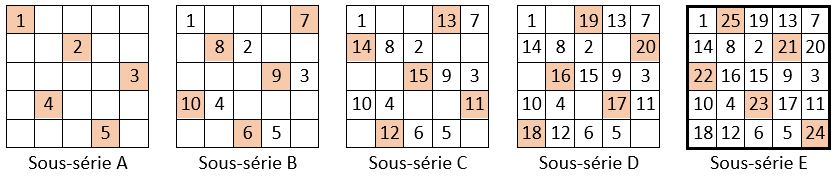
L’une des huit marches du cavalier des échecs, prise pour exemple, permet de placer les termes de la première Sous-série A sur une permutation figurée :
Marche principale : deux pas vers la droite ; un pas vers le bas.
Marche secondaire : un pas vers la gauche.
Cette implantation s’applique quel que soit le choix de la case-départ, la marche du cavalier choisie restant la même pendant tout le développement de la méthode.
Les placements successifs des séries suivantes s’effectuent en appliquant la même marche du cavalier, la case-départ du placement considéré étant située dans la case immédiatement à gauche du dernier terme de la Sous-série qui précède.
On obtient dans la Sous-série E, un carré magique normal d’ordre n = 5, de Cte magique M5 = 65.
C’est un carré magique pandiagonal, les diagonales centrales et brisées sont magiques. Les termes de chaque Sous-série, ainsi que ceux des diagonales centrales et brisées se superposent à une permutation figurée.
Cette méthode s’applique aux ordres impairs, quel que soit l’ordre dans lequel sont placées les lignes ou les colonnes du Tableau I, dont on peut permuter les lignes ou les colonnes.
Le Tableau II ci-dessous, présente différentes permutations ou échanges des lignes et des colonnes du Tableau I
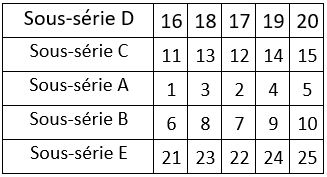
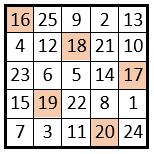
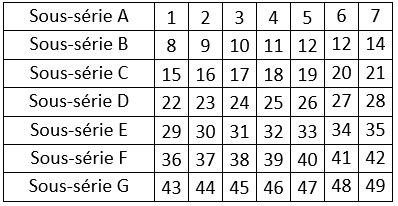
Dans cette application de la Méthode des permutations figurées, d’après le Tableau II ci-dessus des Sous-séries naturelles elles-mêmes permutées, on a adopté la même marche du cavalier que dans l’application qui précède, ainsi que la même case-départ. Le carré magique obtenu présente les mêmes propriétés que le carré magique obtenu avec la première application de la méthode.
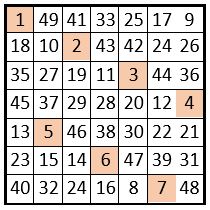
Voici une application de cette Méthode, pour un carré magique d’ordre n = 7, avec les sept Sous-séries naturelles dans leur état d’origine, non perturbées.
Mêmes marches principale et secondaire du cavalier, mêmes cases-départs que dans les applications qui précèdent. On obtient un carré magique pandiagonal; les termes des Sous-séries naturelles sont bien sur des permutations figurées.
Dénombrement (n = 5 )
Compte-tenu des huit marches du cavalier, de quatre marches secondaires, de n2 = 25 cases-départs d’une part, et des permutations possibles des lignes et des colonnes, soit chaque fois 5 ! = 120, d’autre part, on aurait au total : N5 = 8 x 4 x 25 x 120 x 120 = 12 580 000 solutions.
La formule générale donnant Nn = f ( n ) serait alors : Nn = 32 n2 ( n !)2
La Méthode des permutations figurées peut être considérée comme très prolifique.
