Manuel Moschopoulos, un moine grec qui vivait vers 1392 en Crète, est l’auteur d’un très ancien traité des carrés magiques : on peut le dater du début du XVe siècle. Son manuscrit fut traduit en latin par Philippe de la Hire (1640-1718), mathématicien et astronome français, qui le communiqua à l’Académie des Sciences en 1691; mais cette traduction ne nous est pas parvenue.
Le Traité de Moschopoulos a été traduit en français par Paul Tannery sur le texte grec en 1920.

Méthode des pointages ou des transpositions (n = 4)
Cette méthode est décrite avec des exemples de grilles d’ordre n = 4, 8 et 16. Cette méthode est donc très ancienne.
Elle s’applique aux ordres de la forme n = 4 k.
On commence par » pointer » la grille intéressée : il faut que dans chaque ligne et chaque colonne, la moitié des cases soient pointées, et par conséquent que l’autre moitié des cases ne soient pas pointées.
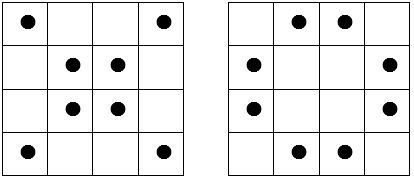
Pointage de type I
Pointage de type II
Ce pointage fait, avec l’un ou l’autre type de pointage, on remplit la grille en superposant de deux façons différentes la suite des entiers de 1 à n2=16.
On compte mentalement en commençant par la case en haut à droite, et on inscrit le nombre correspondant de la suite des entiers dans chaque case pointée.
Exemple ci-dessous avec le type de pointage I :
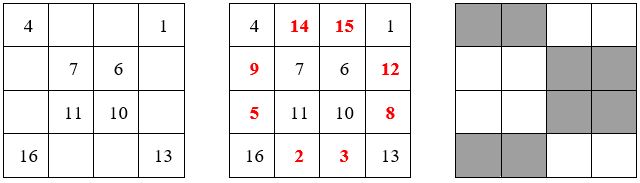
On remplit ensuite les cases vides, en comptant mentalement la même suite d’entiers, en commençant par la case diagonalement opposée à la case du départ de la première suite, c’est-à-dire en bas à gauche, dans notre cas, et on inscrit les nombres correspondants dans les cases non pointées au fur et à mesure qu’on les rencontre.
Exemple ci-dessus : c’est le Carré de Dürer.
On peut faire débuter le comptage de la suite des entiers dans un angle quelconque du carré; le second comptage débutera alors dans l’angle diagonalement opposé.
Cette méthode conduit également à un carré panmagique à quartiers égaux.
Méthode des pointages ou des transpositions (n multiple de 4 – n = 4k)
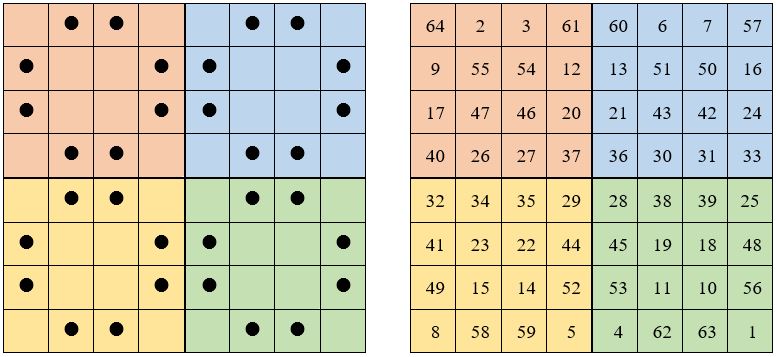
On divise la grille de côté n = 4k, en k2 carrés élémentaires de 4 x 4 = 16 cases, affectés du type de pointage choisi.
Et on » compte » de la même façon que précédemment pour remplir la grille.
Exemple pour n = 8 – k = 2, et k2 = 4 : on obtient un carré panmagique à quartiers égaux ; M8 =260 ; S = 520.
Méthode, dite « par 2 et 3 »
La première Méthode exposée par Moschopoulos pour les carrés d’ordre impair, a toujours pour point de départ la case située immédiatement au-dessous de la case centrale.
Les déplacements sont ainsi caractérisés :
Marche principale ( 1, 1 )
Marche secondaire ( 2, 0 )
Cette Méthode est dite « par 2 et 3 », car dans l’esprit de Moschopoulos ces deux chiffres rappellent la première étape – ou le premier pas – de chacun des déplacements : c’est le nombre de cases comptées, y compris la case départ, soit deux pour la marche principale, et trois pour la marche secondaire. Cela correspond ici à la Méthode de Bachet de Méziriac.
Voici deux exemples, un carré d’ordre 5 et un carré d’ordre 7, pris dans le Traité de Moschopoulos :
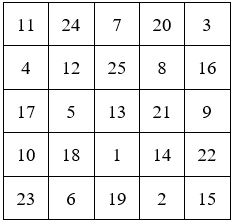
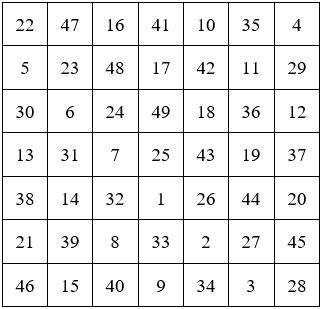
Le point de départ situé au-dessus de la case centrale donne un carré magique symétrique des précédents par rapport au centre de la grille.
Exemple pour le carré d’ordre 7.
On peut observer que la Marche Principale peut s’effectuer de 4 manières différentes : (1,1); (-1,1); (-1,-1); (1,-1)
Le point de départ situé dans la case contiguë à la case centrale, dans la direction du premier pas de la Marche Principale, donne un carré diagonal.
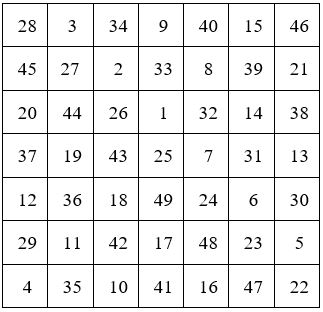
Pour un ordre impair donné, cette Méthode de Moschopoulos permet de construire :
– 4 carrés magiques (diagonaux), ou bien 8 au total si l’on compte les symétriques.
– 4 n2 carrés semi-magiques.
Méthode, dite « par 3 et 5 »
Le point de départ, dans cette seconde méthode présentée par Moschopoulos, est toujours situé dans la case du milieu de la première ligne du carré impair.
Les déplacements sont alors ainsi caractérisés :
Marche principale : ( 2, 1 )
Marche secondaire 🙁 4, 0 )
D’où la désignation, Méthode « par 3 et 5 » conformément à la convention retenue précédemment par Moschopoulos.
Voici deux exemples tirés du Traité de Moschopoulos :
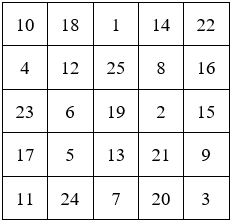
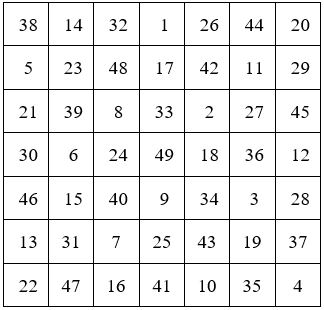
On peut remarquer dans ces exemples, que la seconde ligne de ces carrés magiques est identique dans les Méthodes (par 2 et 3) et (par 3 et 5) de Moschopoulos.
Cependant, la Méthode de Moschopoulos (par 3 et 5), donne des carrés panmagiques ou diaboliques, et ceci pour un point de départ quelconque. Moschopoulos en avait-il conscience ? En tous cas il ne le dit pas.
