On se propose de rechercher comment on peut construire un carré magique, en nombres discontinus, lorsqu’on se donne a priori son ordre n et sa constante magique M’n.
Sommaire
Les nombres de base sont placés dans la première ligne
Cas de n=3
Soit M’3 = 198 = a + b + c = 54 + 52 + 92 = 198
Dans un carré magique d’ordre n = 3, on sait que la case centrale vaut le 1/3 de la constante magique.
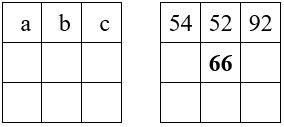
Dans un carré magique d’ordre n = 3, on sait que la case centrale vaut le 1/3 de la constante magique.
La valeur de la case centrale est donc : M’3 / 3 = 198 / 3 = 66
Il est alors facile de compléter les diagonales, dont on connaît deux termes sur trois, puis ensuite les trois colonnes, connaissant la somme linéaire M’3 = 198.
avec Trois séries homogènes de 3 termes ; r =12
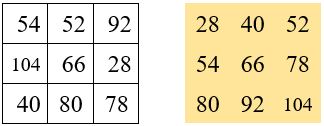
Les nombres de base a, b, c placés dans la première ligne conditionnent entièrement le carré magique ; on peut ainsi schématiser les opérations dans le tableau ci-contre :
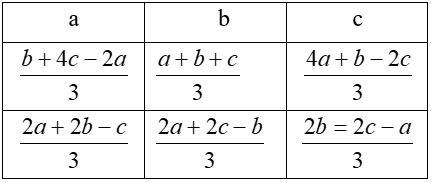
Conditions de magie.
◆ La constante linéaire choisie doit être divisible par 3, donc de la forme M’3 = a+b+c = 3 k.
◆ Les nombres de base ne doivent pas faire apparaître de répétition, ni au départ, ni au cours des opérations.
◆ Si on raisonne en nombres entiers positifs, les différentes opérations ne doivent pas faire apparaître de nombres négatifs ou fractionnaires.
A cet effet, posons pour simplifier: r= (a+b+c) / 3
Le tableau précédent se présente alors ainsi :

◆ Tous les nombres seront > 0 si l’on a : r > | a – c | et a, b, c > 2 r
◆ Enfin il y a tout intérêt à choisir les nombres de base dans une palette assez proches les uns des autres.
Remarque : cas où M’n n’est pas divisible par 3 .
M’n est de la forme M’n = 3 k + w, avec w = 1 ou 2
On peut opérer en deux étapes, de la manière suivante :
On construit d’abord le carré magique correspondant à M’3 = 3k
On ajoute ensuite w (soit 1 ou 2) aux trois termes d’une diagonale.
On obtiendra un carré semi-magique, avec une seule diagonale magique, de constante linéaire M’3 = 3 k + w.
Cas de n = 4
Soit M’4 = 220, que l’on peut décomposer arbitrairement ainsi : M’4 = 220 = 44 + 83 + 33 + 60
Soit s= M’4 / 2 = 220 / 2 = 110. Ainsi M’4 doit être divisible par 2, et donc de la forme M’4=2 k.
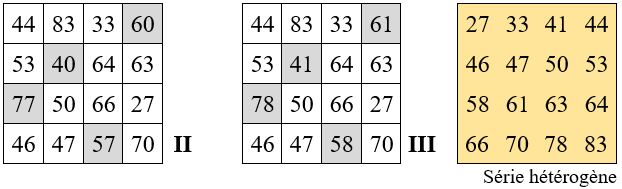
On place les compléments à s des nombres de base de la première ligne, conformément à la marche du fou aux échecs, c’est-à-dire en diagonale dans la troisième ligne (grille I).
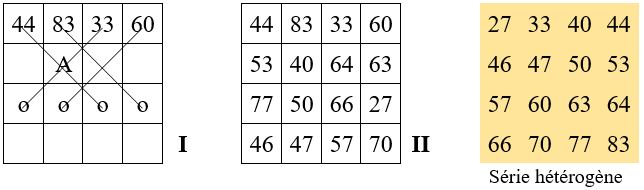
On choisit alors un nombre complémentaire A, (dans notre exemple A = 40), qui permet d’achever le remplissage de la grille II conformément aux opérations du tableau ci-dessous.
Rappelons que dans un carré magique d’ordre n = 4, la somme des quatre termes angulaires, ainsi que la somme des quatre termes en carré au centre, sont égales à la constante magique, soit M’4 = 2 s.
Notons que le nombre complémentaire A peut être placé n’importe où dans une case libre ; le tableau des opérations devra être modifié en conséquence.

Cas de M’4 impair, soit M’4 de la forme M’4 = 2 k + 1
Soit par exemple M’4 = 221 = 220 + 1. On résout le problème en deux temps :
- On construit d’abord un carré magique de constante M’4 = 220 : c’est le carré auxiliaire II ci-dessous (même exemple que ci-dessus).
- Ensuite on ajoute une unité aux nombres qui se trouvent placés sur une permutation figurée diagonale de 4 éléments : c’est le carré magique III ci-dessous, de constante magique M’4 = 221:
On pourrait donc construire théoriquement huit solutions, correspondant aux huit permutations figurées diagonales du carré magique d’ordre n = 4. Voici ces huit solutions :
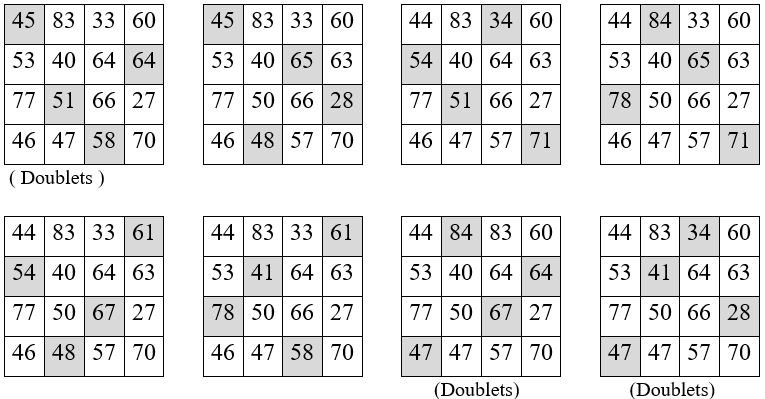
Attention ! : Certaines solutions comportant des doublets sont à éliminer ! Seules 5 solutions sont finalement acceptables, dans le cas de notre exemple.
Cas de n = 5
Ce cas de figure conduit à un carré magique à enceinte.
On décompose la constante Magique M’5, de la forme M’5 = 5 k, en une somme de 5 « nombres de base ».
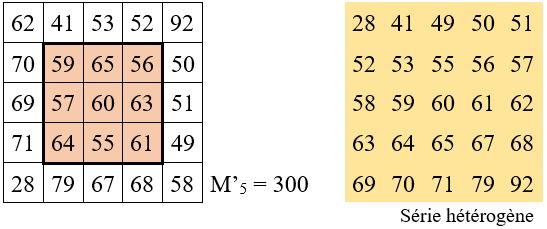
Soit M’5 = 300 = a + b + c + d + e = 62 + 41 + 53 + 52 + 92
On construit d’abord les bordures, après avoir placé dans la case centrale l’élément
r = (a+b+c+d+e) / n = 300 / 5 = 60
Deux nombres auxiliaires A et B sont nécessaires pour effectuer les opérations indiquées dans le tableau ci-dessous :
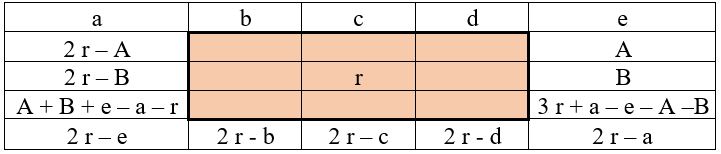
Application numérique : avec A = 50 et B = 51 ; r = 60.
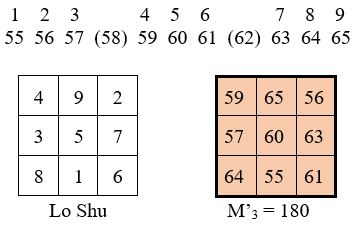
Quant au carré central d’ordre n = 3, on connaît sa case centrale ( 60), et donc sa constante magique
M’3 = 3 x 60 = 180.
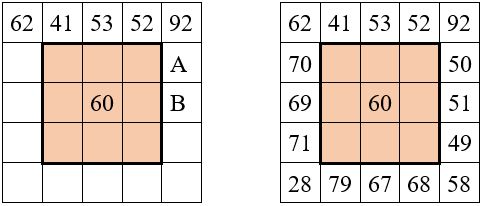
On prend modèle sur l’une des 8 formes du Lo Shu, en écrivant une suite de neuf nombres en progression arithmétique (r = 1), ayant au centre la case centrale 60, dans laquelle on élimine les nombres déjà employés dans les bordures :
Cas de M’5 non divisible par 5.
Lorsque M’5 n’est pas un multiple de 5, cette constante magique est de la forme :
M’5 = 5 k + w, avec w = 1, 2, 3 ou 4.
Soit par exemple : M’5 = 302 = 300 + 2 = ( 5 x 60 ) + 2
On résout alors le problème en deux étapes :
- Construction du carré magique auxiliaire de constante linéaire M’5 = 300
- On ajoute w = 2 aux termes occupant les cases d’une permutation figurée diagonale de 5 éléments.
On sait qu’il y a 20 permutations figurées diagonales de 5 éléments, ce qui conduit à 20 solutions, aux symétries et rotations près ; il faut aussi éliminer les solutions qui comportent des doublets.
Cas de n = 6
Ce cas de figure conduit à un carré à enceinte. On décompose la constante magique choisie, par exemple
M’6 = 165, en une somme de six nombres de base.
Soit M’6 = a + b + c + d + e + f = 25 + 26 + 12 + 33 + 37 + 32 = 165
L’expérience montre que la constante magique choisie et les nombres da base correspondants, doivent satisfaire aux conditions suivantes :
- M’6 doit être divisible par 3, et donc de la forme M’6 = 3 k ;
- Chacun des nombres de base doit être inférieur au tiers « s » de la constante M’6 :
a, b, c, d, e , f < s ( avec s =M’6 / 3 = 55)
On construit d’abord les bordures :
- On place d’abord dans la dernière ligne, suivant les colonnes et les diagonales principales, les compléments à s = 55 des nombres de base de la première ligne ;
- On choisit ensuite :
- deux nombres auxiliaires A et B suffisamment petits ( par exemple A = 2 et B = 4 ) pour égaliser à s = 55 la somme des nombres vis à vis dans les colonnes extrêmes ;
- deux autres nombres auxiliaires P et Q, qui n’apparaîtront pas dans le carré magique final (soit P=4 et Q=3), pour compléter les bordures conformément aux opérations indiquées dans le tableau ci-dessous :
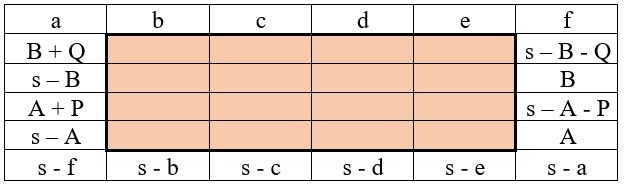
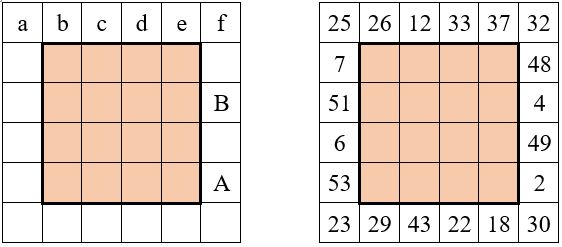
Construction du carré central d’ordre n = 4
Il reste à placer au centre un carré magique d’ordre n = 4 dont on connaît la constante magique :
M’4 = ( 2M’6 / 3 )= 2 * 165 / 3 = 110
On appliquera par exemple, la méthode décrite précédemment, lorsque les nombres de base sont alignés dans la première ligne d’une grille d’ordre n = 4, en rappelant que ce carré central
- ne doit pas comporter lui-même de doublets
- ne doit pas comporter de doublets avec les bordures
- ne doit pas comporter de nombres négatifs.
Ces conditions ne sont pas faciles à remplir simultanément ! Voici une solution :
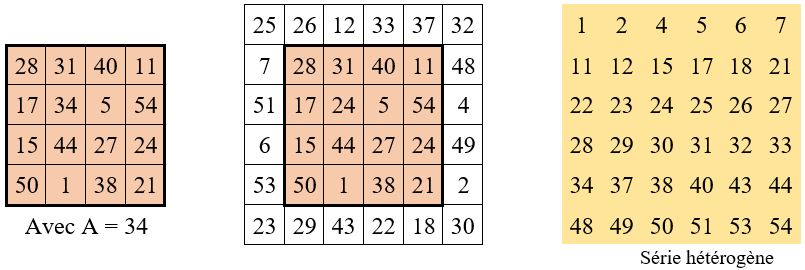
- Cas où M’6 n’est pas un multiple de 3.
Si l’on a M’6 ≠3 k, alors M’6 est de la forme M’6 = 3 k + w. On pourra résoudre le problème en procédant en deux étapes.
- On construit le carré magique à enceinte de constante magique M’6 = 3 k comme carré magique auxiliaire.
- On ajoute le reste w aux termes du carré magique auxiliaire situés sur une permutation figurée diagonale.
Le carré magique résultant est magique, mais il a perdu son caractère de carré magique à enceinte.
Au départ, en principe, plusieurs solutions se présentent ; par exemple on aura, avec M’6 = 167 :
167 = ( 55 x 3 ) + 2
167 = ( 54 x 3 ) + 5
……………………
167 = ( 44 x 3 ) + 35
167 = ( 43 x 3 ) + 38
…………………… ;
On aura intérêt à prendre w suffisamment grand pour éviter les doublets dans le carré numérique final. A noter que des doublets éventuels du carré magique auxiliaire peuvent être supprimés par un choix judicieux de la permutation figurée diagonale.
Il y a théoriquement de nombreuses solutions, mais la chasse aux doublets en élimine beaucoup.
Il faut aussi s’armer de persévérance pour effectuer les différents essais à prévoir (rappelons que l’on dispose de 72 permutations figurées diagonales de 6 éléments).
Les nombres de base de la constante choisie sont placés dans la seconde ligne
Cas de n = 3
On décompose la constante magique choisie M’3 en une somme de trois nombres de base, a, b et c.
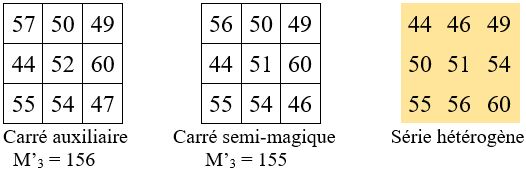
Par exemple M’3 = 156 : M’3 = a + b + c = 44 + 52 + 60
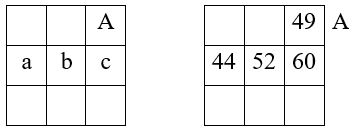
Ce choix et cette décomposition doivent satisfaire aux conditions suivantes :
- On devra nécessairement avoir b =M’3 / 3 = 156 / 3 = 52
- La constante magique choisie M’3 doit être un multiple de 3 : M’3 = 3 k
- On aura alors comme conséquence de 1. ci-dessus : a + c = 2 b.
- Les trois nombres de base devront donc être en progression arithmétique ; ici r = 8.
On choisit alors un nombre auxiliaire A à placer dans un angle, ce qui détermine entièrement le carré, dont les opérations sont résumées dans le tableau ci-dessous et son application numérique, avec A = 49
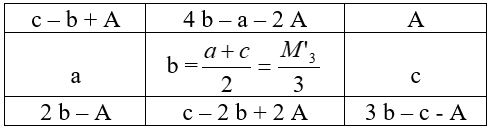
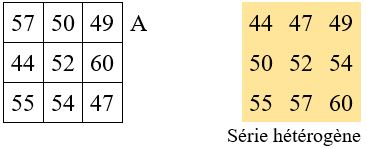
Cas de M’3 3 k.
Lorsque la constante magique choisie n’est pas un multiple de 3, elle est de la forme
M’3 = 3 k + w ( avec w = 1 ou 2 )
On peut ajouter w sur les termes situés sur une diagonale du carré magique obtenu avec M’3 = 3 k, mais on n’obtient qu’un carré semi-magique ( une seule diagonale magique )
Exemple, avec M’3 = 155 = 156 – 1 ; soit w = -1
Cas de n = 4
On décompose la constante magique choisie M’4, en quatre nombres de base ; ainsi par exemple avec M’4 = 110 :
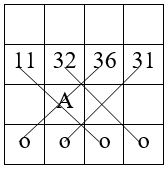
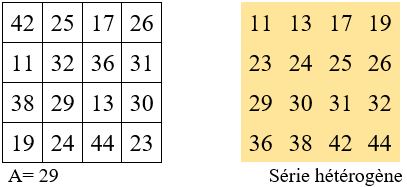
M’4 = a + b + c + d = 11 + 32 + 36 + 31
M’4 doit être divisible par 2 ( pair) : M’4 / 2 = 110 / 2 = 55 = s
On place dans la 4 ème ligne, suivant la marche du fou aux échecs, le complément à s = 55 des nombres de base de la seconde ligne.
On choisit un élément complémentaire A, placé dans une case libre quelconque, qui permet de compléter la grille, conformément aux opérations résumées ci-dessous :

Cas de M’4 impair. M’4 = 2 k 1
On résout le problème en deux temps :
- On construit le carré magique de constante magique M’4 = 2 k, comme carré auxiliaire ;
- On ajoute (ou retranche) l’unité aux nombres situés sur une permutation figurée diagonale.
Exemple , avec M’4 = 111 = 110 + 1
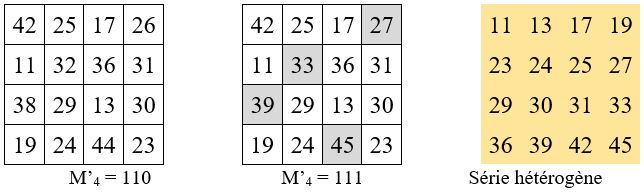
L’essentiel est d’éviter les doublets. Il y a plusieurs solutions (Rappelons que l’on compte 8 permutations figurées diagonales de 4 éléments).
Cas de n = 5
On décompose la constante magique choisie M’5 en cinq nombres de base.
Soit par exemple M’5 = 300 :
La case centrale est alors telle que :
M’5 / 5 = 300 / 5 = 60 = r
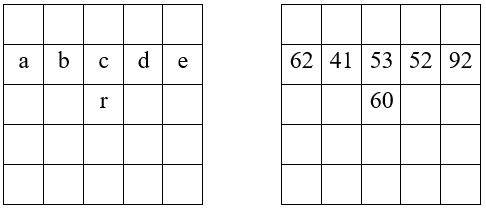
Il faut alors avoir recours à cinq nombres complémentaires A, B, C, D, E, placés dans les bordures, pour compléter la grille, conformément aux opérations résumées dans le tableau ci-dessous.
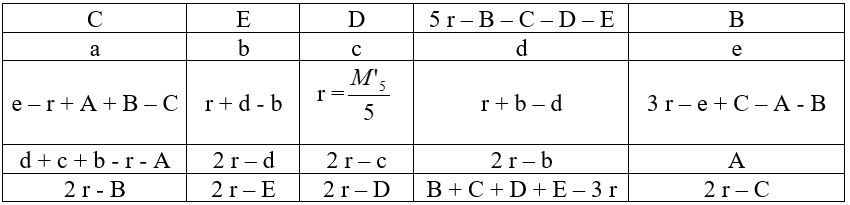
Application numérique
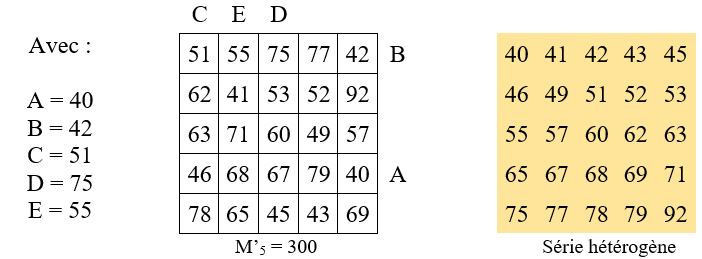
Cas où M’5 ≠5 k
La constante magique choisie M’5 doit être un multiple de 5 : M’5 = 5 k
Si tel n’est pas le cas, M’5 est alors de la forme : M’5 = 5 k + w ( avec w = 1, 2, 3 ou 4)
On pourra résoudre le problème en deux temps :
- On construit tout d’abord le carré magique de constante M’5 = 5 k comme carré auxiliaire ;
- On ajoute ensuite le reste w aux termes de ce carré auxiliaire situés sur une permutation figurée diagonale.
Il y a bien sûr de nombreuses solutions. On aura soin d’éviter tout doublet.
Les nombres de base de la constante choisie sont sur une diagonale principale
Cas de n = 3
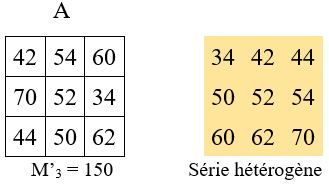
Soit par exemple M’3 = 156 On sait que la case centrale b est égale à b =M’3 / 3 = (a+b+c)/3 = 156/3 = 52
D’où a + c = 2 b. Les trois nombres de base a, b et c doivent être en progression arithmétique.
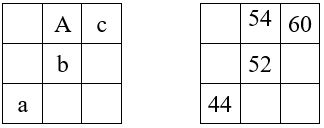
Par exemple avec r = 8 : M’3 = a + b + c = 44 + 52 + 60
Il faut choisir un élément complémentaire A, placé n’importe où dans une case libre, pour compléter la grille, conformément aux opérations résumées dans le tableau ci-dessous (Application numérique. Avec A = 54), pour le placement de A comme indiqué dans les grilles ci-dessus.

Cas de M’3≠3 k
M’3 est de la forme M’3 = 3 k + w ( avec w = 1 ou 2 )
On résout le problème en deux étapes :
- On construit tout d’abord le carré magique de constante M’3 = 3 k comme carré auxiliaire ;
- On ajoute ensuite le reste w aux termes de ce carré auxiliaire situés sur une permutation figurée diagonale.
On obtient cependant un carré semi-magique.
Il y a plusieurs solutions. On aura soin d’éviter tout doublet.
Cas de n = 4
On décompose la constante magique choisie en quatre nombres de base.
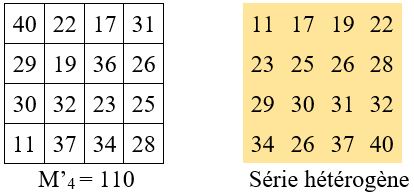
Soit par exemple M’4 = 110
M’4 = a + b + c + d = 11 + 32 + 36 + 31 = 110
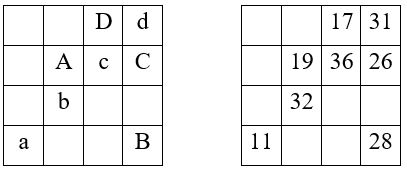
Il faut avoir recours à quatre éléments complémentaires A, B, C, D pour pouvoir remplir la grille, conformément au tableau-résumé ci-dessous :

Application numérique. Avec
A = 19 ;
B = 28 ;
C = 26 ;
D = 17 – M’4 = 110
Remarque.
Il n’y a pas de condition particulière pour M’4, qui peut être paire ou impaire, ni pour les nombres de base a, b, c et d. La présence de doublets et de nombres négatifs, incite cependant à la patience dans les différents essais.
Cas de n = 5.
On décompose la constante magique choisie en cinq nombres de base a, b, c , d, e.
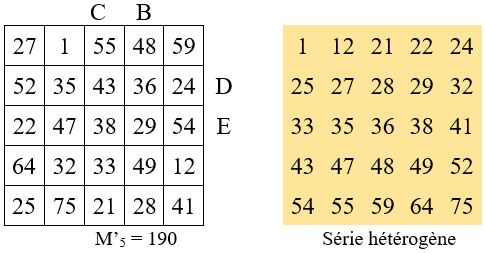
Soit par exemple M’5 = 190.
M’5 = a+b+c+d+e = 25 + 32 + 38 + 36 + 59 = 190
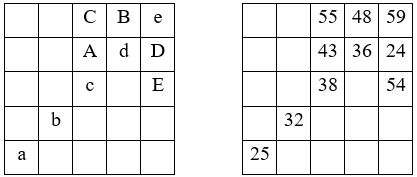
La case centrale est : c =M’5 / 5 = 190/5 = 38
M’5 doit être de la forme M’5 = 5 k.
Il faut avoir recours à cinq éléments complémentaires A, B, C, D, E pour pouvoir remplir la grille. Les opérations sont résumées dans le tableau ci-après.

Application numérique.
Avec A = 43 ; B = 48 ; C = 55 ; D = 24 ; E = 54,
d’une part ;
et, rappelons-le :
a = 25 ; b = 32 ; c = 38 ; d = 36 et e = 59 d’autre part.
Cas de M’5 k
M’5 est de la forme M’5 = 5 k + w (avec w = 1, 2, 3 ou 4)
On résout le problème en deux étapes :
- On construit tout d’abord le carré magique de constante M’5 = 5 k comme carré auxiliaire ;
- On ajoute ensuite le reste w aux termes de ce carré auxiliaire situés sur une permutation figurée diagonale.
On aura soin d’éviter ou de supprimer les doublets.
▶ René Descombes – Les Carrés Magiques – Histoire, théorie et technique du carré magique, de l’Antiquité aux recherches actuelles. Editions Vuibert –Paris, 2000, 500 pp. (avec une bibliographie de plus de 300 titres)
▶ B. Kordiemsky – Sur le sentier des mathématiques – Dunod Editeur – Paris, 2 volumes, 1963.
▶ Jacques Sesiano – Un traité médiéval sur les carrés magiques (manuscrit arabe du X ème siècle, Istambul, 1250) Presses polytechniques et universitaires romanes, Lausanne, 1996, 210 pp. ( texte original arabe, traduction et commentaires de Jacques Sesiano )
▶ Henri Berna – Jeux numériques et magiques dans la troisième dimension – Editions Vuibert-Paris, 2000, 175 pp. ( Le dernier ouvrage de Henri Berna, sur les carrés magiques, et surtout les cubes magiques.)
▶ W.J. Reichmann – La fascination des nombres – Payot Editeur Paris, 1959.
