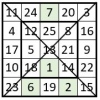
Cette méthode inédite s’applique aux carrés magiques d’ordre impair n = 2k + 1, avec k ≥ 2.
La Méthode des quatre Y pour n = 5
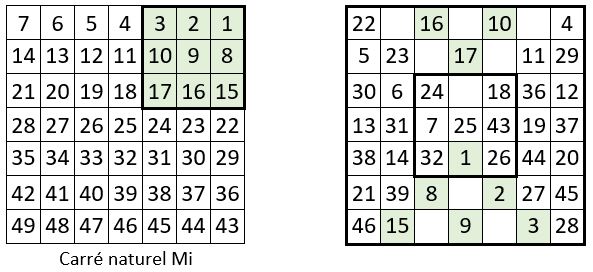
Cette méthode a pour base l’une des formes du carré naturel de même taille, comme catalyseur. Nous prendrons comme catalyseur pour cet exemple le carré naturel « miroir » d’ordre n = 5 (Mi). Voici le déroulement des opérations successives, en cinq étapes :
❶ On place la série des nombres situés sur la médiane horizontale du catalyseur, sur la première diagonale de la grille du carré magique potentiel ; et on place la série des nombres situés sur la médiane verticale de ce même catalyseur, sur la seconde diagonale. Il y a en principe 8 placements possibles, au choix.
Exemple pour notre application n = 5.
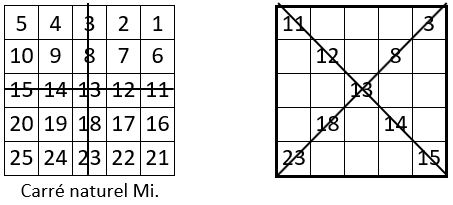
❷ Il reste à placer les 4 x 4 = 16 nombres situés dans les quatre sous-carrés de 4 cases, aux angles du catalyseur : A, B, C, D.

On commence par le sous-carré A, par exemple. On place le nombre situé au sommet A de la grille, soit « 5 », dans l’une des cases libres du sous-carré central de 9 cases de la grille du carré magique potentiel. ( Il y a ainsi un second choix : 4 placements possibles ). Et l’on place le nombre qui lui est diamétralement opposé dans le sous-carré A, soit « 9 », dans la même ligne, le plus loin possible. Les deux nombres qui restent dans ce sous-carré A, c’est-à-dire « 4 » et « 10 », sont à placer symétriquement dans la première colonne ( Il y a deux placements possibles ). A l’issue de cette manip, voici ci-dessous comment se présente la grille du carré magique potentiel : les 4 nombres en cause sont placés en forme de « Y ».
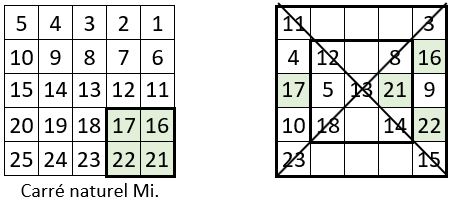
❸ Dans la première colonne, la case vide ne peut être remplie que par « 17 », de manière à donner la constante magique M5 = 65 du carré magique potentiel : ce qui nous amène prendre en considération le sous-carré C diagonalement opposé au précédent A.
On procède alors de la même façon que précédemment, pour placer « 21 » dans la ligne du « 17 », et « 16 » et « 22 » dans la dernière colonne ( Deux placements possibles )
Voici ci-dessus, dans la grille en cours de remplissage, la situation « en Y » des 4 nombres en cause.
❹ On complète alors la seconde ligne par « 25 » ( ce que nous avons fait ), ou bien la quatrième ligne par « 1 ». On procède toujours de la même façon, en plaçant « 19 », et les deux nombres qui restent du sous-carré B dans la première ligne : « 20 » et « 24 » ( Deux placements possibles ). Ci-dessous, la situation après cette manip :
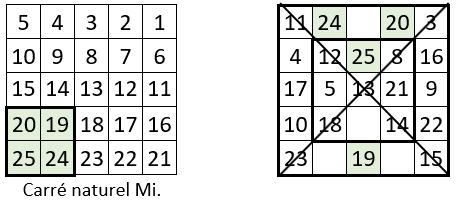
❺ On achève le remplissage de la grille du carré magique potentiel, toujours de la même façon. Le remplissage en « Y » des dernières cases vides s’opère aisément avec les 4 nombres du sous-carré D.
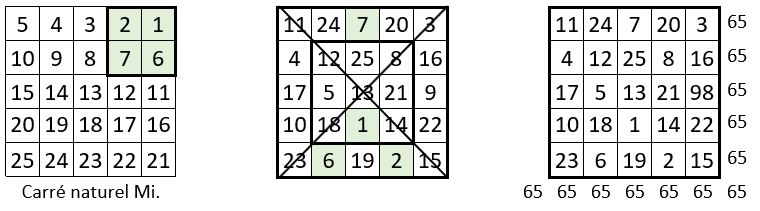
On obtient un carré magique normal, de type associé, de Constante de polarisation P = n2 + 1 =26.
La procédure itérative de cette méthode est claire et très apparente.
Et bien sûr il y a des « choix » à faire. Heureusement d‘ailleurs, cela nous permet de tenter une approximation du dénombrement théorique des grilles possibles pour n = 5 :
N5 = 8 x 4 x 2 x 2 x 2 x 2 = 512. Mais ces grilles ne sont sans aucun doute pas toutes magiques !
Et l’on peut adapter cette méthode, avec beaucoup de patience, à la construction des carrés magiques d’ordre supérieur n = 7, n = 9, . . .
Cette méthode ne semble n’avoir jamais été proposée à ce jour, à notre connaissance.
La Méthode des quatre Y pour n = 7
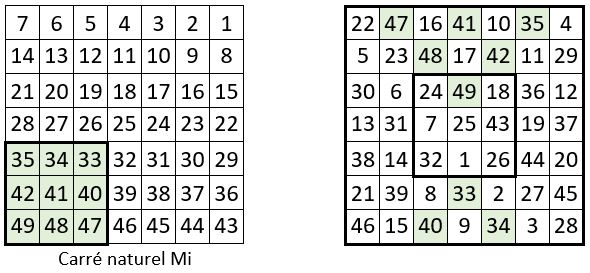
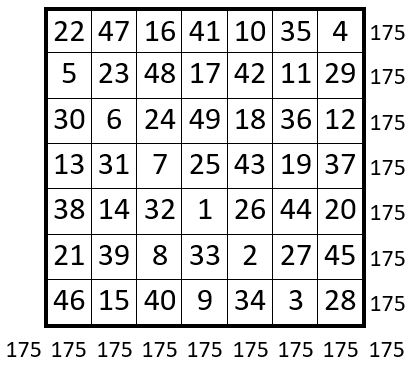
Voici ci-dessous les cinq manips successives. C’est un peu moins simple. On obtient un carré magique normal de type associé, de Constante de polarisation P = n2 + 1 = 50.
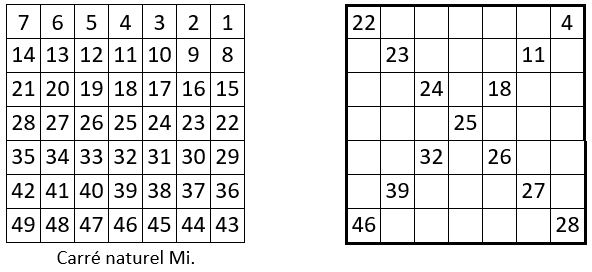
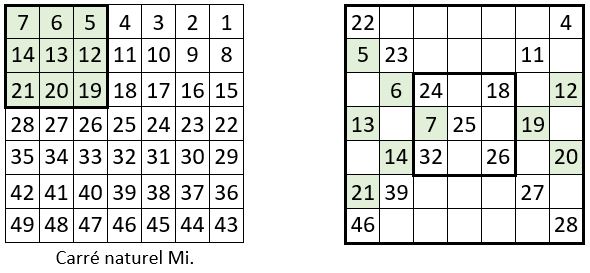
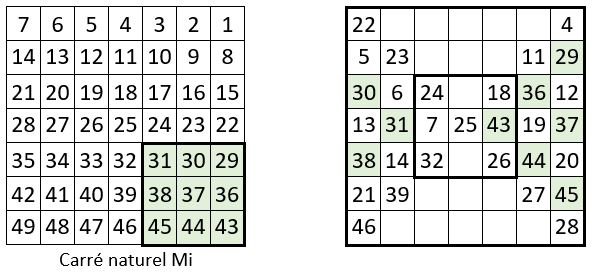
L’évolution du concept « Y »
Le concept « Y » évolue de la façon suivante, pour les ordres n = 5, 7 et 9 :
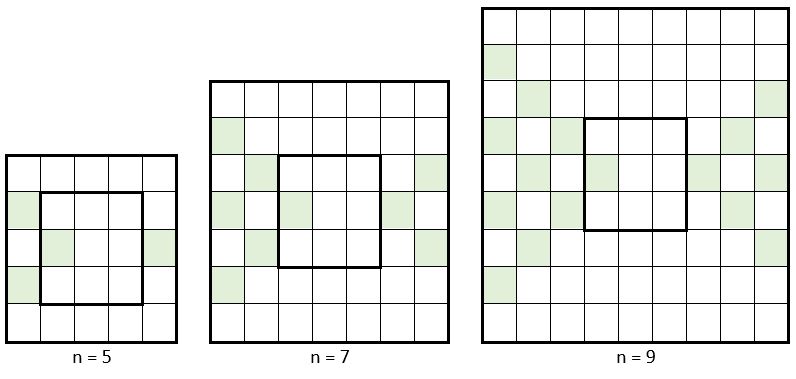
Or, a vrai dire, les carrés magiques d’ordre n = 5 et n = 7 ci-dessus, construits en application de la Méthode des quatre Y, correspondent aux carrés magiques de même ordre qui figurent parmi les sept carrés magiques planétaires présentés par Cornélius Agrippa de Nettesheim dans son ouvrage De Occulta Philosophia, paru à Cologne en 1533. Cette correspondance existe également pour l’ordre n = 9, comme on peut le vérifier. Rappelons en passant que ce carré magique d’ordre n = 9 correspond aussi au carré magique inséré par le pape Léon III dans l’édition originale de son Enchiridion, rédigé vers l’an 795
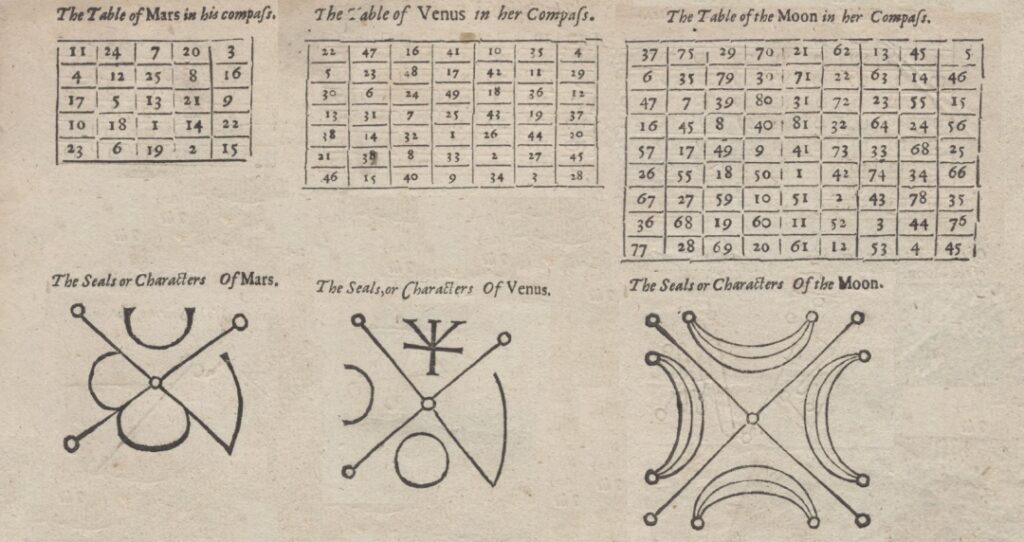
Agrippa n’a pas dévoilé de façon explicite les méthodes de construction de ses sept carrés magiques planétaires, mais il a donné, pour chaque carré, un schéma censé représenter cette construction.
Le général Eutrope Cazalas (1864-1943), dans son ouvrage : Carrés magiques au degré n , a bien décrypté les méthodes d’Agrippa pour la construction des carrés magiques d’ordres : n = 3, 4, 6 et 8.
Il n’a cependant pas décrypté la méthode de construction d’Agrippa pour les ordres
n = 5, 7 et 9, méthode restée mystérieuse jusqu’à ce jour, semble-t-il.


Or la méthode décrite ci-dessus, se rapproche sensiblement des schémas d’Agrippa von Nettesheim.
On serait alors tenté d’augurer que la Méthode des quatre Y, correspond à la méthode utilisée par Henri Cornelius Agrippa, en 1533, pour construire ses carrés magiques planétaires d’ordre n = 5, 7 et 9 . . .
Les méthodes de construction des sept carrés magiques d’Agrippa seraient ainsi et enfin toutes dévoilées, cinq siècles après l’édition de la De Occulta Philosophia libri tres.
Henri Corneille Agrippa – La magie céleste – Traduit et présenté par Jean Servier – Editions Berg International 1981, (Voir en particulier les tables des pp. 130-134.)
Henry Cornelius Agrippa – Three Books Of Occult Philosophy, le livre complet sur Internet Archive
Général Cazalas – Carrés magiques au degré n – Hermann Editeur 1934
René Descombes – Le Carré magique du Pape Léon III – Bib Num Septembre 2014
René Descombes – Les carrés magiques planétaires d’Agrippa revisités – Bib Num Janvier 2019
Lucien Gérardin – Les Carrés magiques – Mystérieuses harmonies des nombres – Editions Dangles 1986