Sommaire
La Méthode d’Édouard Lucas. Cas de n = 3.
La constante magique choisie M’3, doit être un multiple de 3, soit de la forme M’3 = 3 K.
| K + A | K – (A + B) | K + B |
| K – (A – B) | K | K + (A – B) |
| K – B | K + (A + B) | K – A |
On choisit alors deux auxiliaires A et B suffisamment petits, et l’on effectue les opérations indiquées par Edouard Lucas dans le tableau ci-dessus.
Le carré numérique obtenu est magique par construction.
Exemple
M’3 = 63 = 3 x 21 ; K = 21.
Soit les auxiliaires A = 3 et B = 4. avec A + B = 7 et A – B = – 1
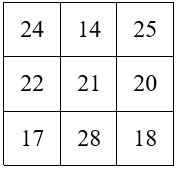
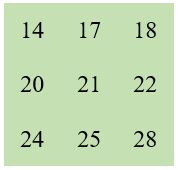
On remarque dans le tableau littéral comme dans le carré numérique, que tout alignement qui passe par la case centrale, est composée de 3 termes en progression arithmétique. Cette propriété est générale pour tous les carrés magiques d’ordre 3.
Il y a de nombreuses solutions, sous conditions que M’3 soit un multiple de 3, et que, pour le choix des auxiliaires A et B, on ait A + B < K, afin que tous les termes du Carré Magique soient > 0.
La Méthode de Reichmann. Cas de n = 3.
Dans cette méthode, donnée par W. J. Reichmann, dans son ouvrage « La fascination des nombres », Payot 1959, pp. 156-166 (Les Carrés magiques), la constante magique choisie M’3, doit être un multiple de 3, et donc de la forme M’3 = 3 K.
On choisit trois nombres X, Y et Z, tels que X + Y + Z = K
Et l’on effectue les opérations indiquées dans le tableau ci-dessous.
| 2 X + Y + Z | Z | X + 2 Y + Z |
| 2 Y + Z | X + Y + Z = K | 2 X + Z |
| X + Z | 2 X + 2 Y + Z | Y + Z |
Exemple
M’3 = 183 = 3 x 61 ; K = 61
avec K = X + Y + Z = 5 + 9 + 47 = 61
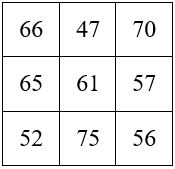
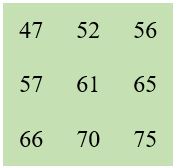
Nota. Indépendamment du choix de M’3, la Méthode Reichmann permet de construire un carré magique à partir de trois nombres donnés, X, Y et Z. On aura M’3 = 3 ( X + Y + Z ).
La Méthode de Bergholtz. Cas de n = 4.
Cette méthode a été rapportée par Boris Kordiemsky, en 1963.
Soit M’4 la constante magique choisie. On choisit quatre nombres a, b, c et d (dits nombres de base) tels que M’4 = a + b + c + d
Soit M’4 la constante magique choisie. On choisit quatre nombres a, b, c et d (dits nombres de base) tels que
M’4 = a + b + c + d
On place ces quatre nombres dans les cases centrales de la grille auxiliaire I :
| -A | A+C | B-C | -B |
| A-D | -A+D | ||
| -B+D | B-D | ||
| B | -A-C | -B+C | A |
Rappelons que dans tout carré magique d’ordre n = 4, la somme des 4 cases centrales, et celle des 4 cases angulaires, sont égales à la constante magique. Les termes a, b, c, d sont à leur place définitive.
On complète alors la grille I en carré latin. Dans la grille auxiliaire II, on place quatre nombres arbitraires A, B, C, D dans les cases périphériques, seuls ou groupés deux à deux, de telle façon que la somme des cases extrêmes des lignes et colonnes médianes, et des diagonales principales, soit nulle
On additionne case par case les deux grilles auxiliaires I et II :
la grille III est magique, de constante linéaire
M’4 = a + b + c + d
| a – A | c + A + C | b + B – C | d – B |
| d + A – D | b | c | a – A + D |
| c – B + D | a | d | b + B – D |
| b + B | d – A – C | a – B + C | c + A |
Application numérique
a = 24 ; b = 9 ; c = 21 ; d = 30 avec A = 14 ; B = 10 ; C = 12 ; D = 5.
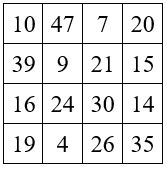
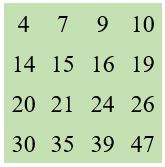
Remarques.
Le choix des nombres a, b, c, d et A, B, C, D, peut produire des doublets dans la grille III. Il faut alors modifier le choix en cause.
Les nombres auxiliaires A, B, C, D n’apparaissent pas dans le carré final. Ils jouent le rôle d’un catalyseur.
Si l’on choisissait M’4 = 34 = M4= a + b + c + d, soit la constante magique d’un carré magique normal d’ordre n = 4, c’est par le plus grand des hasards que l’on obtiendrait un carré magique normal, utilisant tous les entiers consécutifs de 1 à n2.
La méthode de Yu I. Ermakov. Cas de n = 4.
Cette méthode a été rapportée par Boris Kordiemsky, en 1963.
On choisit les « nombres de base » a, b, c, d, tels que M’4 = a + b + c + d, que l’on place dans les cases angulaires de la grille auxiliaire I : les nombres a, b, c, d, sont à leur place définitive.
On complète la grille auxiliaire I en carré latin normal..
| A+B | -A-B | ||
| C-D | -A-C | A-C | C+D |
| -C+D | -A+C | A+C | -C-D |
| A-B | -A+B |
On additionne case par case les deux grilles auxiliaires I et II ;
la grille III est magique, et de constante linéaire
M’4 = a + b + c + d.
| a | b + A + B | c – A – B | d |
| c + C – D | d – A – C | a + A – C | b + C + D |
| d – C + D | c – A + C | b + A + C | a – C – D |
| b | a + A – B | d – A + B | c |
Application numérique
a = 28 ; b = 16 ; c = 30 ; d = 25 ; avec A = 10 ; B = 7 ; C = 14 ; D = 9.
M’4 = 99 = 28 + 16 + 30 + 25
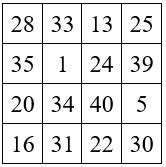
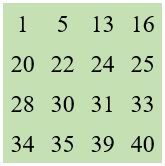
Remarques.
Les remarques pour la Méthode de Bergholtz précédente, sont également applicables pour la méthode de Ermakov.
Méthode de Labosne-Méziriac
Rappelons tout d’abord la relation donnant la constante magique par la méthode de Labosne-Méziriac, en fonction des « nombres de base »à caractère spécial, que sont a, b, c d,… :
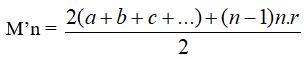d’où l’on tire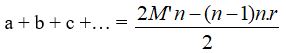 
On décompose donc le second membre de l’égalité ci-dessus en une somme de n nombres entiers a + b + c +…, dits « nombres de base ».
On place alors ces nombres de base dans les créneaux d’une grille crénelée, conformément aux dispositions des schémas ci-dessous (n=3, 7 et 7) :
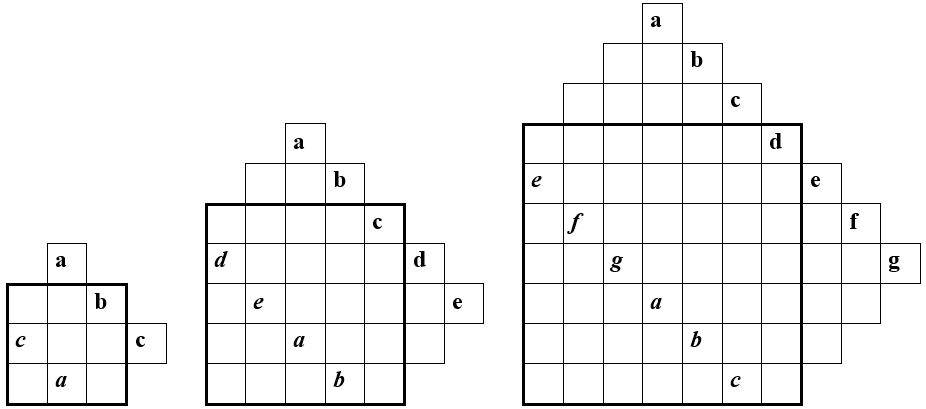
On complète les alignements perpendiculaires par les termes d’une progression arithmétique de raison r = k n :
a + r ; a + 2r ; a + 3r ; …
b + r ; b + 2r ; b + 3r ; …
Le nombre médian de la suite impaire des « nombres de base » est à sa place définitive dans la dernière case de la première ligne de la grille d’ordre n. On retrouve les autres nombres de base dans cette grille (cf . lettres en italique dans les schémas ci-dessus).
Application numérique.
Soit M’5 = 140, avec n = 5 ; et r = k n = 2 . 5 = 10 On a donc :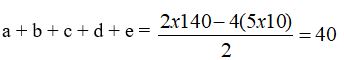
On peut décomposer ce résultat ainsi, par exemple : a + b + c + d + e = 5 + 3 + 8 + 10 + 14 = 40
Et l’on peut construire le carré magique ci-dessous, de constante magique M’5 = 140 :
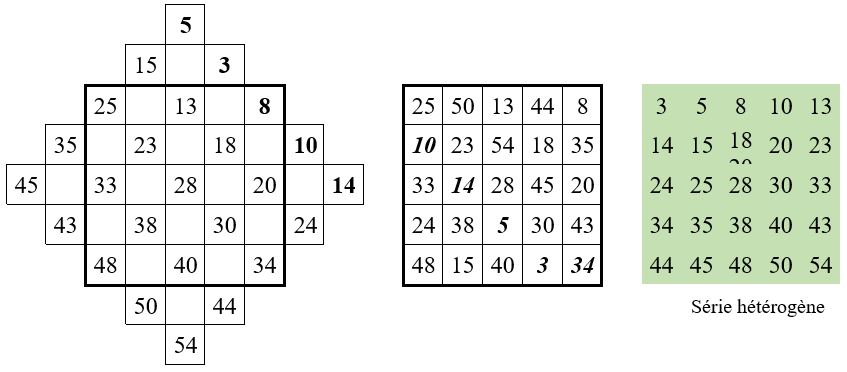
On peut construire, avec la même série de « nombres de base », autant de carrés magiques de même constante magique, qu’il y a de permutations de ces nombres de base, c’est-à-dire n !.
Conditions de magie.
La somme des nombres de base, qui résulte du choix de la constante magique, ne peut pas être décomposée arbitrairement.
On doit en effet observer les conditions suivantes :
- Dans la suite des nombres de base, le nombre médian doit être la moyenne arithmétique desdits nombres de base. Ainsi dans notre exemple
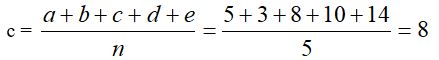
Il faut donc que la somme a + b + c + d… soit un multiple de n. - Le coefficient k de la raison r = k n des alignements perpendiculaires, doit vérifier la relation k=(n – 1) / 2
- Les différences ∆ entre les nombres de base, consécutifs ou non, doivent être différentes de r = k n :
∆1, ∆2, ∆3… ≠k n
Si l’on respecte ces conditions, on obtient toujours un carré magique ; si l’on transgresse l’une ou l’autre de ces conditions, on risque d’obtenir un carré parsemé de doublets, et/ou un carré semi magique. Mais ce risque n’est pas systématique.
Contre-exemple
Avec n = 5 et k = 3 donc k ≠(n -1) / 2
Soit M’5 = 185, avec n = 5, et r = k n = 3 x 5 = 15, On a donc :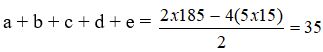 
On peut décomposer ce résultat ainsi : a + b + c + d + e = 2+5+7+10+11 = 35
Et l’on peut construire le carré numérique ci-dessous, qui est bien magique : M’5 = 185.
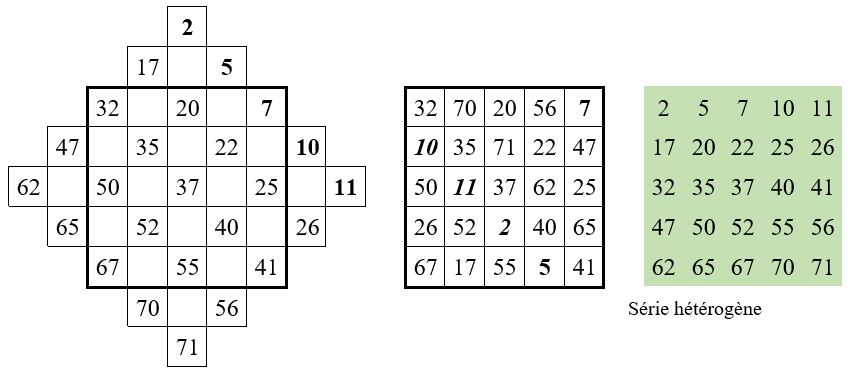
▶ Claude-Gaspard Bachet de Méziriac (1612) – Problèmes plaisants et délectables qui se font par les nombres – 1874 -Edition revue, simplifiée et augmentée par A. Labosne, Professeur de Mathématiques – Editions Blanchard – Paris, 244 pp. pour le nouveau tirage de la 5ème édition, 1993
▶ Biographie de Claude-Gaspard Bachet de Méziriac sur ce blog
▶ Construction des Carres Magiques par la Méthode de Bachet de Méziriac sur ce blog
▶ Boris Kordiemsky – Sur le sentier des mathématiques – Dunod Editeur – Paris, 2 volumes, 1963.