On se propose de rechercher comment on peut construire un carré magique, en nombres discontinus, lorsqu’on se donne a priori son ordre n et sa constante magique M’n.
Rappel de quelques propriétés générales des carrés magiques.
Sommaire
Propriété des quatre opérations
On n’altère pas la magie d’un carré magique lorsque l’on augmente ou diminue tous ses termes d’un même nombre w, ni lorsque l’on multiplie ou divise lesdits termes par un même facteur.
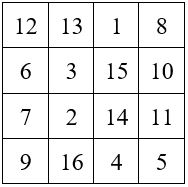
M4 = 34
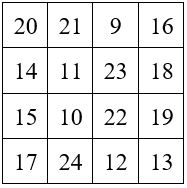
M’4 = 34 + (4 x 8) = 66
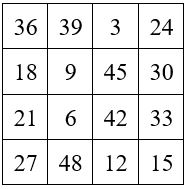
M’4= 34 x 3 =102
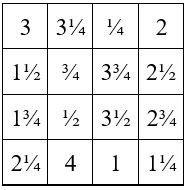
M’4 = 34 / 4= 8 ½
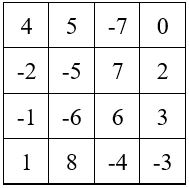
M’4 = 34 – (4 x 8) = 2
Remarque.
Cette propriété fut utilisée notamment autrefois pour la confection des amulettes, des talismans en forme de carré magique, que les belles de jadis suspendaient au cou ou portaient au poignet ou à la cheville, en guise de pendentif, gourmette, bracelet. Les kabbalistes donnaient aux carrés magiques le nom de « Kamea », que l’on peut traduire par « amulette » ; le mot « camée » en dérive directement.
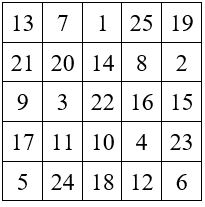
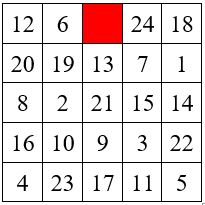
Afin de ménager un trou pour faire passer la chaînette du talisman métallique, on enlève une unité à tous les termes du carré magique de gauche. Le carré numérique de droite reste magique, avec pour constante linéaire M’5 = 65 – 5 = 60 ( termes de zéro à 24).
L’opération n’est pas répétitive sur le carré ainsi modifié, c’est-à-dire sur le talisman.
Propriété des permutations figurées diagonales
On n’altère pas la magie d’un carré magique d’ordre n, lorsque l’on augmente ou diminue d’un même nombre w les n termes situés sur une permutation figurée diagonale.
Exemples. On ajoute w = 20 aux termes situés sur les cases ombrées.
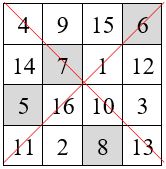
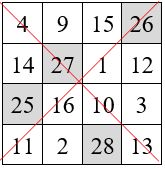
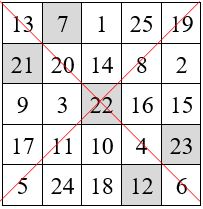

Propriété des permutations figurées diagonales maximum
On constate dans certains carrés magiques normaux d’ordre n, que les n derniers termes de la série « 1 – n2 » occupent les cases d’une permutation figurée diagonale, que l’on nomme alors permutation figurée diagonale maximum.
Lorsque l’on augmente d’un même nombre w les n termes d’un tel carré magique situés sur une permutation figurée diagonale maximum, on n’altère pas la magie du carré magique en cause, et en outre, on est sûr de ne pas générer de doublets dans le carré magique résultant.
Cette propriété importante, trouvera son application dans différentes méthodes de construction présentées ici.
Conventions et symboles
n = ordre du carré magique, ou nombre de cases par côté de la grille carrée de n2 cases.
Mn ou Mn = Constante linéaire magique du carré magique normal d’ordre n.
M’n ou M’n = Constante linéaire magique d’un carré numérique d’ordre n, en nombres discontinus, ou en progression non régulière. C’est, dans ces pages, la constante choisie » a priori « .
Un certain nombre de méthodes sont présentées dans les articles de la catégorie Constante linéaire à priori
