Méthode multiplicative
La relation classique de la division d’un nombre entier a par un nombre entier b est : a = b . q + r
q étant le quotient et r le reste.
Posons : a = M’n et b = Mn
Effectuons alors la division : M’n = Mn . q + r
La construction du carré magique de constante M’n à partir d’un carré magique auxiliaire de constante Mn, s’effectue de la manière suivante : On multiplie chaque terme du carré auxiliaire d’ordre n, par le quotient q, et l’on répartit le reste r sur chaque ligne de cases, c’est-à-dire en augmentant chaque terme de la quantité r / n
Exemple pour n = 3
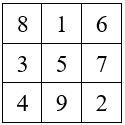
Le Lo Shu ; M3 = 15
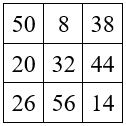
M’3 = 96

Soit M’3 = 96 : On aura : 96 = (15 x 6 ) + 6
On multiplie chaque terme du carré auxiliaire par q = 6, et ensuite on ajoute encore à chaque terme la quantité
r / n= 6 / 3 = 2
Exemple pour n = 4.
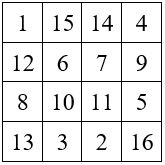
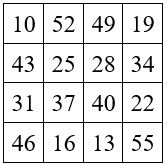

M’4 = M4 + r avec M4 = 34 et M’4 = 130 130 = ( 34 . 3 ) + 28
Facteur multiplicatif : q = 3 et Facteur additif : r / n = 28 / 4 = 7
On ne peut pas donner à M’n n’importe quelle valeur si l’on raisonne en nombres entiers : pour permettre la répartition du reste r dans chaque ligne de n cases, ce reste r doit être un multiple de n.
Variante : Au lieu de répartir le reste r sur les n termes de chaque ligne, on peut ajouter ce reste en une seule fois, aux n termes d’une permutation figurée diagonale.
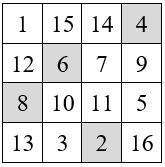
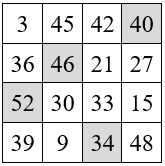
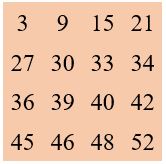
avec le Facteur multiplicatif : q = 3 et le Facteur additif : r = 28
Il y a 8 solutions, qui correspondent aux 8 permutations figurées diagonales d’ordre 4.
On peut alors donner à M’n une valeur quelconque.
Variante : On peut aussi admettre des nombres fractionnaires ou des nombres négatifs dans le carré magique que l’on se propose de construire.
On obtient alors un carré magique avec n’importe quelle valeur de M’n.
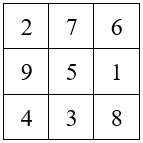
Le Lo Shu ; M3 = 15
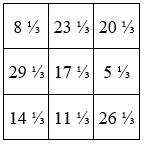
M’3 = 52

Soit M’3 = 52 , On aura M’3 = M 3 . q + r ; et 52 = (15 x 3) + 7
avec le Facteur multiplicatif q = 3 et le Facteur additif r / n = 7 / 3 = 2 + ⅓
Méthode du quotient
(ou Méthode du nombre additionnel uniforme)
On augmente d’un même nombre tous les termes du carré auxiliaire.
On choisit la nouvelle constante M’n, et l’on répartit la différence ∆ entre cette nouvelle constante M’n, et la constante magique Mn du carré magique auxiliaire normal, sur les n termes de chaque ligne (ou colonne) du carré auxiliaire.
Soit à répartir le nombre additionnel élémentaire w=(M’n – Mn ) / n = ∆ / n
Exemple pour n = 3 :
prenons le Carré auxiliaire (Lo Shu) : M3 = 15 et soit M’n = 69
donc w=(69 – 15 ) / 3 = 18
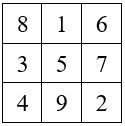
Le Lo Shu : M3 = 15
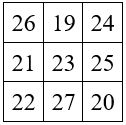
M’3 = 69

croissante homogène (r=1)
Lorsque la quantité à répartir ∆= M’n – Mn est divisible par n, on obtient un carré magique en nombres entiers > 0. Mais cela limite le choix de la nouvelle constante magique M’n.
En effet ∆= M’n – Mn divisible par n, est donc de la forme ∆= k.n
avec Mn =n(n2+1)/2 d’ou M’n =k n + n(n2+1)/2
On en déduit k = w. Le tableau des valeurs de M’n = f (n, k) peut ainsi être présenté :
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 18 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 3 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 51 | 57 | 69 | 75 |
| n = 4 | 38 | 42 | 46 | 50 | 54 | 58 | 62 | 66 | 70 | 74 | 82 | 90 | 106 | 114 |
| n = 5 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 125 | 135 | 155 | 165 |
| n = 6 | 117 | 123 | 129 | 135 | 141 | 147 | 153 | 159 | 165 | 171 | 183 | 195 | 219 | 231 |
Pour n impair, les valeurs de M’n sont des multiples de n
Pour n pair, les valeurs de M’n – (n/2) sont des multiples de n
Mais si l’on admet des nombres fractionnaires, ou des nombres négatifs dans le carré magique que l’on veut construire, alors M’n peut être quelconque.
Exemple avec n = 4 et des nombres fractionnaires.
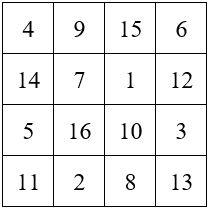
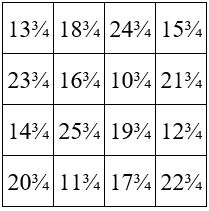

avec M’4 = 73 et w= (73-34)/4 = 9 +¾
Exemple avec n = 4 et des nombres négatifs.
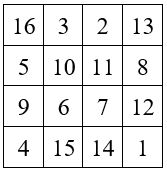
M4 = 34
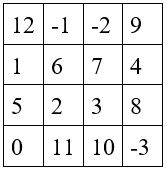
M4 = 18

avec M’4 = 18 et w= (18-34)/4 =-4
