Cette méthode est basée sur la » marche » du cavalier au jeu des échecs. Elle a été mise au point par le mathématicien bâlois Leonhardt Euler (1707-1783), notamment dans une communication intitulée « De quadratis magicis » (StPetersbourg, 1776)


Rappelons qu’à partir d’une case donnée de l’échiquier, le cavalier peut de déplacer de 8 façons différentes, selon 8 « marches » orientées de manière différente.
La mise en place de la suite des entiers de 1 à n2 dans la grille de n2 cases (n impair), est faite en application de deux règles de marche ou de cheminement.
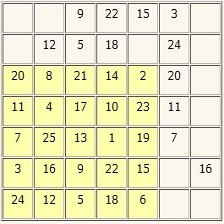
- Marche principale – A partir d’une case-départ quelconque, on suit l’une des 8 marches du Cavalier. Par exemple deux pas vers le haut, un pas vers la droite (-2,1).
- Marche secondaire – Lorsque l’on tombe sur une case déjà occupée (ce qui se produit aux étapes n, 2n, 3n, …(n-1) n ), on fait par exemple deux pas vers la droite sur la même ligne, pour trouver une case libre, soit le déplacement (0,2). On reprend alors la même marche principale du Cavalier (-2,1).
Lorsque l’on sort de la grille de base n x n, il faut bien repérer la position » hors-case » à laquelle on aboutit sur la grille virtuelle contiguë, et superposer cette position » hors-case » à la grille de base.
Dans l’exemple ci-dessus, on a placé ces » hors-cases » dans les grilles virtuelles adjacentes correspondantes, pour bien montrer la réintégration de ces hors-cases.
On peut ainsi établir la fiche signalétique de l’exemple ci-dessus :
Ordre de la grille n = 5
Case-départ ( 3,4 )
Marche principale ( -2,1 )
Marche secondaire ( 0,1 )
Constante magique M5 = 65
Ces caractéristiques définissent parfaitement le carré magique en cause.
Précisons que la » case-départ » peut être placée de façon arbitraire ; cependant le carré numérique obtenu n’est pas toujours un carré magique, mais peut être semi-magique.
La progéniture du Cavalier.
- Toutes les cases conviennent comme case-départ. On peut donc construire n2 carrés numériques (magiques ou semi-magiques) avec la même marche principale et la même marche secondaire.
- Il y a 8 marches possibles pour le Cavalier. De chaque case-départ on peut donc construire 8 carrés numériques avec la même marche secondaire.
- Pour la marche secondaire, le problème se pose après une première étape » n « . On peut supposer qu’à ce moment, toute case libre convient comme » terminal » de la marche secondaire. Dans cette hypothèse on aurait n2 –n = n (n-1) marches secondaires possibles.
- Au total le nombre de solutions N serait donné par la relation : N = 8 n2 [n ( n-1)] = 8 n3 (n-1). Ainsi pour n = 5, on a N = 4 .000 et pour n = 7, on a N = 16.464
Méthodes » variantes » de la Méthode du Cavalier.
Pour les ordre n impairs, on peut concevoir nombre de méthodes » variantes » sur le principe général de la Méthode dite du Cavalier, par cheminement régulier.
En voici quelques unes, considérées comme classiques, résumées dans le tableau ci-après :
| Désignation (n impair) | Case-départ | Marche principale ( i, j ) | Marche secondaire ( i, j ) |
|---|---|---|---|
| Bachet de Méziriac Moschopoulos I | Au-dessous de la case centrale | ( 1, 1 ) | ( 2, 0 ) |
| De La Loubère (1691) | Quelconque | ( 1, 1 ) ( 1, 1 ) | ( 2, 0 ) ( 1, 0 ) |
| Moschopoulos II (Carré panmagique) | Case centrale de la 1ère ligne ou quelconque | ( 2 ,1 ) | ( 4,0 ) |
| Jacques Bouteloup (1991) | Quelconque | ( 3, 1 ) ( 2, 3 ) | (-6, 0 ) ( 1, 0 ) |
