François Spinula (Francisci Spinulae), un père jésuite, décrit dans son ouvrage :
De intercalandi ratione corrigenda & de tabellis quadratorum numerorum à Pythagoreis dispositorum (1562),
une méthode de construction des carrés magiques normaux d’ordre pair, de la forme n = 4k.
On peut présenter cette méthode de la manière suivante.

Exemple pour n = 4. M4 = 34
▶ On part du carré naturel N ; on sait que dans le carré naturel pair ou impair, les diagonales principales sont magiques ; on ne touche pas aux diagonales principales.
▶ On permute les nombres diamétralement opposés, c’est-à-dire les cases contiguës des extrémités de la croix centrale.
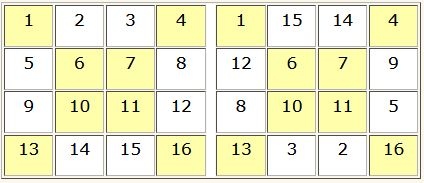
Application pour n = 8. M8 = 260
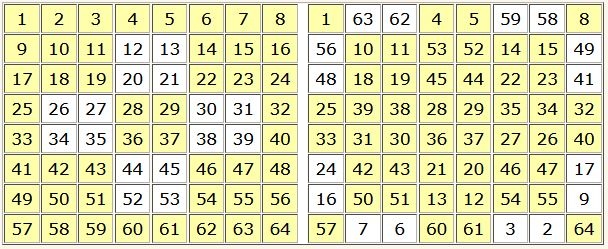
▶ On ne touche pas aux diagonales principales.
▶ On permute les nombres diamétralement opposés des carrés de 2×2, aux extrémités de la croix centrale de 6×6.
▶ On permute les nombres diamétralement opposés des 4 groupes de 2 cases en équerre aux angles de la grille de 8 x 8.
▶ On ne touche pas aux autres nombres, les couples situés aux extrémités de la croix centrale de 8 x 8.
