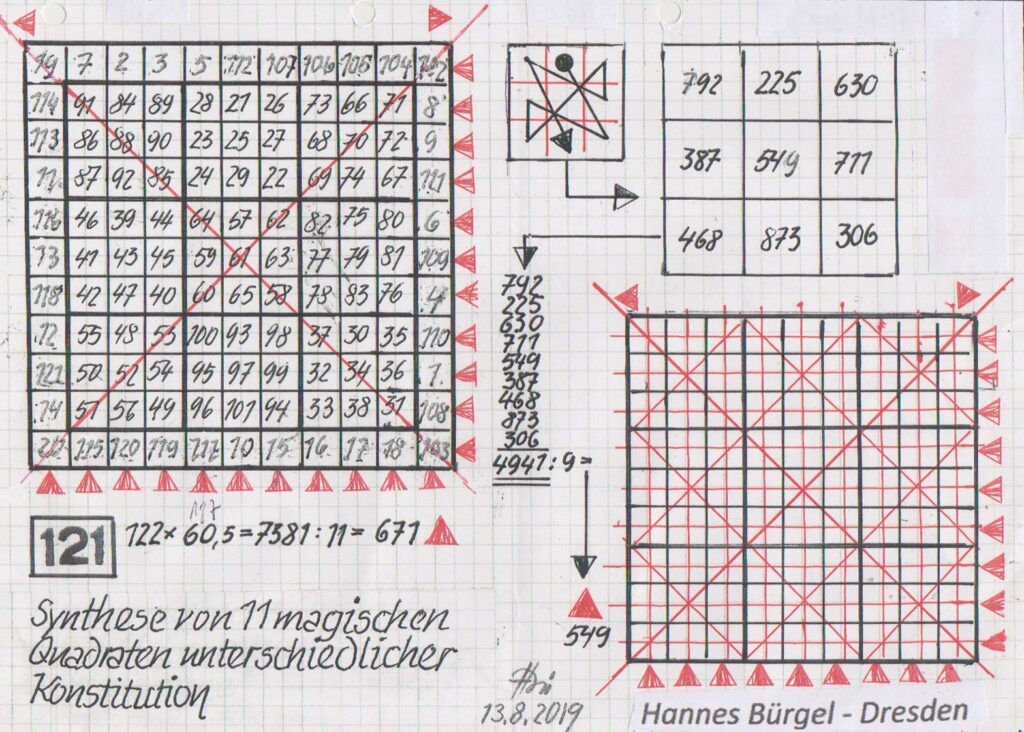
Introduction
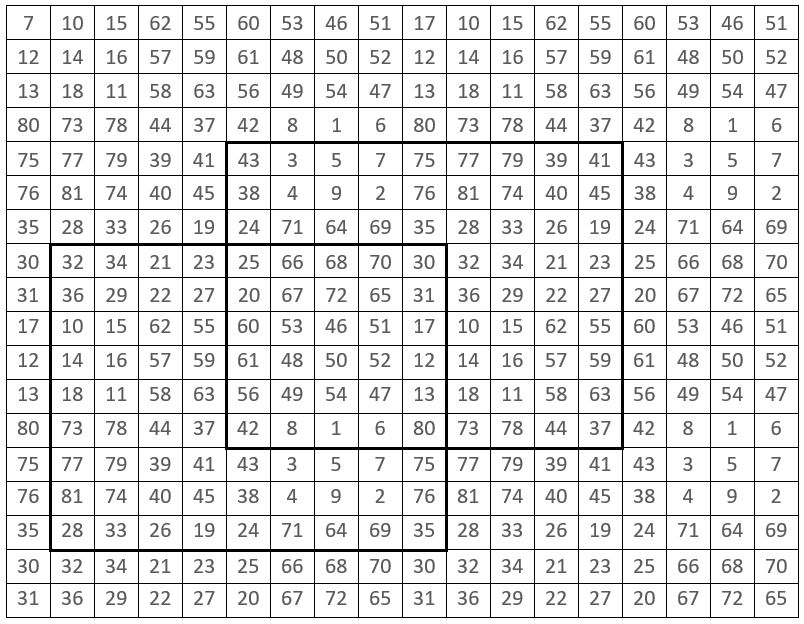
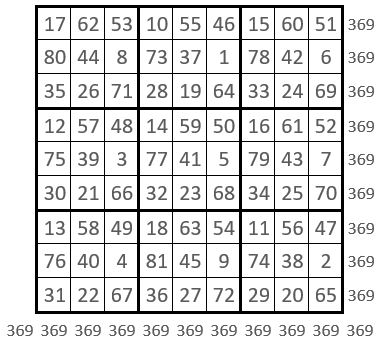
On considère la grille d’ordre n = 9, de 92 = 81 cases, comme constituée de 9 sous-carrés d’ordre n = 3, de 32 = 9 cases.
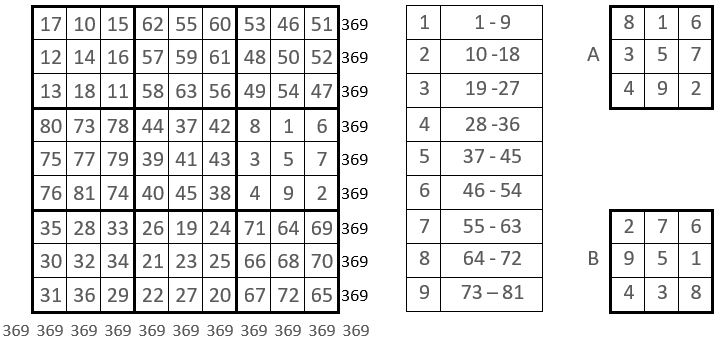
On construit 9 sous-carrés d’ordre n = 3, avec les 9 séquences consécutives de 9 termes de la série ( 1 – 81 ), conformément à la polygraphie de l’une des formes du Lo Shu (A), pris comme catalyseur.
Et l’on place ces 9 sous-carrés dans la grille d’ordre n = 9, conformément à la polygraphie de l’une des formes du Lo Shu (B), en principe différente de (A).
La grille d’ordre n = 9 obtenue, est un carré magique normal d’ordre n = 9, et de Constante magique M9 = 369.
Propriétés
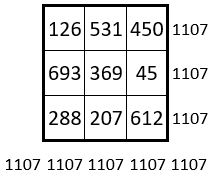
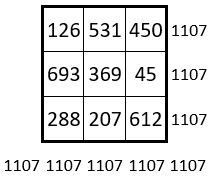
❶Tout d’abord, les sommes des termes dans chacun des 9 sous-carré d’ordre n = 3, forment elles-mêmes un carré magique ( Ci-contre ), non normal, de Cte magique M’3 = 1107. Et on observe : M’3 = 1107 = 3 x 369 = 3 M9.
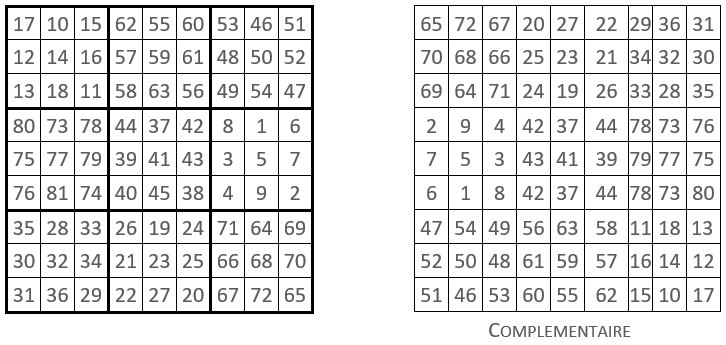
❷Ce carré magique d’ordre n = 9 est de type associé : la somme des couples complémentaires est constante et égale à n2 + 1 = 81 + 1 = 82, dite constante de polarisation, soit le double de la case centrale.
❸Alors, comme c’est le cas de tout carré magique de type associé, notre super carré magique d’ordre n = 9 est autocomplémentaire ou autodual : rappelons que lorsque l’on remplace chaque terme d’un carré magique normal d’ordre « n » par son complément à ( n2 + 1 ), on obtient un carré magique de même constante magique, dit complémentaire. Lorsque le carré magique obtenu coïncide, après rotation, avec le carré initial, ce dernier est alors dit autocomplémentaire. C’est bien le cas de notre super carré magique d’ordre n = 9 :
❹Dans le tapis de ce carrés magiques d’ordre n = 9, , toute fenêtre d’ordre n = 9 de n2 = 81 cases, correspond à un carré magique d’ordre n = 9, de Constante magique M9 = 369.
Dans ce seul tapis, on peut ainsi représenter 9 x 9 = 81 carrés magiques d’ordre n = 9 différents.
Construction
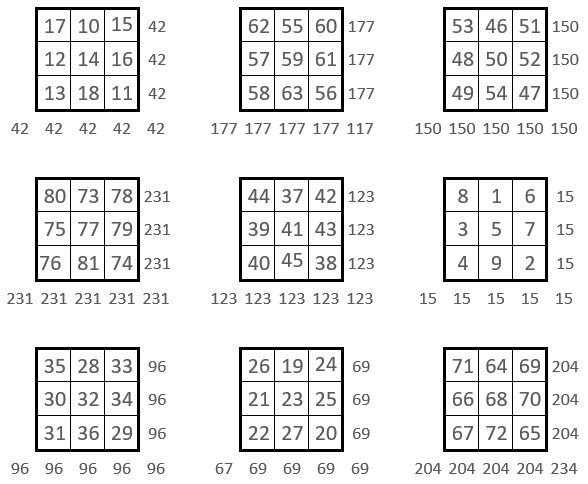
On se propose ensuite de construire la série des carrés numériques, constitués par les termes homologues des 9 sous-carrés d’ordre n = 3, de la grille d’ordre n = 9 initiale.
Voici les 9 carrés ainsi constitués : ce sont des carrés magiques dans les lignes, les colonnes et les deux diagonales centrales. Les Constantes magiques sont toutes différentes.
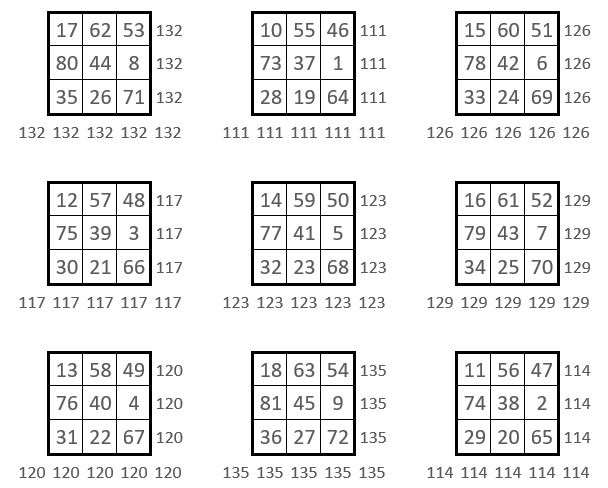
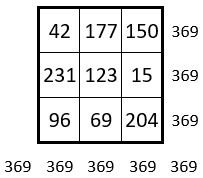
Ces Constantes magiques forment un carré magique ( Ci-contre ) lui-même de Constante magique M’3 = 369, la même que celle du carré magique initial.
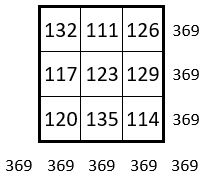
Les sommes des termes dans chacun de ces 9 carrés magiques d’ordre n = 3, forment elles-mêmes également un carré magique, non normal, de Constante magique M’3 = 369 ( Ci-contre ) On remarque que ces deux carrés magiques sont identiques.
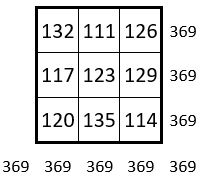
Et voici le carré magique correspondant d’ordre n = 9, issu du pavage des 9 sous-carrés d’ordre n = 3 ci-dessus, de Constante magique M9 = 369 :
On peut alors poursuivre la manip, en sélectionnant à nouveau les termes homologues des sous-carrés d’ordre n = 3 du carré magique d’ordre n = 9 ci-dessus, pour construire encore 9 carrés magiques d’ordre n = 3 :
Les 9 Constantes magiques des 9 carrés magiques obtenus dans cette manip, forment un carré magique ( Ci-contre ) lui-même de Constante magique M’3 = 369, la même que celle du carré magique initial. Ce carré magique est cependant différent de celui obtenu dans la manip qui précède.
On constate à nouveau que les sommes des termes dans chacun de ces 9 carrés magiques d’ordre n = 3, forment elles-mêmes un carré magique, non normal, de Constante magique M’3 = 1 107 ( Ci-contre ) On remarque que l’on obtient le même carré magique d’ordre n = 3, que celui obtenu dans la manip qui précède.
Et voici le carré magique correspondant d’ordre n = 9, composé du pavage des 9 cous-carrés d’ordre n = 3 ci-dessus, de Constante magique M9 = 369 :
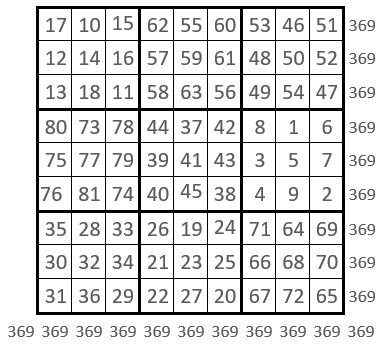
Rien n’empêche, semble-t-il, de poursuivre l’expérience . . . jusqu’où ? Peut-on augurer que l’on retombe sur la même série de 9 sous-carrés magiques d’ordre n = 3, ainsi que sur le même carré magique d’ordre n = 9 initial, au terme de la 9ème manip, et que le cycle est alors bouclé ?
Dénombrement
Les carrés magiques d’ordre n = 3, A et B, qui sont associés en première ligne, appartiennent à la même série des 8 formes du Lo Shu.
On assiste alors à une combinaison de 8 termes pris 2 à 2 : = 28, ce qui donne le nombre de solutions en application de cette construction, pour n = 9.
La méthode est applicable pour tout ordre « n » carré : 9, 16, 25, 36 . . . avec des propriétés analogues.