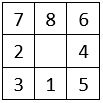
Je nomme « Carrés multiples », une grille numérique carrée d’ordre « n », remplie avec les n2 premiers entiers, dont tous les alignements de n chiffres, quel que soit le sens de lecture, forment des nombres multiples d’un nombre donné.
Sommaire
Les carrés multiples de 3 : Le Lo Shu
Le bon exemple est donné par les huit formes du Lo Shu, formés avec les chiffres depuis 1 jusqu’à 9 :
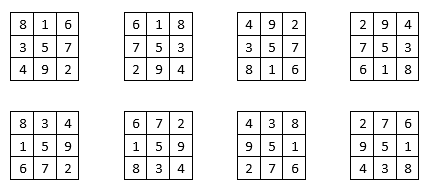
Tous les nombres formés par les alignements de 3 chiffres, quel que soit le sens de lecture, sont des multiples de 3.
On dénombre huit alignements par grille, pouvant se lire dans les deux sens, soit 16 nombres possibles par grille, et au total : 8 x 16 = 128 nombres pour les huit grilles.
En réalité, parmi ces 128 nombres, il n’y a que 16 nombres différents, tous contenus dans l’une quelconque des grilles, après élimination des nombres qui font double emploi. On a affaire à des arrangements de m objets pris p à p, sans doublets ou triplets, dont le dénombrement total est donné par la relation :
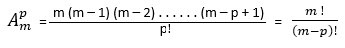
Avec : m = 9 et p = 3, on obtient ainsi au total :

Rappelons que par arrangements de m objets pris p à p, on entend l’ensemble des groupes de p objets pris parmi les m objets de la collection, chaque groupe étant différent des autres par la nature des objets du groupe ou par l’ordre de leur placement dans le groupe.
On se trouve ainsi disposer d’une collection de 504 groupes de 3 chiffres, tous différents, que l’on se propose de regrouper 3 par 3 dans une grille de 9 cases : le nombre de ces regroupements ou arrangements, qui correspondent au nombre de grilles de 9 cases, nous est donné par la relation ci-dessus, avec m = 504 et p = 3 :
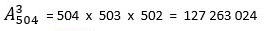
On a donc plus de 127 millions de grilles 9 cases formées avec les chiffres depuis 1 jusqu’à 9 de cette façon.
Les carrés multiples de 9
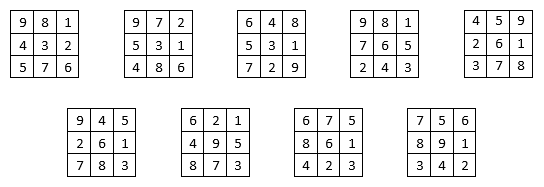
On dénombre neuf solutions de base ( 1 ) : tous les nombres de 3 chiffres, quel que soit le sens de lecture, soit 16 nombres par grille, sont des multiples de 9, et naturellement des multiples de 3.
Si l’on tient compte des 8 formes classiques que peut prendre tout carré numérique par symétries et rotations, on obtient ainsi : 8 x 9 = 72 solutions au total, dans lesquelles on dénombre :
72 x 16 = 1 152 nombres de 3 chiffres multiples de 9, mais qui ne sont pas tous différents.
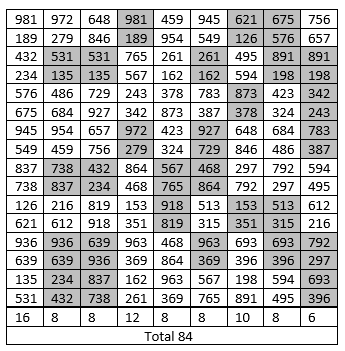
Après élimination des nombres qui font double emploi au moyen du crible ci-dessous, il n’y a pas d’autre moyen, il reste 84 nombres différents.
Il n’y aurait pas de possibilité de construire des Carrés multiples d’ordre pair, ni des carrés multiples d’ordre n = 5 (Henri Camons )
Des carrés multiples à trou central
Henri Berna ( 2 ) propose un Carré multiple de 3 à trou central : voici sa solution, avec les huit premiers entiers : tous les nombres de 3 chiffres, quel que soit le sens de lecture, sont des multiples de 3.
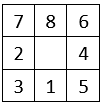
Combien de grilles de ce genre peut-on construire avec les huit premiers entiers ?
Dans ce cas, on a affaire à une permutation circulaire de m = 8 objets.
Le nombre de permutations circulaires est donné par la relation : PCm = ( m – 1 ) !
Avec m = 8 , on a : PC8 = ( 8 – 1 ) ! = 7 ! = 5 040.
La solution de Henri Berna est-elle unique ?
Autre exemple : un carré multiple à trou central de 9.
On n’a pas à chercher bien loin : il y a trois solutions parmi les 9 solutions de base du problème qui précède :
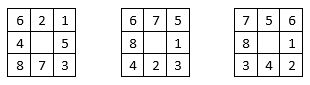
Il suffit d’éliminer le chiffre « 9 » qui se trouve dans la case centrale des trois dernières grilles parmi les neuf de la page qui précède.
On a le même dénombrement que ci-dessus.
Y a-t-il d’autres solutions ?
( 1 ) Henri Camons – Un carré de neuf – Tangente, n° 6, Août-Septembre 1988, pp. 20-21
( 2 ) Henri Berna – Cryptarismes, graphes et autres énigmes mathématiques – Vuibert, 1999, 143pp – pp. 22 et 139.