John Horton Conway ( 1937 – 2020 ) est un mathématicien britannique, bien connu en particulier, comme inventeur du Jeu de la Vie, entre autres.
Dans la méthode de construction des carrés magiques normaux d’ordre impair, n=2 k + 1, mise au point par J. H. Conway, les nombres impairs et les nombres pairs sont géométriquement séparés.
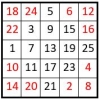
Exemple pour un carré d’ordre n=5
On place les nombres impairs de la suite des n2 = 25 premiers entiers dans le losange central de la grille d’ordre n = 5, de 25 cases, comme il est indiqué dans la figure de gauche ci-dessus. Ces nombres sont à leur place définitive dans le carré magique potentiel.
On considère alors les diagonales brisées montantes de n = 5 nombres impairs, issues du losange central, que l’on complète successivement par les nombres pairs qui leur font défaut dans la suite naturelle.
Dans la première diagonale « 1, 3, 5 », les nombres pairs « 2 et 4 » font défaut : on les place dans cet ordre-là, à la suite dans cette diagonale brisée ( nombres en rouge ).
Dans la seconde diagonale « 7, 9 », il manque les nombres pairs « 6, 8 et 10 », que l’on place dans cet ordre-là, à la suite dans cette diagonale brisée.
Et ainsi de suite. On obtient un carré magique normal d’ordre n = 5, de Constante magique M5 = 65. Et c’est un carré magique de type associé, de Constante de polarisation P5 = n2 + 1 = 26.
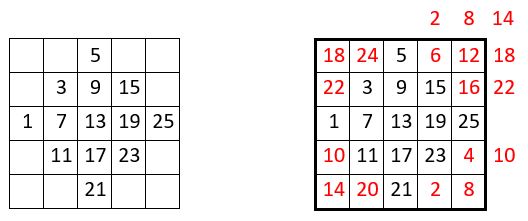
Exemple pour un carré d’ordre n=7
On obtient un carré magique normal de type associé, d’ordre n = 7, de Constante magique M7 = 175,
et de Constante de polarisation
P7 = n2 + 1 = 50.
On peut toujours remplir le losange central de 8 façons différentes ; on obtient ainsi 8 solutions pour le carré magique en construction.
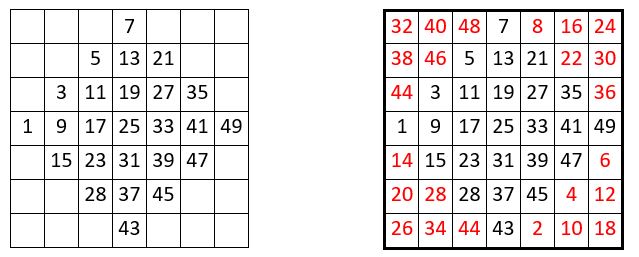
Exemple pour un carré d’ordre n=3
Et bien sûr la Méthode Conway est applicable à l’ordre n = 3
On peut remplir le losange central de 8 façons différentes ; ce qui conduit aux 8 formes du Lo Shu.
La Méthode du Losange de Harry A. Sayles
Voici une méthode originale pour construire un carré magique ayant la même propriété que le carré magique d’ordre impair construit par la Méthode Conway, c’est-à-dire dans lequel les nombres impairs sont concentrés dans le losange central. Cette méthode est aussi appelée Méthode du Losange.
Cette méthode est basée sur deux carrés latins auxiliaires de même ordre.
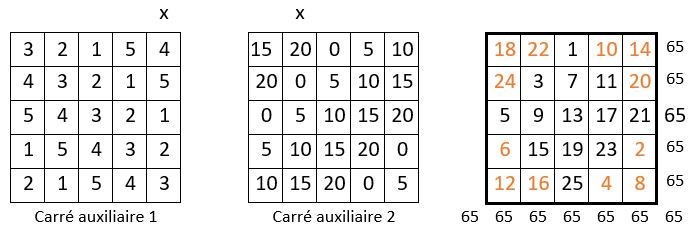
▶ On place dans la première ligne du carré auxiliaire 1, les termes de la série « 1, 2, 3, 4, 5 » dans leur ordre naturel, vers la droite ou vers la gauche, à partir de la case centrale de cette première ligne.
▶ Dans le carré auxiliaire 2, on place les termes de la série « 0, 5, 10, 15, 20 », dans cet ordre, à partir de la case centrale, de façon symétrique par rapport au placement des termes correspondants dans le carré auxiliaire 1.
▶ On ordonne toujours ces carrés latins :
– Sur la dernière colonne dans le carré auxiliaire 1
– Sur la seconde colonne dans le carré auxiliaire 2.
▶ On additionne les cases homologues des deux carrés auxiliaires. On obtient un carré magique d’ordre n = 5, de Constante magique M5 = 65, et c’est un carré magique de type associé, de Constante de polarisation P5 = n2 + 1 = 26.
Tous les nombres impairs sont bien concentrés dans le losange central.
Le placement des termes de la première série des cinq premiers entiers consécutifs, dans la première ligne du carré auxiliaire 1, peut débuter dans une case quelconque de cette ligne ; mais alors on n’obtient pas toujours un carré magique, mais un carré semi-magique.
Il y a « 2n » placements possibles des termes de la première série dans le carré auxiliaire 1, qui conditionne le placement des termes de la seconde série dans le carré auxiliaire 2, pour chaque nombre impair, donc « 2n » solutions pour le carré magique.
La méthode s’applique, mutatis mutandis, aux ordres impairs.
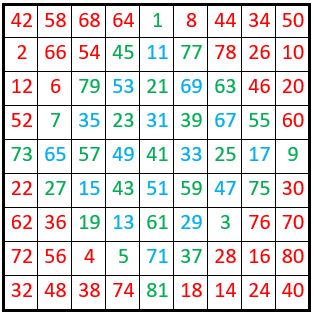
Un carré magique rare et remarquable de L. S. Frierson
C’est un carré magique de type associé, d’ordre n = 9, de Constante magique M9 = 369,
et de Constante de polarisation P9 = n2 + 1 = 82.
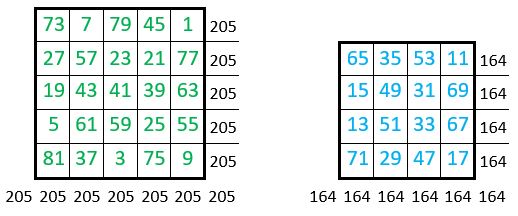
On trouve dans le losange central, aux lignes impaires, un carré magique, d’ordre n = 5, de Constante magique M’5 = 205 ; et c’est un carré magique de type associé, de Constante de polarisation P5 = 82.
Le carré intérieur, aux lignes paires, d’ordre n = 4, est également magique, de Constante magique M’4 = 164.
L’idée vient d’assembler les groupes de dix nombres situés aux sommets du carré magique d’ordre n = 9, pour former une figure en losange.
Les couples symétriques par rapport au centre de ce losange, dits complémentaires, ont même somme, S = 82, une propriété léguée par le carré magique formateur d’ordre n = 9, lui-même de type associé.
▶ John Horton – Conway Wikipedia
▶ L. S. Frierson – A mathematical study of magic squares; The Monist,1907, vol 17
▶ Lucien Gérardin, Les carrés magiques, Editions Dangles, 1986