Sur cette page sont proposés des études, jeux, programmes… concernant les carrés magiques, écrits et réalisés par les lecteurs de ce blog. Si vous souhaitez également partager une de vos réalisations, contactez-nous !
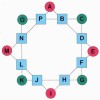
Clifford W. ADAMS , après 47 ans de recherches acharnées résolut enfin en 1957 l’Hexagone Magique à 19 alvéoles proposé par William RADCLIFFE en 1910.
Arsène Durupt, qui a dépassé l’âge de 90 ans s’est intéressé à cet hexagone : »Je me suis penché sur ce problème et, avec la LOGIQUE seulement, je l’ai résolu en 48 heures ! »
Le carré SATOR (ou ROTAS) est une grille carrée de cinq de côté. Cinq est le Nombre constructeur issu de la Division Primordiale (le Nombre d’Or). (le pentagone, base du dodécaèdre dont Dieu se servi pour faire le Tout, selon Platon). Les cinq doigts de la main, avec lesquels l’homme construit. La croix decrite dans le document est la « clé » permettant « d’ouvrir » le SATOR.
Ce qui m’intéresse, devant un carré magique, est de tenter d’en comprendre la logique. Cela m’a amené, également, à rechercher ce qui, dans ce cadre, peut réunir, ce qui distingue ou sépare les différentes sortes de carrés ( premiers, non premiers; et alors impairs ou pairs; puis pairement ou impairement pairs). Ainsi j’ai cherché à mettre au point une méthode de construction simple, LOGIQUE, et adaptable aux différents carrés. Celle que j’ai définie ne concerne pas, toutefois, les impairement pairs, mais j’en donne la raison. Je propose, également, quelques pistes de réflexion. N’étant pas mathématicien, je ne peux les explorer plus avant. J’espère que l’on pourra m’aider à répondre aux questions qui se posent alors…ou à en découvrir d’autres.
Il était une fois, à LAS VEGAS, un riche Hôtelier qui s’était fait construire un Bel Hôtel de 10.000 chambres luxueuses ainsi qu’un superbe CASINO…
Associant logique et perspicacité, cet agréable divertissement est conçu sur le même principe que celui des mots croisés ….sauf que les lettres sont remplacées par des chiffres et les définitions par de simples opérations ( additions ou multiplications). Ces grilles sont accessibles à tous, puisque basées sur les règles les plus élémentaires de l’arithmétique. De plus, ce jeu repose sur un principe essentiel : Chaque grille doit être résolue sans calculatrice.
Avec ce concept de logique arithmétique, on se rend compte que ce simple divertissement se révèle être un outil pédagogique et ludique très intéressant pour améliorer nos capacités de calcul mental, de logique et surtout de perspicacité.
Les grilles de Jacky Bonnet sont régulièrement publiées dans ‘Science et Vie Junior’, les publications Keesing, ‘La Montagne’, ‘Centre France’ … Jacky Bonnet est également inventeur du jeu de stratégie TOPQUARK.
A 83 ans, Arsène Durupt, lecteur de Sciences et Avenir résidant en Côte d’Or, a également réalisé, sans l’aide d’un ordinateur, cet objet mathématique : un cube semi-magique, résultat de l’empilement de huit carrés semi-magiques. « Semi-magique » car si la somme des lignes, comme celle des colonnes, est identique, égale à 2052, la somme de deux diagonales ne l’est pas et vaut exactement le double, soit 4104. En outre, la même propriété s’applique dans la verticalité entre les tranches empilées. (SCIENCES ET AVENIR – MARS 2006 – 21)
Cette méthode qui s’applique aux carrés magiques d’ordre impair, est expliquée pas à pas, avec exemples d’application pour l’ordre n = 9, accompagnée par un Commentaire de René Descombes.
Page personnelle: Eric Sizaret
1ere étude: Carré magique d’ordre impair:
On arrive à résoudre les carrés magiques plus ou moins facilement en utilisant généralement un carré préliminaire qui se remplit de différentes façons suivant les auteurs qui se sont penchés sur la question. On passe ensuite à l’exécution du carré définitif par différentes méthodes dont nous exposerons ci-après celle développée et mise au point par l’auteur de ce mémoire, dite méthode COUTURIER pour ce qui concerne les carrés magiques de type impair et ceci sans aucun calcul , et sans limitation du nombre de cases par côté.
2eme étude: Carré magique d’ordre pair:
Si on compare les carrés magiques de type impair à ceux de type pair, on s’aperçoit qu’il existe des différences notables qui font que : Le plus petit carré de type pair est d’ordre 4, soit 4 cases par côté. La méthode COUTURIER pour les carrés magiques de type impair exposée dans la première étude n’est pas applicable pour les carrés de ce type. En effet les carrés de type pair n’ont plus de case centrale ce qui fait que la somme magique ne peut plus s’exprimer par S = NC x N ( avec NC nombre de la case centrale et N nombre de cases par côté), ; et de ce fait leur résolution est loin d’être aussi simple.
3eme étude : Les carrés magiques gigognes:
Ce sont des carrés magiques de type impair ou pair qui ont comme particularité de contenir un ou plusieurs autres carrés magiques eux aussi. Certains auteurs les appellent aussi carrés magiques à enceintes ou multimagiques. Pour imager cette définition, on pourrait dire qu’ils s’emboîtent comme des poupées russes.
4eme étude : Les carrés magiques pairs et impairs:
La différence avec ce que j’ai écrit précédemment est que je pars d’une somme magique que je me fixe pour déterminer le carré magique correspondant à cette somme.
5eme, 6eme et 7eme étude : Les carrés magiques mosaïques:
Les « carrés magiques mosaïques » sont des carrés magiques qui contiennent d’autres carrés magiques assemblés par juxtaposition comme un dallage à l’intérieur de ceux-ci ; certains les nomment « carrés à compartiments ».