Les carrés magiques répétitifs

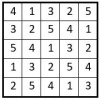
Dans un carré magique normal d’ordre n, la suite des n² premiers entiers est utilisée une seule fois.

Lorsque l’on utilise plusieurs fois une suite des premiers entiers pour obtenir la magie dans les lignes, les colonnes et les deux diagonales centrales, on qualifie ce carré magique de carré magique répétitif normal.

Cette catégorie de carrés magiques, est absente dans la plupart des traités consacrés aux carrés magiques,  ou dans les chapitres intéressant les carrés magiques dans les ouvrages de récréations mathématiques.

Dans les carrés magiques ou semi-magiques répétitifs, on n’observe pas, stricto sensu, la définition classique des carrés magiques ; d’où cette exclusion des traités des carrés magiques.

Cependant, ces carrés magiques ou semi-magiques répétitifs ne manquent pas d’intérêt. Il existe de nombreuses méthodes de construction de ces carrés magiques ou semi-magiques répétitifs, qui présentent nombre de propriétés propres.

1 La magie primaire. Rappel.
2 Les carrés magiques répétitifs. Définition.
3 Les carrés (semi) magiques répétitifs
    3.1 Le carré latin : un carré (semi) magique répétitif.
    3.2 Le Sudoku : un carré (semi) magique répétitif.
4 Quelques méthodes de Construction
    4.1 La méthode de Construction la plus simple : le Lo Shu catalyseur.
    4.2 Une méthode de construction générale.
    4.3 Une autre méthode de construction avec catalyseur
    4.4 Méthodes de construction avec le carré naturel alterné
5 Construction d’un carré magique répétitif d’ordre n = 9
    5.1 Première Méthode de construction
    5.2 Variante de la méthode de construction du carré d’ordre n=9
    5.3 Autre Variante de construction du carré d’ordre n = 9
    5.4 Exemples de carrés magiques répétitifs d’ordre n = 9, de même Constante magique

1 Construction d’un carré magique répétitif d’ordre n = 8
    1.1 Le carré magique normal d’ordre n = 4 est le catalyseur
    1.2 Un carré semi-magique répétitif d’ordre n = 8
    1.3 Une seconde application de la méthode
    1.4 Une troisième application de la méthode
    1.5 Un exemple de carré magique répétitif d‘ordre n = 8
    1.6 Un autre exemple de carré magique répétitif d‘ordre n = 8
    1.7 Deux carrés semi-magiques répétitifs d’ordre n = 8, de formation ou d’origine différente.
    1.8 Un carré semi-magique répétitif d’ordre n = 8.
    1.9 Un carré magique répétitif d’ordre n = 8 à quartiers égaux.
    1.10 Un carré semi-magique répétitif mystérieux d’ordre n = 8 .
2 Construction d’un carré magique répétitif d’ordre n = 10
3 Construction d’un carré magique répétitif d’ordre n = 12

1 Construction d’un carré magique répétitif d’ordre n=16
    1.1 Un beau carré magique répétitif d’ordre n = 16
    1.2 Exemple de carré semi-magique répétitif d’ordre n = 16
    1.3 Autre structure de carré semi-magique répétitif d’ordre n = 16
    1.4 Une construction du carré magique répétitif d’ordre n = 16
    1.5 Le pavé d’assemblage dans tous ses états.
    1.6 Une variante des quatre carrés formateurs
2 Le carré naturel formateur

1 Construction d’un carré magique répétitif d’ordre n=6
    1.1 Une méthode de construction prolifique
    1.2 Un carré semi-magique répétitif d’ordre n = 6
    1.3 Une panoplie de la grille d’ordre n = 6
2 Le carré magique répétitif d’ordre n = 3
    2.1 Le carré magique répétitif non normal
    2.2 Le carré magique répétitif d’ordre n = 3. Une panoplie.
3 Un carré magique normal d’ordre impair
    3.1 Application pour n=5
    3.2 Application pour n=9
4 Un carré magique répétitif d’ordre pair
    4.1 Application pour n=4
    4.2 Application pour n=6
5 Les rectangles magiques répétitifs
6 Un carré magique répétitif issu du cube magique.