Introduction Partie 1 Partie 2 Partie 3 Partie 4
Sommaire
La magie primaire. Rappel.
Le carré magique normal ou primaire classique utilise une seule fois la suite des n2 premiers entiers pour obtenir la magie des lignes, des colonnes et des deux diagonales centrales. Exemples pour n = 4 :
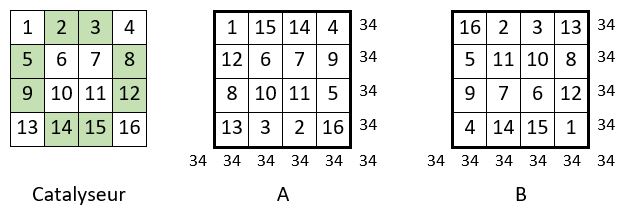
Première méthode de construction. On sélectionne les termes de la couronne périphérique dans le carré naturel d’ordre n = 4, choisi comme catalyseur. Dans cette couronne, on permute les couples opposés par le centre de la grille. Les autres termes restent à leur place. La Grille « A » est un carré magique normal, de Constante magique M4 =34.
Seconde méthode de construction avec le même catalyseur. On considère les termes sélectionnés de la couronne périphérique du catalyseur à leur place définitive. On permute les autres couples. La Grille « B » est un carré magique normal, de Constante magique M4 = 34.
Il y a de nombreuses méthodes de construction des carrés magiques normaux. Le carré naturel normal ou alterné, joue souvent le rôle de catalyseur.
Les carrés magiques répétitifs. Définition.
Lorsque l’on utilise plusieurs fois une suite ou une série de termes pris parmi les n2 premiers entiers pour obtenir la magie dans les lignes, les colonnes et les deux diagonales centrales, on a affaire à un « carré magique répétitif » ou un « carré magique à répétition » normal.
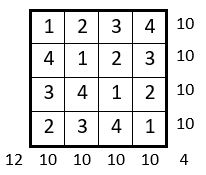
Voici à titre d’exemple, un carré semi-magique répétitif normal, d’ordre n = 4, et de Constante magique M’4 = 10 ; les diagonales centrales ne sont pas magiques.
La suite des n2 = 4 premiers entiers est répétée 4 fois. Les termes homologues sont situés sur une permutation figurée.
Encore faut-il préciser ce l’on entend par « répétition ».
Prenons l’exemple de la grille d’ordre n = 6 de 36 cases. On peut concevoir théoriquement un carré magique ou semi-magique répétitif dans lequel :
a – Les 18 premiers entiers répétés deux fois ;
b – Les deux premiers entiers répétés dix-huit fois ;
c – Les 12 premiers entiers répétés trois fois ;
d -Les trois premiers entiers répétés douze fois ;
e – Les 9 premiers entiers répétés quatre fois ;
f – Les 4 premiers entiers répétés neuf fois ;
g- Et enfin les six premiers entiers répétés six fois.
Il y a donc sept options théoriques, pour la grille d’ordre n = 6. On peut alors se poser la question : « Est-ce possible ? Peut-on réaliser au moins un carré magique ou semi-magique dans chacune de ces options ? »
Le seul moyen de répondre à cette question, est de tester chacune de ces options. ( Voir le n° 32 )
Voici quelques exemples :
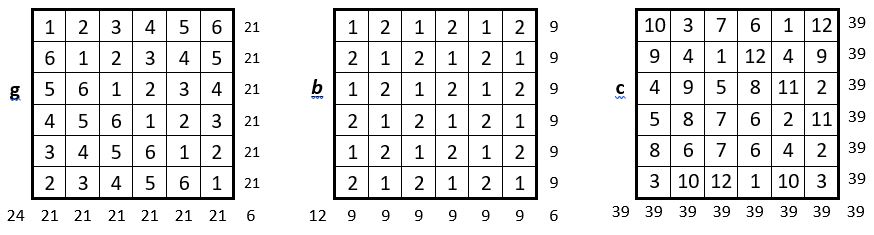
Chaque grille carrée peut être testée de la même façon. Certaines grilles, celles dont l’ordre est un nombre premier, n’ont qu’une option : ainsi la grille d’ordre n = 7 de 49 cases : les sept premiers entiers répétés sept fois, seule option.
Les carrés (semi) magiques répétitifs
Le carré latin : un carré (semi) magique répétitif.
Tout carré latin numérique peut être considéré comme un carré (semi) magique répétitif.
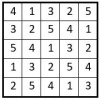
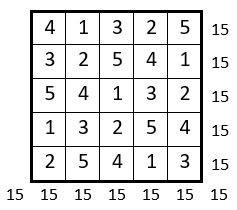
Voici ci-contre un carré latin d’ordre n = 5 : on trouve dans les lignes et les colonnes la suite des cinq premiers entiers.
Cela correspond exactement à la définition du carré magique ou semi-magique répétitif énoncée ci-dessus. De plus, le carré latin ci-contre est diagonal : c’est un carré magique répétitif.
Le Sudoku : un carré (semi) magique répétitif.
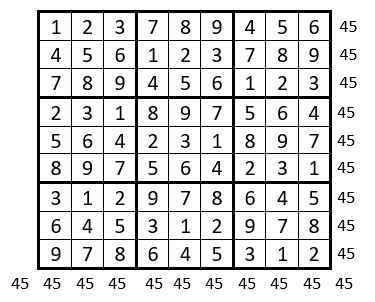
Rappelons que le Sudoku classique est un carré latin d’ordre n = 9, dont les lignes et les colonnes sont constituées par la suite des neuf premiers entiers, avec une contrainte complémentaire : cette suite des neuf premiers entiers doit figurer dans chacun des neuf sous-carrés de 9 cases.
En sa qualité de carré latin, le Sudoku peut ainsi être considéré comme un carré magique répétitif normal.
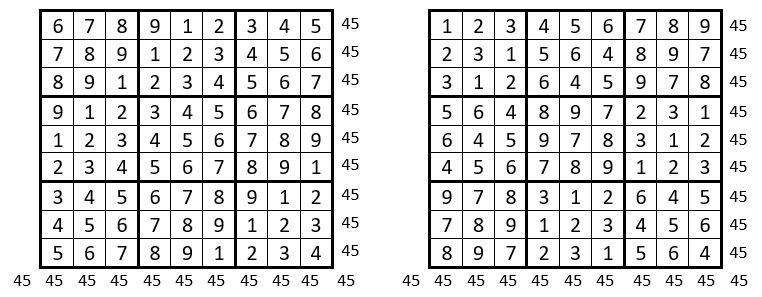
Le Sudoku ci-contre, est un Sudoku diagonal : c’est donc un carré magique répétitif, d’ordre n = 9, de Constante magique M’9 = 45.
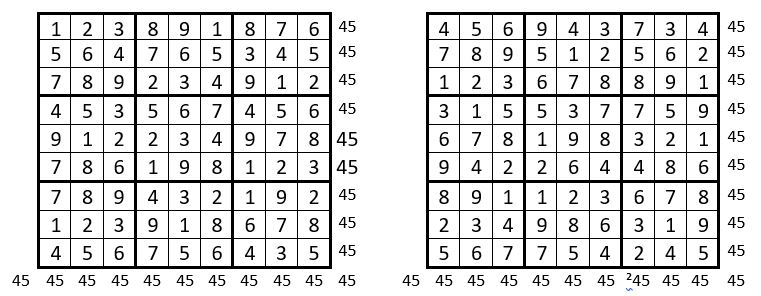
Voici encore un exemple de Supersudoku diagonal d’ordre n = 16, considéré comme un carré magique répétitif normal de même ordre, et de Constante magique M’16 = 136 :
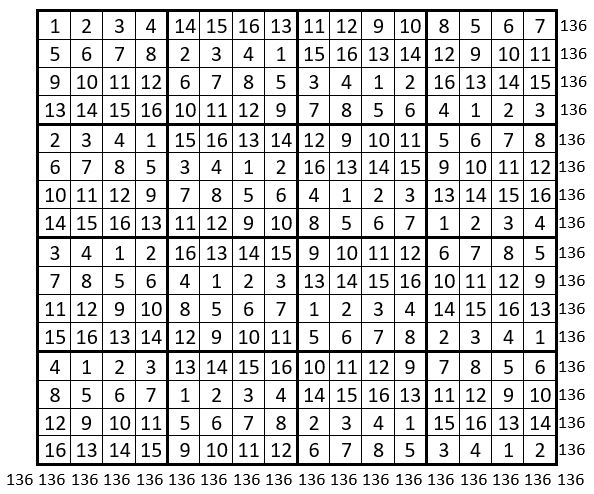
Cette catégorie de carrés magiques, les carrés magiques répétitifs, est absente dans la plupart des traités intéressant les carrés magiques, ou dans les chapitres consacrés aux carrés magiques dans les ouvrages de récréations mathématiques.
Dans les carrés magiques ou semi-magiques répétitifs, on n’observe pas, stricto sensu, la définition classique des carrés magiques ; d’où leur exclusion des traités des carrés magiques . . .
Cependant ces carrés magiques ou semi-magiques répétitifs ne manquent pas d’intérêt. Il existe de nombreuses méthodes de construction de ces carrés magiques ou semi-magiques répétitifs, qui présentent de nombreuses propriétés propres.
Quelques méthodes de Construction
La méthode de Construction la plus simple : le Lo Shu catalyseur.
On place l’une ou l’autre des huit formes du Lo Shu, dans les 9 sous-carrés de 9 cases de la grille d’ordre n = 9 préparée à cet effet. On obtient un carré magique répétitif normal élémentaire d’ordre n = 9, de Constante magique M’9 = 45
Ce carré magique répétitif normal utilise 9 fois les 9 premiers entiers.
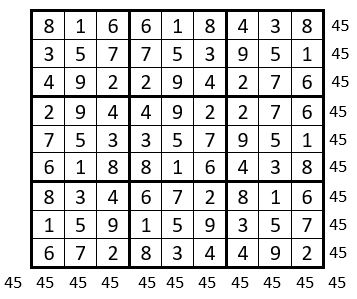
Les termes de chacun des 9 sous-carrés de 9 cases, ont même somme : S = 45, par construction.
Dans le cadre des placements du catalyseur, on dénombre au moins : N = 9 ! = 362 880 solutions.
On peut choisir comme catalyseur tout carré magique normal, et le nombre n2 de répétitions est aussi quelconque.
Une méthode de construction générale.
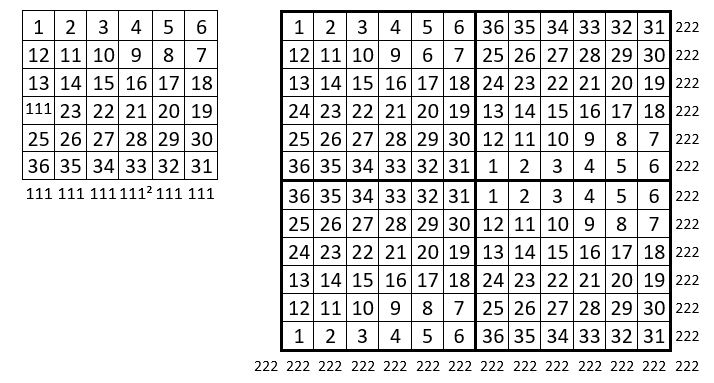
Cette méthode utilise le carré naturel alterné d’ordre n = 6, choisi comme catalyseur.
On place tout d’abord, en diagonal, dans les quartiers opposés 1 et 3 d’une grille d’ordre n = 12, le carré naturel alterné d’ordre pair, n = 6, tel quel.
On place ensuite le symétrique de chacune de ces grilles par rapport à la médiane horizontale de la grille d’ordre n = 12.
Dans la figure obtenue, les termes des lignes, des colonnes et des diagonales centrales, totalisent tous la somme S = 222 ; ce carré correspond ainsi à la définition du carré magique répétitif normal..
On peut choisir comme catalyseur, un carré magique normal de tout ordre.
Une autre méthode de construction avec catalyseur
Utilisons pour le catalyseur, le carré naturel alterné d’ordre impair, n = 5.
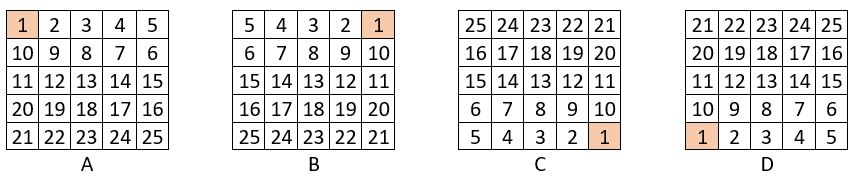
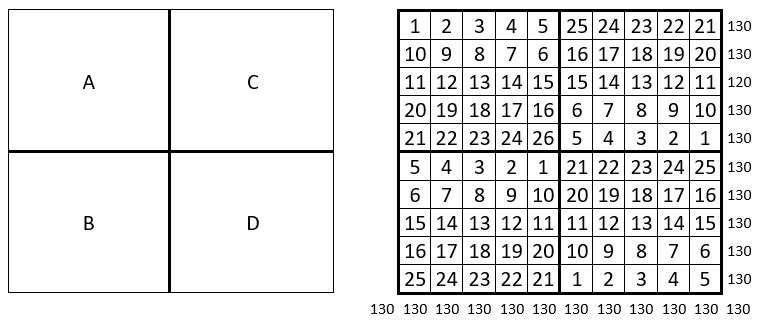
On sélectionne quatre formes du carré naturel alterné d’ordre n = 5 : A, B, C et D, en choisissant pour origines successives les quatre sommets de la grille.
On place ces formes A, B, C et D, dans les quartiers d’une grille d’ordre n = 10, comme il est indiqué dans la grille formatrice de gauche ci-dessus.
Dans la grille obtenue, les termes des lignes, des colonnes et des diagonales centrales, ont même somme, S = 130 : il s’agit bien d’un carré magique répétitif normal d’ordre n = 10.
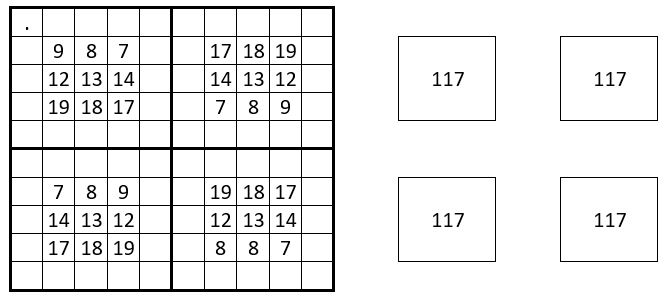
On remarque que les carrés d’ordre n = 3 de 9 cases, situés au centre des quartiers de ce carré magique répétitif d’ordre n=10, ont même somme, S = 117. Mais cela ne semble pas une propriété très caractéristique.
Méthodes de construction avec le carré naturel alterné
Utilisons pour le catalyseur, le carré naturel alterné d’ordre n = 3, de 9 cases
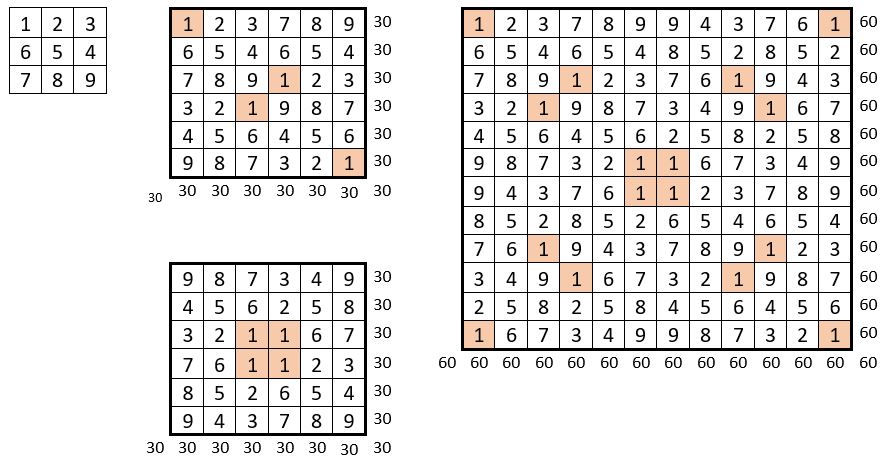
Les deux carrés magiques répétitifs d’ordre n = 6, de 36 cases, utilisent chacun 4 fois les termes du catalyseur d’ordre n=3.
Le carré magique répétitif d’ordre n = 12, de 144 cases, de Constante magique M12 = 60, utilise 16 fois les termes du catalyseur d’ordre n = 3.
Construction d’un carré magique répétitif d’ordre n = 9
Première Méthode de construction
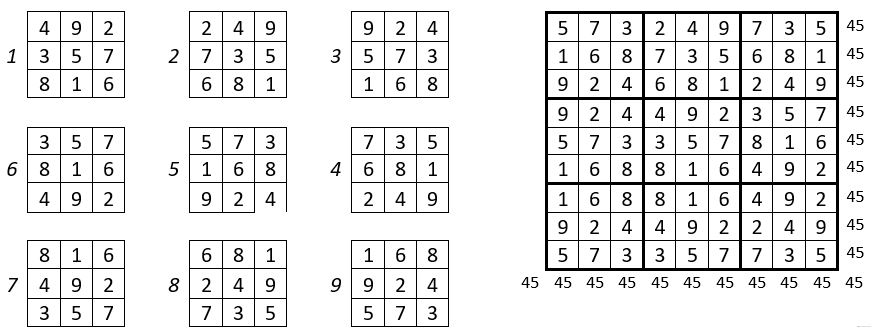
On place 9 formes du catalyseur choisi, qui correspondent à un carré magique ou semi-magique d’ordre n = 3, dans la grille d’ordre n = 9, de 81 cases, compartimentée en 9 sous-carrés de 9 cases, conformément au tableau de placement d’ordre n = 3 ci-contre.
La grille d’ordre n = 9 de 81 cases obtenue, utilise les 9 formes du catalyseur ; c’est ainsi un carré magique répétitif, de Constante magique M’9 = 45.
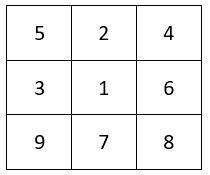
Variante de la méthode de construction du carré d’ordre n=9
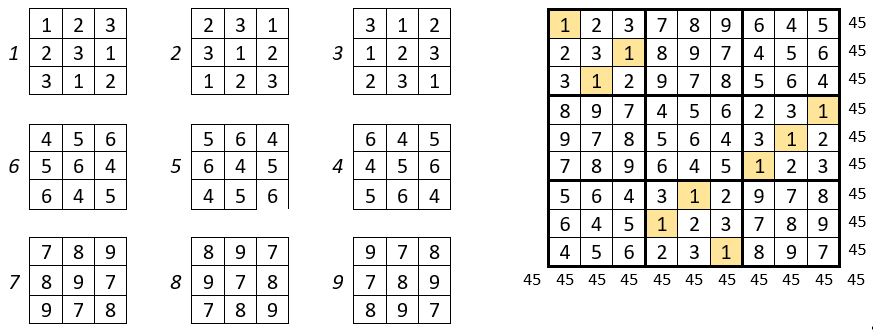
On place les 9 catalyseurs, numérotés depuis 1 jusqu’à 9, conformément au tableau des placements ci-contre.
On obtient un carré magique répétitif d’ordre n = 9, de Constante magique M’9=45. Les termes homologues sont situés sur une permutation figurée.
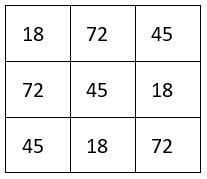
Les sommes des termes des 9 sous-carrés d’ordre n = 3 de 9 cases du carré magique répétitif d’ordre n = 9, forment elles-mêmes un carré magique de Constante magique M’3 = 135 ( ci-contre )
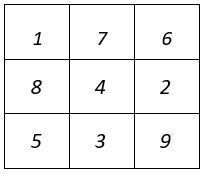
Autre Variante de construction du carré d’ordre n = 9
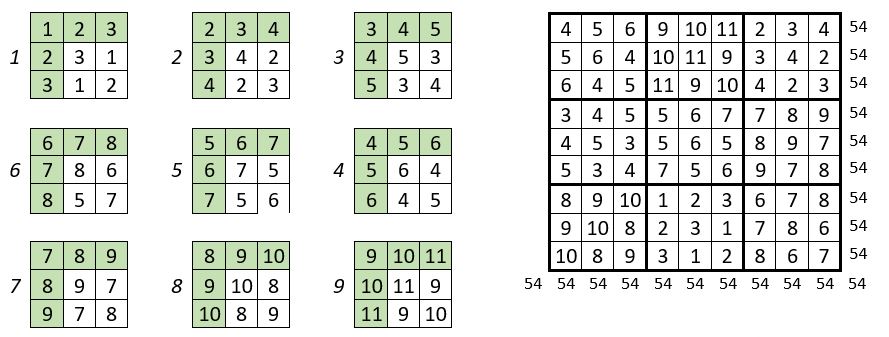
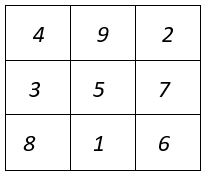
Les carrés formateurs d’ordre n = 3, sont tous construits de la même façon : les termes homologues sont situés sur une permutation figurée. On place ces carrés formateurs numérotés, conformément au pavé d’assemblage ci-contre.
On obtient un carré magique répétitif d’ordre n = 9, et de Constante magique M’9=54.
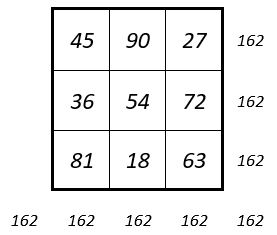
Les sommes des termes des 9 carrés formateurs, forment elles-mêmes un carré magique d’ordre n = 3, et de Constante magique M’3 = 162.
Et c’est un carré magique de type associé, de Somme associative : S = 108 ( ci-contre )
Exemples de carrés magiques répétitifs d’ordre n = 9, de même Constante magique