Introduction Partie 1 Partie 2 Partie 3 Partie 4
Sommaire
- 1 Construction d’un carré magique répétitif d’ordre n = 8
- 1.1 Le carré magique normal d’ordre n = 4 est le catalyseur
- 1.2 Un carré semi-magique répétitif d’ordre n = 8
- 1.3 Une seconde application de la méthode
- 1.4 Une troisième application de la méthode
- 1.5 Un exemple de carré magique répétitif d‘ordre n = 8
- 1.6 Un autre exemple de carré magique répétitif d‘ordre n = 8
- 1.7 Deux carrés semi-magiques répétitifs d’ordre n = 8, de formation ou d’origine différente.
- 1.8 Un carré semi-magique répétitif d’ordre n = 8.
- 1.9 Un carré magique répétitif d’ordre n = 8 à quartiers égaux.
- 1.10 Un carré semi-magique répétitif mystérieux d’ordre n = 8 .
- 2 Construction d’un carré magique répétitif d’ordre n = 10
- 3 Construction d’un carré magique répétitif d’ordre n = 12
Construction d’un carré magique répétitif d’ordre n = 8
Le carré magique normal d’ordre n = 4 est le catalyseur
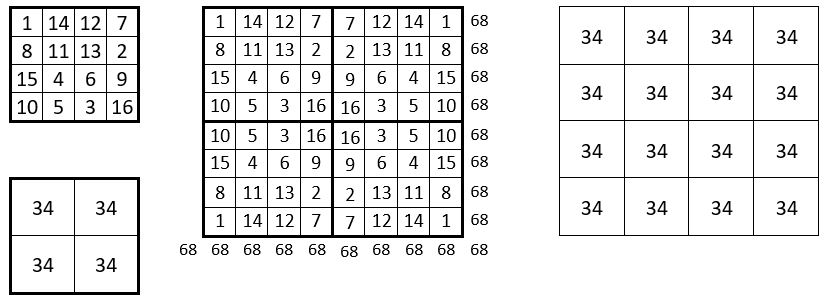
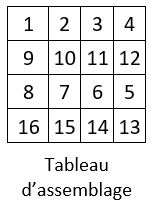
Le carré magique normal d’ordre n = 4, choisi comme catalyseur, est un carré magique normal à quartiers égaux, de somme : S = 34
On place ce carré magique catalyseur dans une grille d’ordre n = 8, de telle manière que chaque terme des lignes et des colonnes soit symétrique par rapport à une médiane horizontale ou verticale de la grille.
La grille d’ordre n = 8 obtenue est un carré magique répétitif de Cte magique M’8 = 68, et c’est un carré magique répétitif à quartiers égaux, de somme S = 136 = 2 x 68.
Le catalyseur est utilisé 4 fois pour obtenir la magie dans le carré magique répétitif.
Les 16 sous-carrés de 4 cases, en damier, ont même somme : S = 34.
On peut choisir comme catalyseur, l’un des 880 carrés magiques normaux de base de la Classification de Frénicle, d’où autant de solutions pour le carré magique répétitif d’ordre n = 8.
Un carré semi-magique répétitif d’ordre n = 8
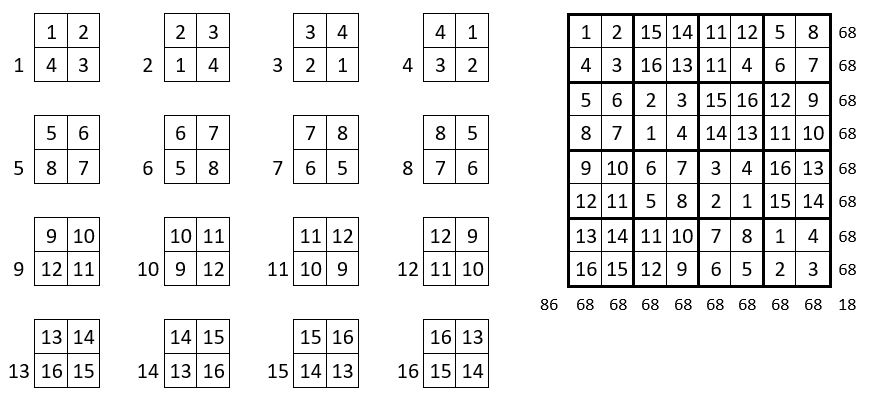
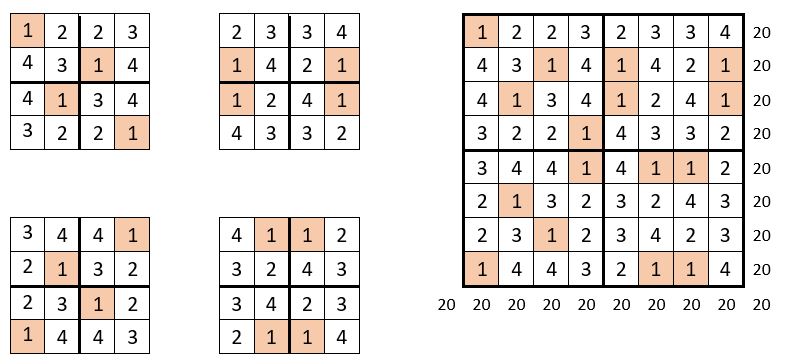
On sélectionne dans la suite des 16 premiers entiers, quatre carrés de 4 cases :
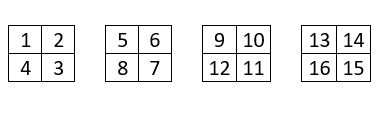
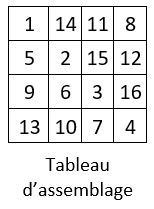
On forme de la même manière en tournant, pas à pas, avec pour origine chacun de ces quatre carrés, quatre suites de carrés de 4 cases, constituant ainsi un tableau de 16 carrés différents de 4 cases, numérotés depuis 1 jusqu’à 16.
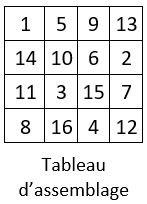
Il s’agit alors de placer ces 16 carrés de 4 cases, dans la grille d’ordre n = 8 préparée à cet effet, pour obtenir la magie dans cette grille. Et c’est un travail de patience, pour établir le tableau d’assemblage correspondant reproduit ci-dessus. Dans ce tableau d’assemblage, les quatre suites consécutives de 4 termes des 16 premiers entiers, sont situées sur une permutation figurée. C’est aussi un carré semi- magique normal d’ordre n = 4, de Constante magique M4 = 34.
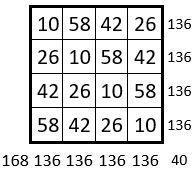
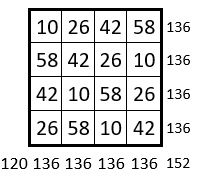
On obtient un carré semi-magique répétitif d’ordre n = 8, de Constante magique M’8 = 68 ; et les sommes des termes des sous-carrés de 4 cases, forment elles-mêmes un carré semi-magique répétitif de Constante magique M’4= 136 : la suite « 10, 26 , 42, 58 » est utilisée quatre fois. Et les termes homologues sont situés sur une permutation figurée ( ci-dessus, à droite )
Ce carré semi-magique répétitif utilise quatre fois la suite des 16 premiers entiers.
II y a peut-être d’autres solutions à rechercher en application de cette méthode, qui reste relativement difficile à première vue ? Cependant, à titre d’essai, on se propose d’utiliser pour résoudre ce problème, la propriété du tableau d’assemblage énoncée précédemment : les quatre sous-séries consécutives de 4 termes des 16 premiers entiers, sont situées sur quatre permutations figurées.
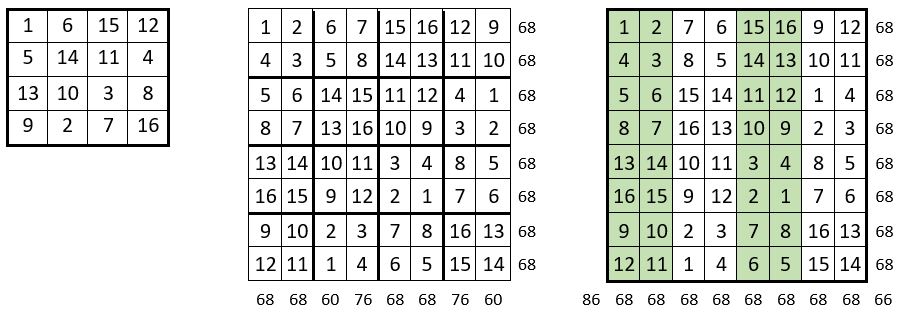
Avec un nouveau tableau d’assemblage, c’est-à-dire un carré semi-magique normal d’ordre n = 4, dans lequel l’on observe la propriété énoncée ci-dessus, on obtient une grille dans laquelle toutes les lignes sont magiques, ainsi que quatre colonnes.
Quatre colonnes restent donc à rendre magiques, par permutations disponibles dans les lignes. Il n’y a que l’embarras du choix. La grille de droite ci-dessus devient semi-magiques après quelques permutations dans les lignes qui s‘y prêtent. Il s’agit bien d’un carré magique répétitif. Il y a ainsi plusieurs solutions, issues du choix des permutations dans les lignes, et du choix du tableau d’assemblage.
Remarque
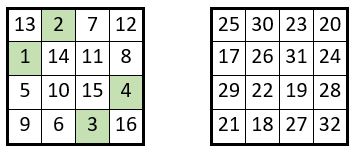
On sait que l’on peut regrouper par quatre les 24 permutations figurées d‘ordre n = 4, dans six grilles d’ordre n = 4. Voici ci-après une solution, les permutations figurées étant présentées sous forme numérique dans les six grilles, avec les 24 sous-séries de 4 termes consécutifs. Il y a d’autres solutions.
Ces six grilles peuvent alors être utilisées comme tableau d’assemblage pour la construction du carré semi-magique répétitif d’ordre n = 8, dans la cadre de la méthode exposée ci-dessus. Il y a donc d’assez nombreuses solutions.
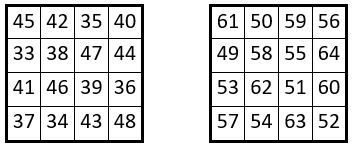
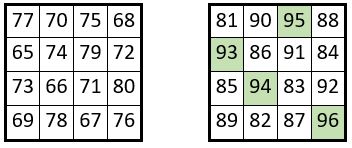
Une seconde application de la méthode
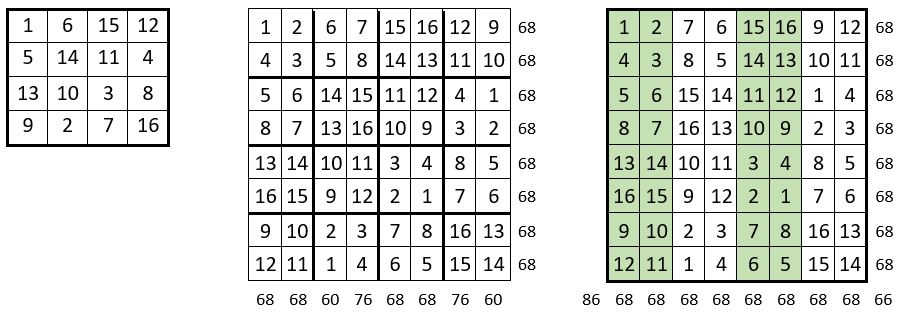
On procède de la même façon que ci-dessus
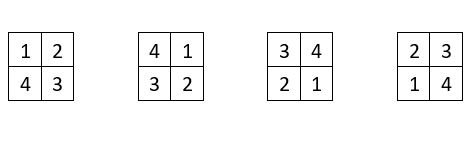
Remarque.
On peut utiliser directement les carrés formateurs classiques de quatre cases.
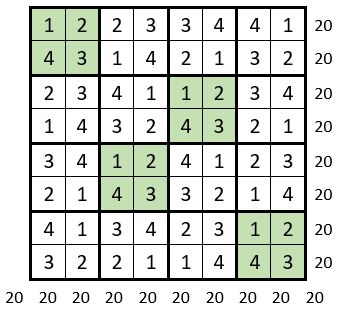
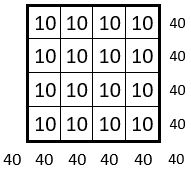
On place ces carrés formateurs sur des permutations figurées dans la grille d’ordre n = 8 de 64 cases. On obtient un carré magique répétitif, d’ordre n = 8 et de Constante magique M’8 = 20.
Il y a de nombreuses solutions, issues du placement des carrés formateurs.
Une troisième application de la méthode
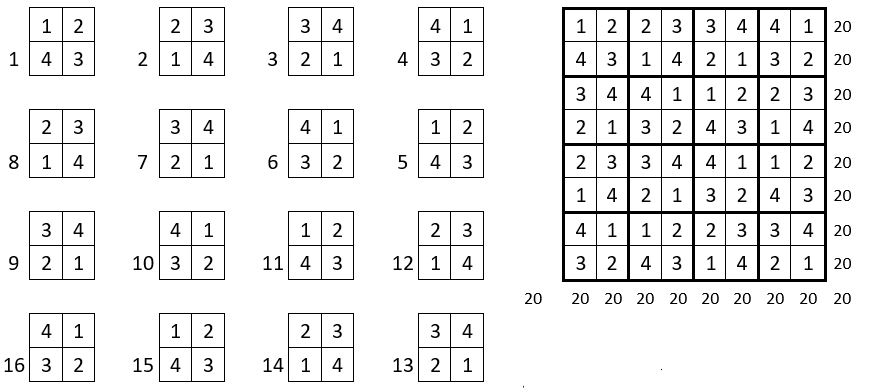
On procède toujours de la même façon que précédemment
Un exemple de carré magique répétitif d‘ordre n = 8
Une proposition de Hannes Bürgel
On utilise 16 fois le carré de base de 4 cases, comportant la première série de 4 termes des premiers entiers ( 1, 2, 3, 4), pour construire les quatre grilles d’ordre n = 4 de 16 cases. On tourne toujours dans le même sens positif, à partir de l’unité située dans une case pochée dans les quatre grilles d’ordre n = 4.
On place alors, dans le même ordre, ces quatre grilles dans la grille d’ordre n = 8 préparée à cet effet.
On obtient un carré magique répétitif d’ordre n = 8, de Constante magique M’8 = 20.
Les termes des 16 sous-carrés de 4 cases, en damier, de ce carré magique répétitif, qui correspondent aux carrés de base de 4 cases, ont tous la même somme : S = 10.
Un autre exemple de carré magique répétitif d‘ordre n = 8
Une proposition de Hannes Bürgel
Les demi-grilles du carré naturel alterné catalyseur d’ordre n=4, sont placées quatre fois dans un ordre approprié, dans la grille d’ordre n = 8 préparée à cet effet.
On obtient un carré magique apprivoisé de Cte magique M’8 = 68. Les dominos de la grille supérieure du catalyseur, ont pour somme S = 9 ; ceux de la grille inférieure ont pour somme constante S = 25.
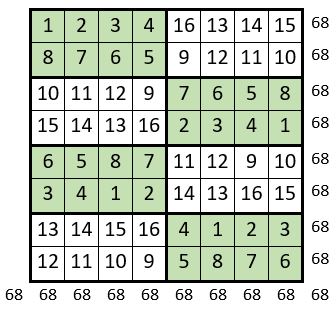
Deux carrés semi-magiques répétitifs d’ordre n = 8, de formation ou d’origine différente.
Une proposition de Hannes Bürgel
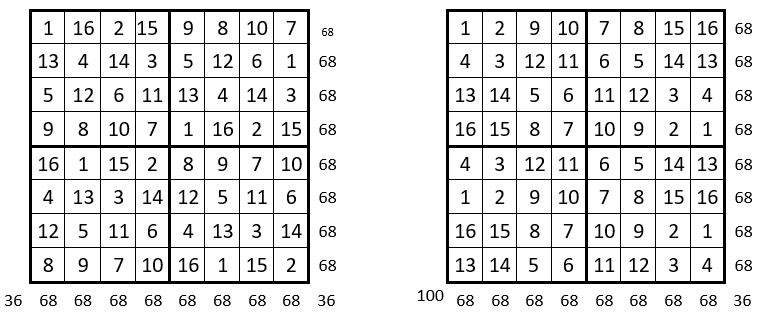
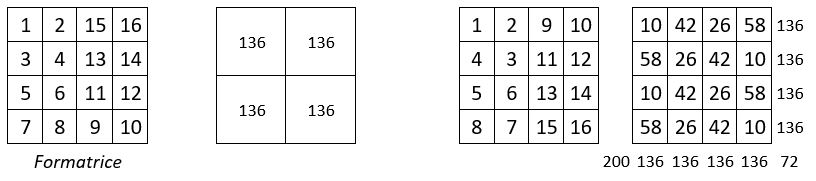
Les lignes de chaque quartier du carré semi-magique répétitif d’ordre n = 8, de gauche, sont formées par les lignes de la Grille formatrice d’ordre n = 4 qui figure au-dessous, utilisées quatre fois. Ce carré semi-magique répétitif, est à quartiers égaux, de somme : S = 136.
Dans le carré semi-magique répétitif de droite, on fait subir un demi-tour vers la droite au premier quartier, que l’on place dans le second quartier, à droite. De même on fait subir un demi-tour vers la droite au troisième quartier, que l’on place dans le quatrième quartier à droite.
On obtient un carré semi-magique répétitif de Constante magique M’8 = 68. Les sommes des 16 sous-carrés de quatre cases, forment eux-mêmes un carré semi-magique, de Constante magique M’4 = 136.
Un carré semi-magique répétitif d’ordre n = 8.
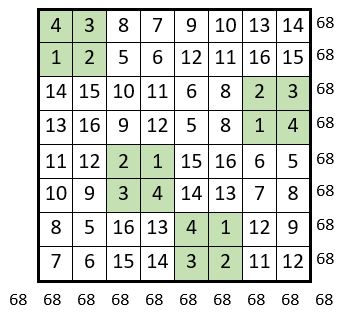
On place chacun des quatre quartiers de la grille naturelle d’ordre n = 4, prise comme catalyseur, dans un ordre approprié, sur une permutation figurée dans la grille d’ordre n=8 de 16 sous-carrés de 4 cases, préparée à cet effet.
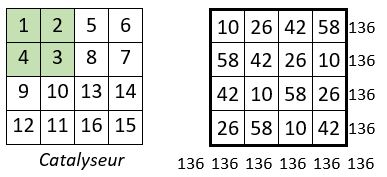
On obtient un carré semi-magique répétitif d’ordre n = 8, de Constante magique M’8 = 68.
Les sommes des termes de chacun des 16 sous-carrés de 4 cases de la grille d’ordre n = 8, forment elles-mêmes un carré magique répétitif de Constante magique M’4 = 136 : la série « 10, 26, 42, 58 » est utilisée quatre fois.
Un carré magique répétitif d’ordre n = 8 à quartiers égaux.
Une proposition de Hannes Bürgel
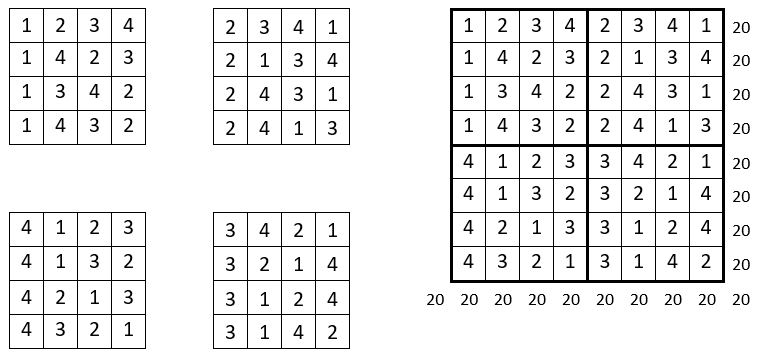
On place les carrés d’ordre n = 4 catalyseurs tels qu’ils se présentent, dans les quartiers de la grille d’ordre n = 8 préparée à cet effet.
On obtient un carré magique répétitif d’ordre n = 8, de Constante magique M’8 = 20 ;
C’est un carré magique répétitif à quartiers égaux, de somme : S = 40.
Les termes des demie-lignes ont tous la même somme : S = 10
Un carré semi-magique répétitif mystérieux d’ordre n = 8 .
Une proposition de Hannes Bürgel
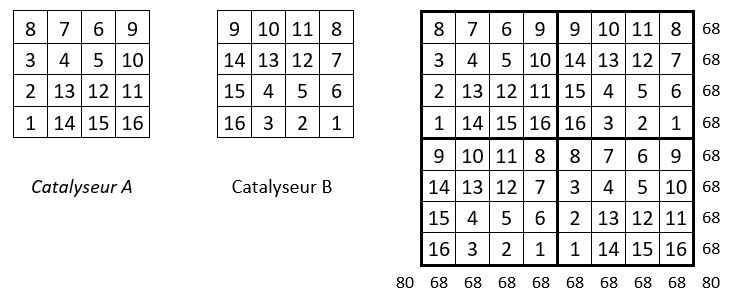
Les deux grilles d’ordre n = 4 présentées ci-dessus, Catalyseur A et Catalyseur B, ont été imaginées par Hannes Bürgel, sans commentaire de ce dernier. Elles contiennent chacune un parcours atypique des 16 premiers nombres entiers, sans que l’on puisse bien déterminer comment, suivant quelle règle éventuelle, ces parcours ont été imaginés par l’auteur. En tous cas, ce ne sont pas des grilles magiques.
On place tels qu’ils se présentent, le Catalyseur A dans les quartiers opposés 1 et 3 d’une grille d’ordre n = 8 de 64 cases ; et le Catalyseur B dans les quartiers opposés 2 et 4 de cette même grille.
On obtient bien un carré semi-magique répétitif, de Constante magique M8 = 68. La méthode de construction de ce carré semi-magique répétitif reste mystérieuse à nos yeux . . .
Construction d’un carré magique répétitif d’ordre n = 10
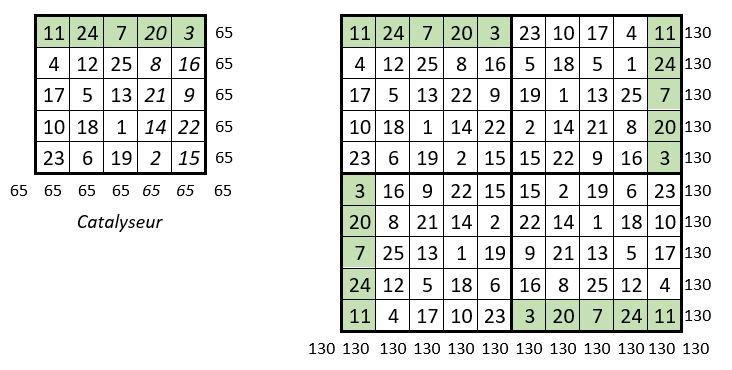
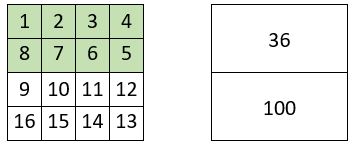
Dans le premier quartier de la grille d’ordre n = 10 de 100 cases, on place un carré magique normal d’ordre n = 5, de Constante magique M5 = 65, considéré comme catalyseur.
On place ensuite ce même carré magique, dans le second quartier, après lui avoir fait subir une rotation d’un quart de tour vers la droite.
On place alors ce dernier carré magique dans le troisième quartier, après lui avoir fait subir également une rotation d’un quart de tour vers la droite.
On procède enfin de la même façon pour ce dernier carré magique, que l’on place dans le quatrième quartier de la grille d’ordre n = 10.
On obtient un carré magique répétitif de Cte mag. M’10 = 130.
C’est bien sûr un carré magique répétitif à quartiers égaux, de Somme : S = 325.
On peut choisir comme catalyseur n’importe quel carré magique normal, de tout ordre. Il y a ainsi de nombreuses applications de cette méthode.
Construction d’un carré magique répétitif d’ordre n = 12
Une proposition de Hannes Bürgel
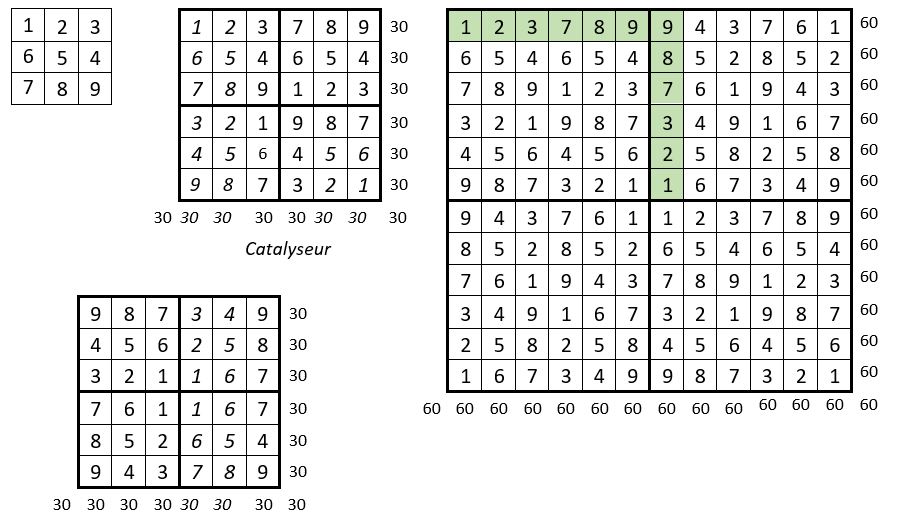
On construit tout d’abord le carré Catalyseur d’ordre n = 6, avec pour base le carré naturel alterné d’ordre n = 3. Ce catalyseur est en fait un carré magique répétitif, d’ordre n = 6 et de Constante magique M6 = 30, construit en application de l’une ou l’autre des méthodes exposées ci-dessus.
On place ce Catalyseur, tel quel, dans les quartiers 1 et 3 de la grille d’ordre n = 12 de 144 cases, préparée à cet effet.
On place encore ce Catalyseur dans le quartier 2, après une rotation d’un quart de tour vers la gauche.
Enfin on place cette dernière forme du Catalyseur, dans le quartier 4 de la grille d’ordre n = 12.
On obtient un carré magique répétitif, pas très diversifié, d’ordre n = 12, de Constante magique M12 = 60.
Le carré central d’ordre n = 6, reproduit ci-dessus, à gauche, est également un carré magique répétitif de Constante magique M6 = 30
retour à l’Introduction partie précedente partie suivante