Introduction Partie 1 Partie 2 Partie 3 Partie 4
Sommaire
- 1 Construction d’un carré magique répétitif d’ordre n=16
- 1.1 Un beau carré magique répétitif d’ordre n = 16
- 1.2 Exemple de carré semi-magique répétitif d’ordre n = 16
- 1.3 Autre structure de carré semi-magique répétitif d’ordre n = 16
- 1.4 Une construction du carré magique répétitif d’ordre n = 16
- 1.5 Le pavé d’assemblage dans tous ses états.
- 1.6 Une variante des quatre carrés formateurs
- 2 Le carré naturel formateur
Construction d’un carré magique répétitif d’ordre n=16
Un beau carré magique répétitif d’ordre n = 16
Une proposition de Hannes Bürgel
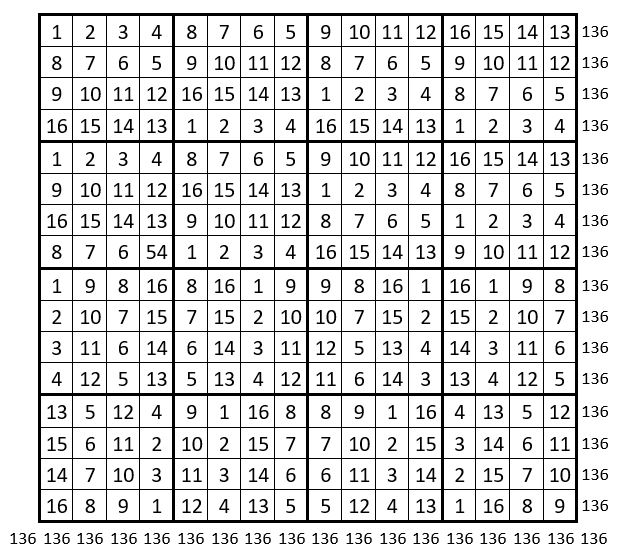
Dans la demie-grille supérieure du carré magique potentiel, les 8 sous-carrés de 16 cases sont issus de 8 permutations des lignes du carré naturel alterné normal d’ordre n = 4, lequel figure dans le premier sous-carré de la première rangée de sous-carrés.
Notons que ces 8 permutations sont prises parmi les N = 4 ! = 24 permutations possibles de ces 4 lignes.
Dans la demie-grille inférieure, on considère les 8 permutations des 4 colonnes de l’une des formes du carré naturel alterné normal d’ordre n = 4, forme ayant subie une rotation d’un quart de tour du carré naturel alterné normal d’ordre n = 4, laquelle forme figure enfin dans le premier sous-carré de la 3ème rangée de sous-carrés.
Ces 8 permutations font également partie des N = 24 permutations possibles des 4 colonnes.
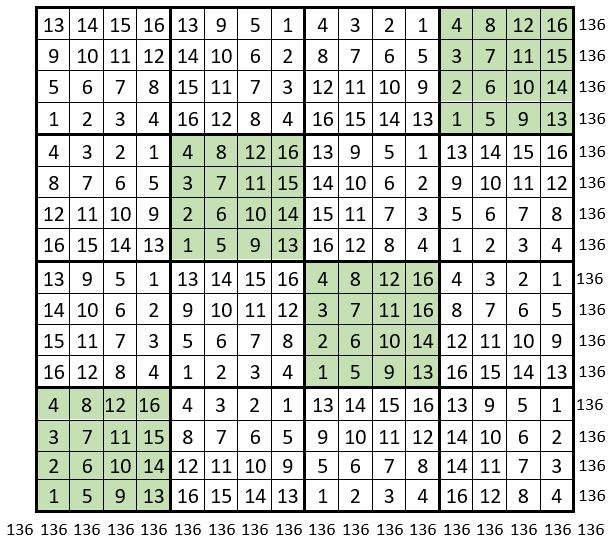
On obtient un carré magique répétitif d’ordre n = 16, de Constante magique : M16 = 136.
Les 16 termes des 16 sous-carrés de 16 cases, ont tous, par construction, la même somme : S= 136, somme qui apparait ainsi 50 fois dans ce carré magique répétitif.
L’application de ces quelques règles, ainsi décryptées, conduit peut-être à d’autres solutions ? Hannes Bürgel, l’auteur de ce carré magique répétitif original, le qualifie de « Perfekt, aber sehr kompliziert ! »
Exemple de carré semi-magique répétitif d’ordre n = 16

Autre structure de carré semi-magique répétitif d’ordre n = 16
Une proposition de Hannes Bürgel
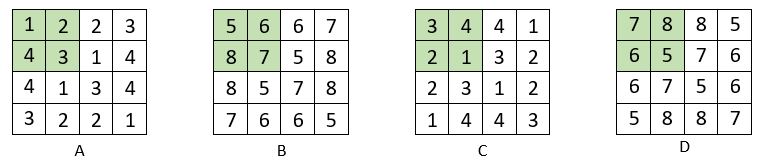
On construit tout d’abord quatre carrés numériques formateurs ou catalyseurs,
A, B, C, D, en utilisant de la même façon les deux suites de 4 termes des 8 premiers entiers : « 1, 2, 3, 4 » et « 5, 6, 7, 8 ». On place alors ces carrés formateurs dans la grille d’ordre n = 16, de 256 cases, conformément au tableau de placement ci-contre.
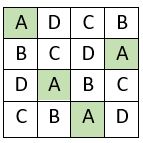
On obtient un carré semi-magique répétitif d’ordre n = 16, et de Constante magique M16 = 72. Les diagonales centrales ne sont pas magiques.
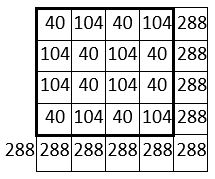
Les sommes des termes des 16 carrés formateurs catalyseurs, forment elles-mêmes un carré magique répétitif de Constante magique M’4 = 288 ( ci-contre )
Une construction du carré magique répétitif d’ordre n = 16
Une proposition de Hannes Bürgel
Cette construction, est remarquable, en ce sens qu’elle repose uniquement sur le carré naturel normal d’ordre n = 4. Celui-ci peut être considéré comme de pilier, le pivot de cette construction originale, l’unique source.
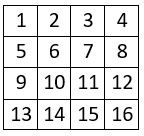
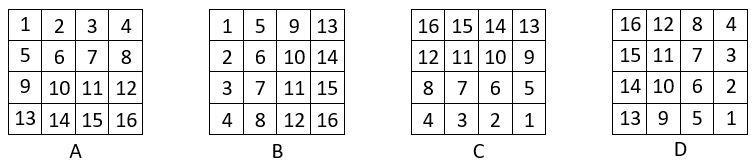
On construit les quatre carrés formateurs ou catalyseurs « A, B, C, D », ainsi qu’il suit :
▶ Carré « A » : c’est le carré naturel normal d’ordre n = 4, tel qu’il se présente.
▶ Carré « B » : on fait subir au carré « A » une rotation d’un quart de tour vers la gauche, et on adopte le symétrique par rapport au côté supérieur.
▶ Carré « C » : on fait subir une rotation d’un demi- tour au carré « A », et on le reproduit tel quel.
▶ Carré « D » : on fait subir une rotation vers la gauche de trois quarts de tour au carré « A », et l’on retient le symétrique par rapport au côté supérieur.
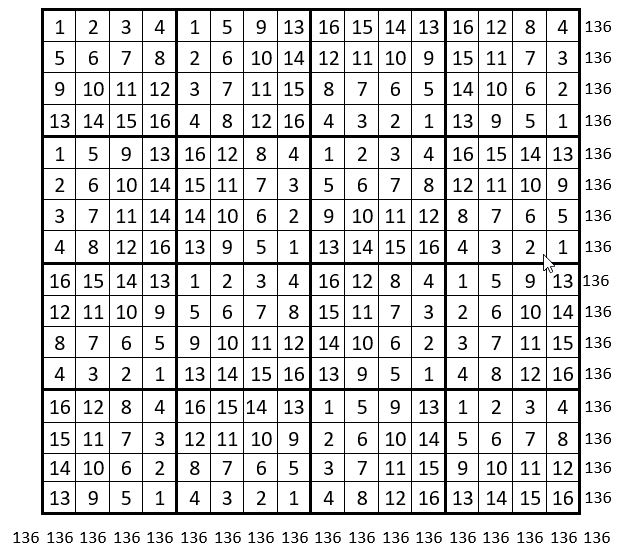
On place alors ces carrés formateurs dans la grille d’ordre n = 16 préparée à cet effet, conformément au pavé d’assemblage ci-contre : on remarque, dans ce pavé d’assemblage, que les carrés de même indice, sont situés sur une permutation figurée. On obtient un carré magique répétitif d’ordre n = 16, de Constante magique M16 = 136.
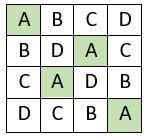
Quelques propriétés des carrés formateurs d’ordre n = 4 :
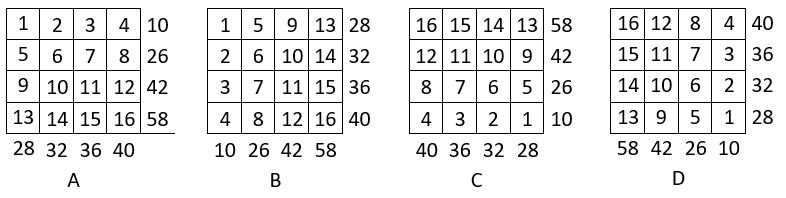
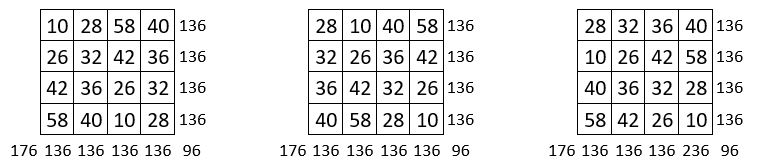
▶Les sommes des termes des lignes homologues des carrés formateurs, forment un carré semi-magique répétitif ( carré de gauche ci-dessus )
▶De même, les sommes des termes des colonnes homologues, forment un carré semi-magique répétitif ( carré central ci-dessus )
▶Ces deux grilles sont symétriques, après une rotation d’un quart de tour de l’une d’entre elles.
▶Enfin si l’on place dans la première ligne, les sommes des quatre premières colonnes, dans la seconde ligne, les sommes des quatre colonnes suivantes, et ainsi de suite, on obtient un carré semi-magique répétitif d’ordre n = 4 et de Constante magique M’4 = 136 ( carré de droite ci-dessus )
Le pavé d’assemblage dans tous ses états.
Rappelons la remarque ci-dessus : dans le pavé d’assemblage, les carrés formateurs de même indice sont situés sur une permutation figurée. Alors, mettant à profit cette remarque, construisons un pavé d’assemblage présentant ces propriétés, ci-contre.
On place alors dans une grille d’ordre n = 16, les mêmes carrés formateurs que précédemment, mais en observant l’assemblage du nouveau pavé d’assemblage ci-dessus.
La grille obtenue ( ci-dessous ) est un carré magique répétitif d’ordre n = 16, de Constante magique M’16 = 136.
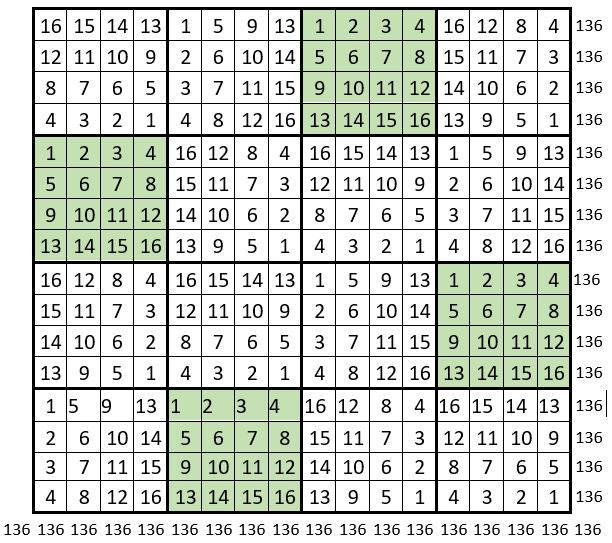
On peut ainsi augurer que tout pavé d’assemblage d’ordre n = 4, comportant les quatre carrés formateurs situés sur une permutation figurée, conduit à un carré magique répétitif d’ordre n = 16, et de Constante magique M’16 = 136.

On peut construire ( ci-dessus ) au moins six pavés d’assemblage présentant la propriété rappelée ci-dessus, conduisant ainsi à six solutions, quant au carré magique répétitif d’ordre n = 16.
Une variante des quatre carrés formateurs
Voici une variante des quatre carrés formateurs, avec toujours une forme du carré naturel d’ordre n = 4 pour origine.
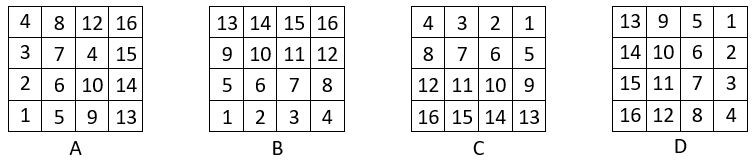
On adopte pour pavé d’assemblage, le pavé ci-contre :
On obtient le carré magique répétitif ci-contre, d’ordre n = 16, et de Constante magique M16 = 136.
Le carré naturel formateur
Le carré naturel reste un formateur privilégié pour la construction des carrés magiques répétitifs.
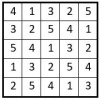
Voici tout d’abord les 8 formes du carré naturel normal d’ordre n = 3, pris pour exemple dans notre exposé.
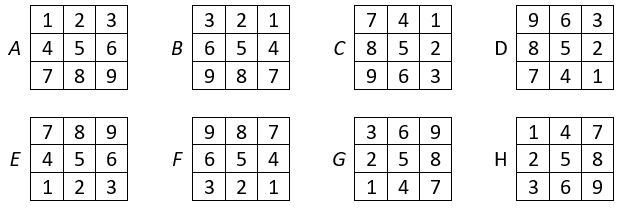
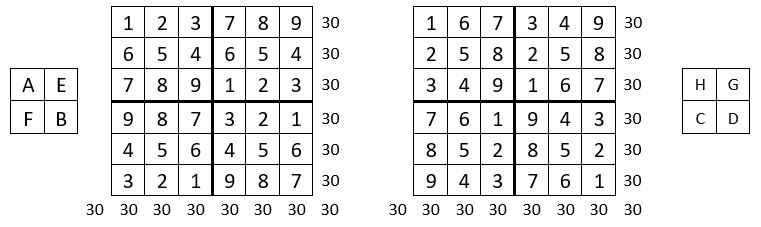
On place dans la grille d’ordre n = 6 de 36 cases, les formes du carré naturel, conformément aux petits pavés d’assemblage correspondants, situés de part et d’autre des grilles d’ordre n = 6.
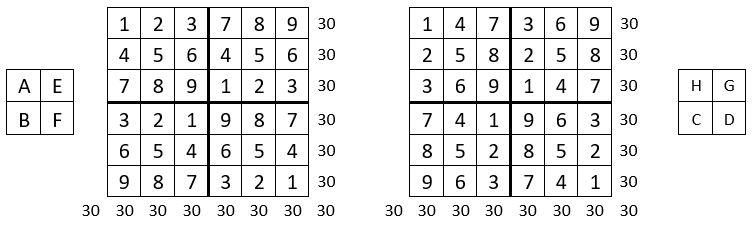
On obtient un carré magique répétitif d‘ordre n = 6, et de Constante magique M6 = 30.
Il y a d’assez nombreuses solutions, tributaires des pavés d’assemblage.
Les pavés d’assemblage correspondent aux combinaisons de 8 termes pris 4 à 4, soit = 70. Et, dans chaque pavé, les indices peuvent être placés de : N = 4 ! = 24 façons différentes.
On aurait ainsi, dans le cas qui nous occupe, à tester : N = 70 x 24 = 1 680 grilles !
On procède à la même analyse systématique avec le carré naturel alterné d’ordre n = 3.
Voici les huit formes du carré naturel alterné d’ordre n = 3 :
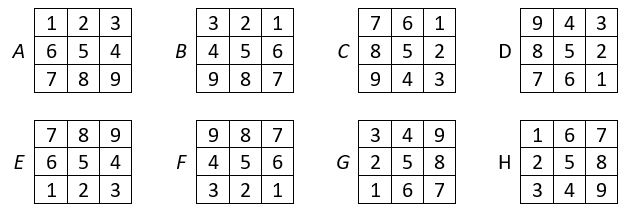
Et deux solutions de l’application correspondante ; le dénombrement est identique ( voir ci-dessus )