Introduction Partie 1 Partie 2 Partie 3 Partie 4
Sommaire
Construction d’un carré magique répétitif d’ordre n=6
Une méthode de construction prolifique
Retrouvons une construction simple du carré magique ou semi-magique répétitif. Soit par exemple dans la grille d’ordre n = 6 de 36 cases.
On choisit une permutation figurée ; précisons déjà que l’on a le choix entre :
6 ! = 720 permutations figurées possibles dans la grille d ’ordre n = 6.
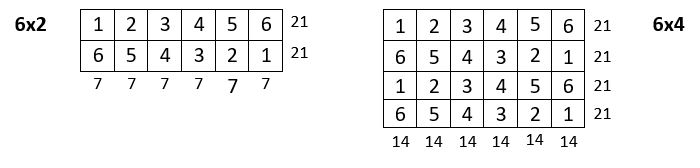
On place l’un des termes des six premiers entiers, sur chaque terme de la permutation figurée choisie, soit par exemple l’unité ( ci-contre )
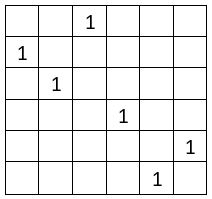
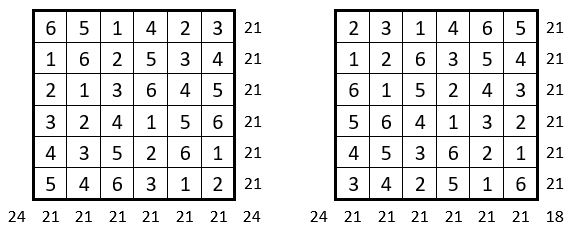
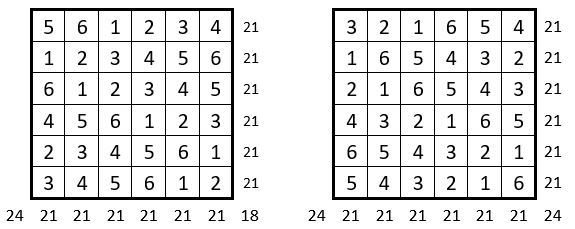
On complète alors la série des 6 premiers entiers dans les colonnes, en descendant ou en remontant, ainsi que dans les lignes, de droite à gauche ou de gauche à droite : voici ci-dessus ces quatre possibilités.
On obtient un carré semi-magique répétitif d’ordre n = 6, et de Constante magique M’6 = 21, et c’est un carré semi-magique répétitif à quartiers opposés égaux.
Le choix du terme placé sur la permutation figurée conduit à 6 solutions ; on a le choix parmi les 720 permutations figurées d’ordre n = 6 ; et enfin il y a 4 solutions issues du remplissage de la grille. Ainsi au total, dans la grille d’ordre n = 6, on aura : N6 = 6 x 720 x 4 = 17 280 solutions.
Cette construction, applicable à tout ordre de la grille du carré semi-magique répétitif, peut donc être considérée comme particulièrement prolifique.
Un carré semi-magique répétitif d’ordre n = 6
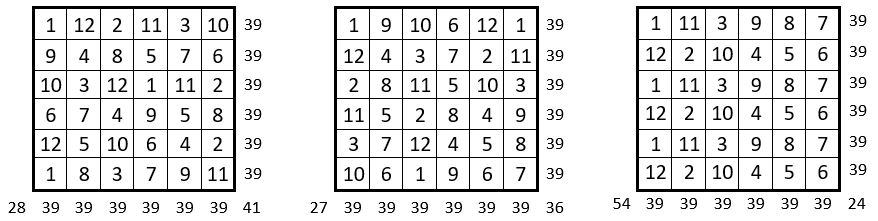
Voici une petite série de carrés semi-magiques répétitifs d’ordre n = 6, de Constante magique M’6 = 39 : la suite des 12 premiers entiers y figure trois fois.
Chacun des 9 sous-carrés de 4 cases a pour somme S = 26. Et ce sont des carrés semi-magiques répétitifs à quartiers opposés égaux.
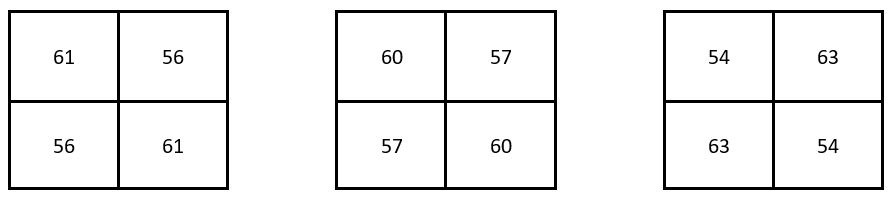
Dans le cas particulier qui nous occupe, certains auteurs nomment cette catégorie de carrés semi-magiques répétitifs, des carrés magiques de triplets.
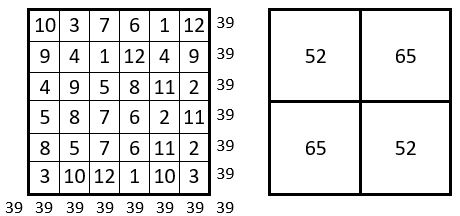
Voici quand même un vrai carré magique répétitif d’ordre n=6, de Constante magique M’6 = 39 ; comme dans les cas qui précèdent, les 9 sous-carrés de 4 cases ont pour somme : S = 26, et c’est un carré magique répétitif à quartiers opposés égaux.
Une méthode de construction serait la bienvenue.
Une panoplie de la grille d’ordre n = 6
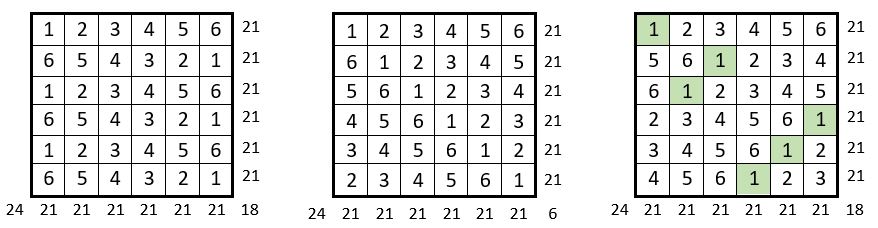
Je propose une récapitulation des sept options de carrés magiques répétitifs dans la grille d’ordre n = 6 de 36 cases, choisie comme exemple.
Lorsque l’on a sélectionné la magie dans les colonnes ( option « c » par exemple ) on obtient la magie dans les lignes par application de la Méthode des permutations dans les colonnes, ce qui n’altère pas la magie dans ces colonnes ( voir exemple « c » ci-dessous ).
Certaines options donnent directement un carré semi-magique répétitif ( a, b, d, g )
Les 18 premiers entiers répétés 2 fois.
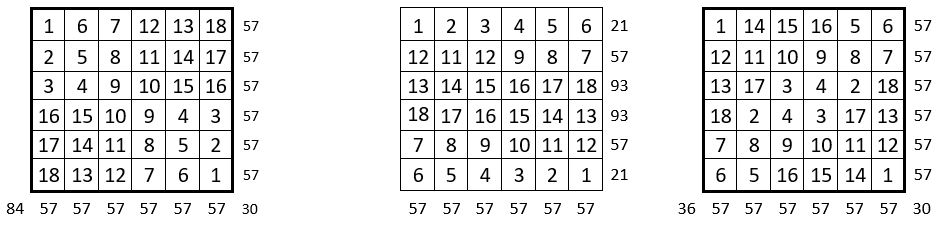
Les 2 premiers entiers sont répétés 18 fois
Le schéma des 18 placements répétés des deux premiers entiers dans cette grille, se décline au moins de trois façons différentes
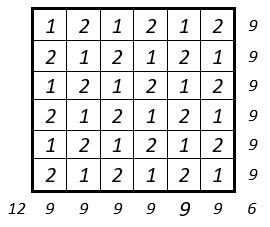
Les 12 premiers entiers sont répétés 3 fois.
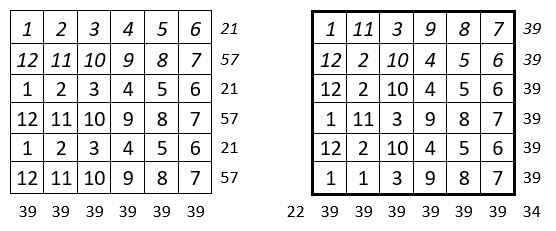
Les 3 premiers entiers sont répétés 12 fois.
Les 9 premiers entiers sont répétés 4 fois.
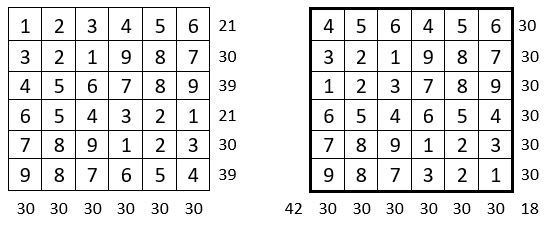
Les 4 premiers entiers sont répétés 9 fois.
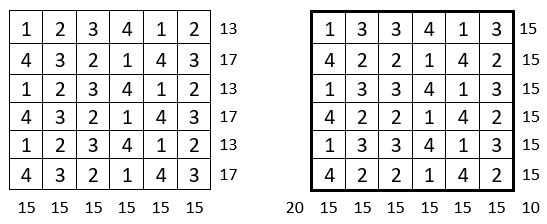
Les 6 premiers entiers sont répétés 6 fois.
Il y a de nombreuses solutions.
On peut ainsi dresser une panoplie des carrés magiques ou semi-magiques répétitifs de toute grille carrée d’ordre n. Cependant les grilles dont l’ordre « n » est un nombre premier ( ainsi n = 7 par exemple ) n’ont qu’une seule option, soit la répétition n fois des n premiers entiers ( option g )
Le carré magique répétitif d’ordre n = 3
Le carré magique répétitif non normal
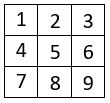
On se propose de regrouper par 3 les 9 premiers entiers de la grille d’ordre n = 3,∁ ce qui correspond à la combinaison de 3 termes pris 3 par 3, soit ![]()
Prenons, pour notre analyse, l’une de ces 84 combinaisons, soit par exemple la série : 4, 8, 6.
Et utilisons la Méthode des permutations figurées pour la construction du carré magique répétitif.
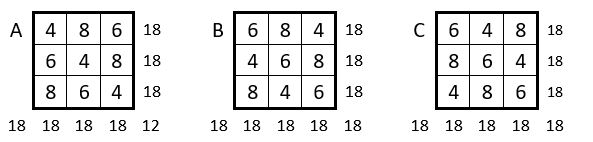
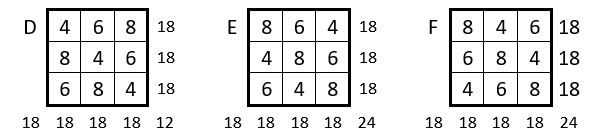
La série « 4, 8, 6 » se présente sous 6 permutations différentes : A, B, C, D, E, F.
Les 6 grilles ci-dessus sont construites par la même application diagonale de la Méthode des permutations figurées, qui compte en fait elle-même 6 applications différentes.
Ainsi chaque série compte 6 solutions.
Au total, on aurait donc au moins pour ce cas de n = 3 : N3 = 84 x 6 x 6 = 3 096 solutions.
Bien sûr, on peut procéder à une analyse analogue pour tout ordre de la grille prise pour exemple, et dénombrer les solutions correspondantes.
Le carré magique répétitif d’ordre n = 3. Une panoplie.
On se propose de poursuivre l’analyse du carré magique répétitif d’ordre n= 3 sur un thème différent.
Peut-on dénombrer et cataloguer les carrés magiques répétitifs d’ordre n = 3, magiques dans les lignes, les colonnes et les deux diagonales, ( ou « entiers » ) comme les grilles B et C ci-dessus, parmi les 84 séries ou combinaisons présentées ci-dessus ? Le travail a été fait ( Kirk T. McDonald – 3 x 3 Magic Squares with Duplicate Digits Allowed – Princeton University – N.J. 08544 – October 13. 2001. ).
Je m’en suis inspiré dans les pages qui suivent.
Notons quand même que les grilles B et C appartiennent à la même solution, aux symétries près.
Tout d’abord, on remarque que les carrés magiques répétitifs d’ordre n = 3, constitués d’un chiffre, répété 9 fois, conviennent tout-à-fait. Ces carrés magiques répétitifs nous donnent les 9 constantes magiques possibles dans cette catégorie de carrés magiques répétitifs d’ordre n = 3.
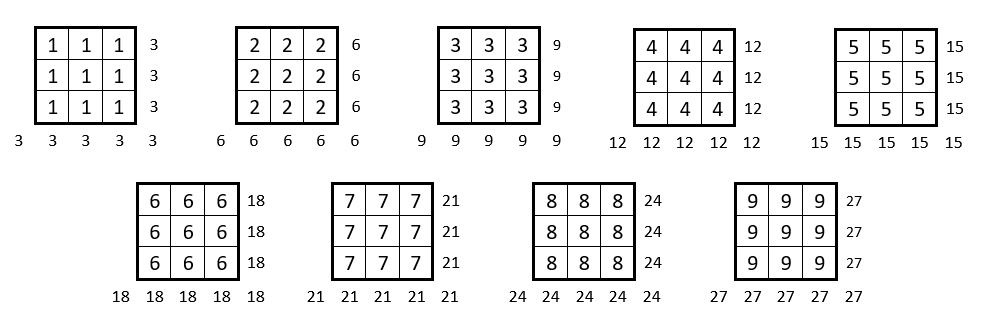
Il reste donc à tester : 84 – 9 = 75 séries de 3 termes. On laissera donc de côté, à titre provisoire, les 9 carrés magiques répétitifs formés d’un seul chiffre.
On classe alors ces carrés magiques répétitifs en fonction de la valeur de leur constante magique.
Constante magique M3 = 6 : Il n’y a qu’une solution.
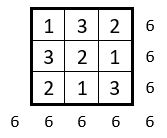
Constante magique M3 = 9 : Il y a 3 solutions.
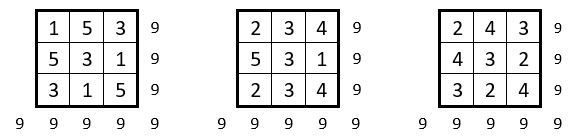
Constante magique M3 = 12 : On dénombre et catalogue 5 solutions

Constante magique M3 = 15 : Il y a 8 solutions
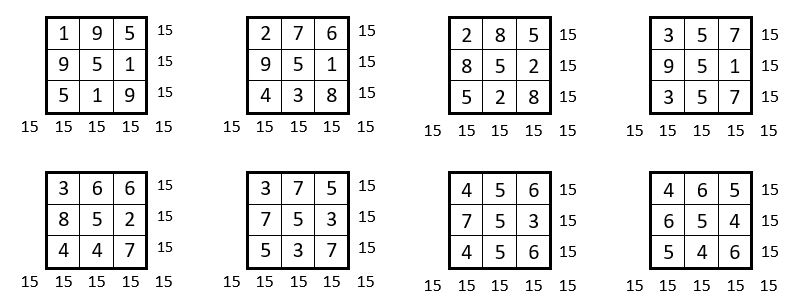
Constante magique M3 = 18 : Il y a 5 solutions

Constante magique M3 = 21 : Il y a 3 solutions
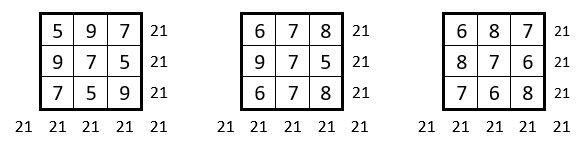
Constante magique M3 = 24 : Il y a 1 solution
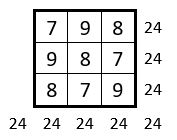
Constante magique M3 = 27 : Il n’y a pas de solution, en dehors du carré magique répétitif comptant le chiffre 9 répété 9 fois.
Ainsi, sur les 84 séries de 3 termes de la grille d’ordre n = 3, on dénombre et catalogue comme carré magique répétitif « entiers », 9 carrés magiques répétitifs constitués d’un seul chiffre, et 26 carrés magiques répétitifs « entiers ».
Un carré magique normal d’ordre impair
Le carré magique ou semi-magique répétitif participe à la construction des carrés magiques normaux d’ordre impair, dans une méthode de construction simple.
En voici deux exemples.
Application pour n=5
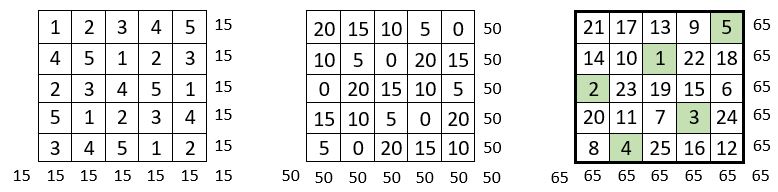
On construit, de façon classique, deux carrés magiques répétitifs auxiliaires, d’ordre n = 5 :
. Le premier avec les n = 5 premiers entiers répétés cinq fois ;
. Le second avec la série de « n » termes, « 0, n, 2n, 3n, 4n », soit « 0, 5, 10, 15, 20 », répétée aussi cinq fois.
On ajoute terme à terme ces deux grilles auxiliaires. On obtient un carré magique normal d’ordre n = 5, et de Constante magique M5 = 65.
Les termes des sous-séries de n = 5 termes de ce carré magique normal, sont situés sur une permutation figurée.
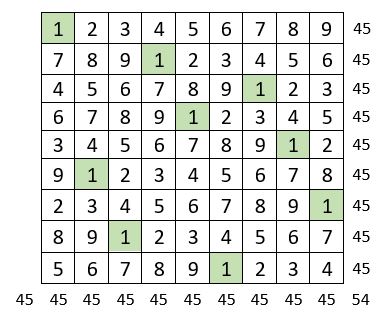
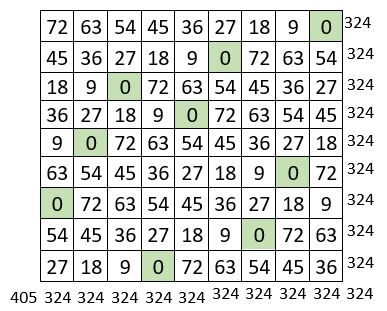
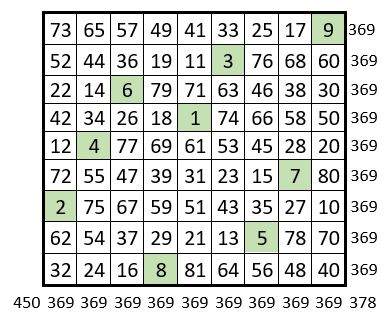
Application pour n=9
. Le premier carré auxiliaire, un carré semi-magique répétitif, utilise les 9 premiers entiers répétés 9 fois ;
. Le second carré auxiliaire, avec n = 9, utilise la série : « 0, n, 2n, 3n, 4n, 5n, 6n, 7n, 8n »,
soit « 0, 9, 18, 27, 36, 45, 54, 63, 72 », répétée également 9 fois ; c’est bien un carré semi-magique répétitif.
La Constante magique du carré magique normal obtenu par addition, terme à terme, des deux carrés auxiliaires, est la somme des constantes magiques de ces deux carrés auxiliaires : 45 + 324 = 369. Remarque analogue en ce qui concerne la somme des diagonales centrales.
Dans le carré magique normal d’ordre n = 9 final, les termes des 9 sous-séries de 9 termes, sont situés sur une permutation figurée.
Il y a de très nombreuses solutions. Au moins : N9 = 9 ! x 9 ! = 362 880 x 362 880 = un très grand nombre . . .
Cette méthode de construction des carré magiques normaux d’ordre impair, avec la participation des carrés magiques répétitifs auxiliaires, peut être considérée comme très prolifique.
Un carré magique répétitif d’ordre pair
Application pour n=4
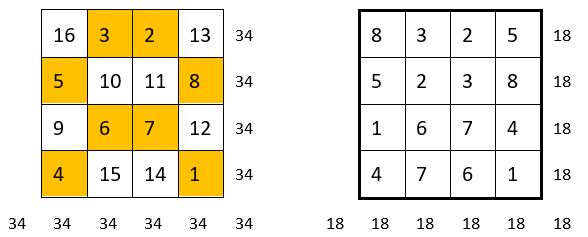
On choisit comme catalyseur un carré magique normal d’ordre n = 4 .
On considère la première moitié des nombres consécutifs formant le carré magique, soit la série « 1 – n2 », et dans ce cas « 1 – 16 », à leur place définitive dans la grille du carré magique à construire, soit les nombres depuis 1 jusqu’à 8 : termes pochés dans le catalyseur à gauche ci-dessus.
On diminue alors les autres nombres de n2/2 = 8 unités. On obtient un carré magique répétitif, de Constante magique M4 = 18. La série des nombres « 1 – 8 » est répétée deux fois.
Application pour n=6
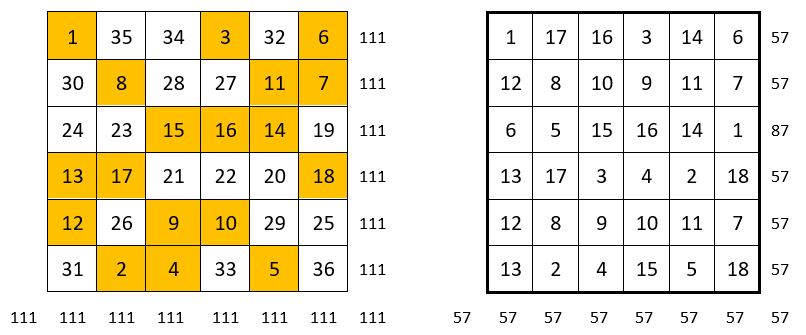
Dans ce cas particulier, on maintient en place les nombres de la série « 1 -18 » pris dans le carré magique catalyseur d’ordre n = 6. et l’on diminue les autres nombres de n2/2 = 18 unités.
On obtient un carré magique répétitif de Constante magique M6 = 57.
La série « 1 – 18 » est répétée deux fois.
C’est en partie un carré magique de type associé : les nombres situés sur les deux diagonales centrales possèdent seuls cette propriété ; la Constante de polarisation est P6 = 19.
Les rectangles magiques répétitifs
Il n’y a qu’une seule forme de rectangle magique répétitif correspondant à la relation 1n x 2k.
Cette relation englobe le carré magique répétitif lorsque n=2k.

Un carré magique répétitif issu du cube magique.
On assemble les 9 coupes orthogonales magiques ou semi-magiques d’un cube magique d’ordre n = 3.
Voici tout d’abord ces 9 coupes :
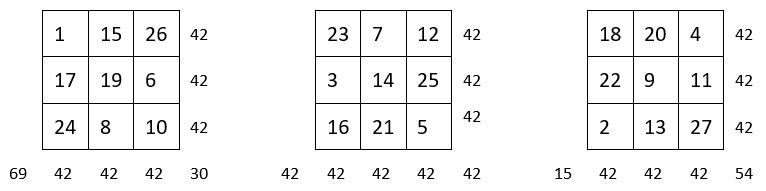
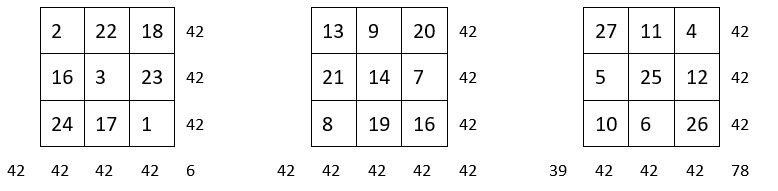
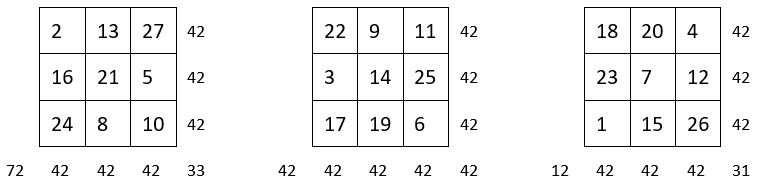
On assemble alors ces 9 coupes telles qu’elles se présentent :
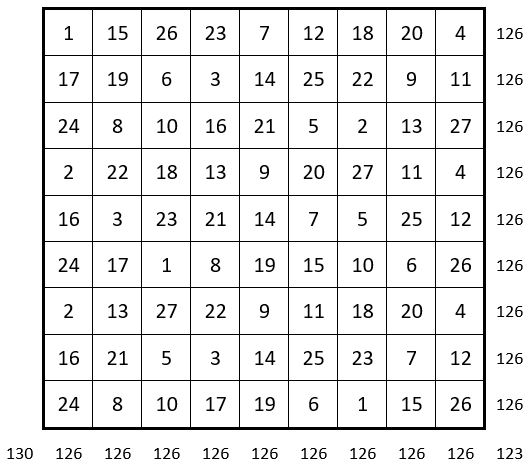
On obtient un carré magique répétitif, de Constante magique M9 = 126 = 42 x 3 .
La suite des 27 premiers entiers est répétée 3 fois.
L’ordre d’assemblage de ces couples est quelconque. On compte : N = 9 ! = 362 880 solutions.