El-Bouni, qui décrit cette méthode de construction des carrés magiques à enceinte(s) d’ordre impair, est originaire de Bône (Algérie) ; il est mort en 1225. On peut situer l’ouvrage dans lequel il traite des carrés magiques, au début du XIIIème siècle. D’après le traducteur/commentateur de El-Bouni, l’origine persane de cette méthode transparaît dans le texte arabe. El-Bouni, cabaliste très connu à son époque, ne semble pas être l’inventeur de ladite méthode, dont l’ancienneté ne fait cependant aucun doute.
Cette méthode est exposée par Carra de Vaux, « Une solution arabe du problème des carrés magiques » dans la Revue d’histoire des sciences,1947,pp 206-242.

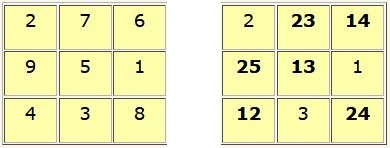
Soit l’exemple d’un carré d’ordre n = 5 . On procède de l’intérieur vers l’extérieur.
Remplissage du carré central d’ordre n = 3.
On part de l’une des formes du Lo Shu :
Soit » n’ » l’ordre de l’enceinte ;
dans notre exemple, on a n’ = 5
Aux termes de la diagonale composée des chiffres médians (4,5,6) de la suite naturelle des entiers de 1 à 9, on ajoute la demi différence des carrés de n’ et n :
D/2 = ½ (n’2 – n2)
Dans notre exemple, avec n’ = 5 et n = 3, on aura :
D/2 = ½(n’2 – n2) = ½ (52 –32 )= 8
On remarque que les nombres obtenus sont des nombres consécutifs.
Aux autres chiffres, supérieurs au médian (5), c’est-à-dire à 7, 8 et 9, on ajoute la différence des carrés mentionnés ci-dessus : D = n’2 – n2
Dans notre exemple, on aura : D = n’2 – n2 = 52 – 32 = 16
A noter que les trois premiers chiffres inférieurs au médian, restent à leur place définitive.
Remplissage de l’enceinte
On complète la seconde diagonale de manière à former une suite de nombres consécutifs : on place 11 et 15 dans les cases libres aux extrémités.
On place la suite 4, 5 et 6 dans les colonnes, en zig-zag horizontalement, au départ de la case située au-dessous du 15.
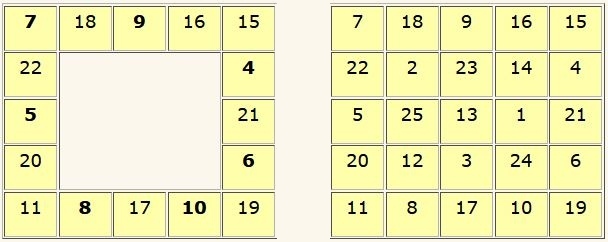
Puis on place la suite suivante, 7, 8, 9, 10 en zig-zag verticalement, au départ de la première case de la première ligne.
On complète enfin les cases opposées vis-à-vis par leurs complémentaires à n’2 +1 = 52+1 = 26.
La grille est alors complètement remplie. Constantes magiques M5 = 65 ; M’3 = 39.
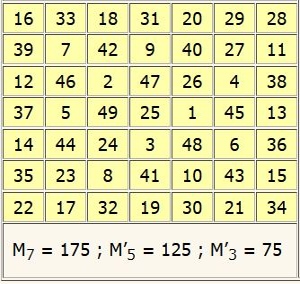
Voici deux autres exemples, construits avec la même méthode :