Sommaire
Introduction
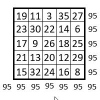
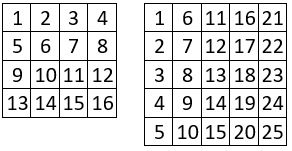
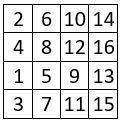
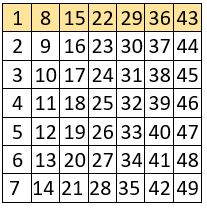
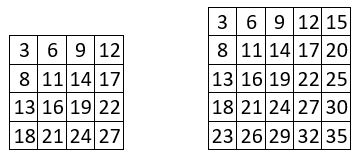
La méthode de construction du carré magique normal proposée, a pour origine la propriété suivante du carré naturel : Dans tout carré naturel, les termes des colonnes (ou des lignes) sont en progression arithmétique de raison r=n, tandis que les termes des lignes (ou des colonnes) sont dans l’ordre naturel, r=1.
On le vérifie aisément dans les carrés naturels d’ordre n = 4 et n = 5 ci-contre.
Méthode pour la construction d’un carré magique normal d’ordre n= 4
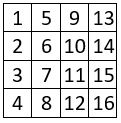
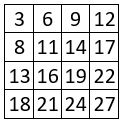
On sélectionne les quatre progressions arithmétiques qui se trouvent dans les lignes du carré naturel d’ordre n = 4, et on les aligne dans leur ordre naturel. On peut alors redistribuer les termes des progressions arithmétiques sélectionnées, à l’aide d’un catalyseur du même ordre que celui du carré magique potentiel.
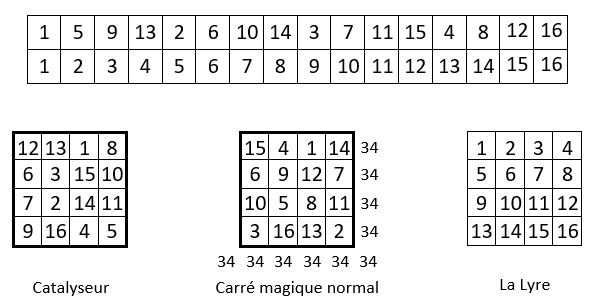
On obtient bien un carré magique normal d’ordre n = 4, de Constante magique M4 = 34.
Dans l’exemple donné, on a ainsi le choix pour le catalyseur, parmi les 880 carrés magiques de base d’ordre n = 4 de la Classification de Frénicle.
L’expérience montre que les progressions arithmétiques sélectionnées peuvent être alignées dans un ordre quelconque, sans perturber le développement de la méthode. Voici par exemple, dans le même ordre n = 4, un alignement différent des progressions arithmétiques sélectionnées ci-dessus, avec le même catalyseur :
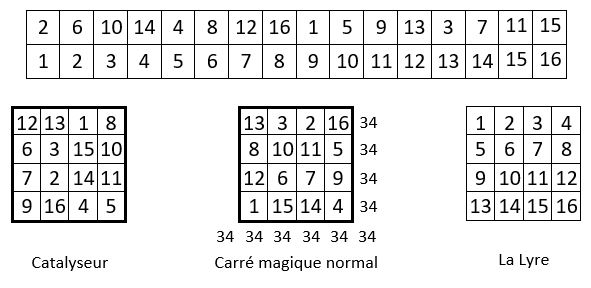
On obtient bien un carré magique normal d’ordre n = 4, et de Constante magique M4= 34.
Dans ce cas particulier de n = 4, il y a : 4 ! = 24 permutations possibles dans l’alignement des progressions arithmétiques sélectionnées.
On aura ainsi la possibilité de construire : N = 880 x 24 = 21 120 carrés magiques normaux d’ordre n = 4.
Application de la Méthode des progressions arithmétiques, pour l’ordre n = 7
J’ai choisi comme catalyseur le carré magique d’ordre n = 7 « Vénus », d’Agrippa de Nettesheim ( 1533 ).
Les progressions arithmétiques sélectionnées sont alignées dans leur ordre naturel. Le carré magique normal obtenu est de type associé, S7 = 50, Constante magique M7 = 175.
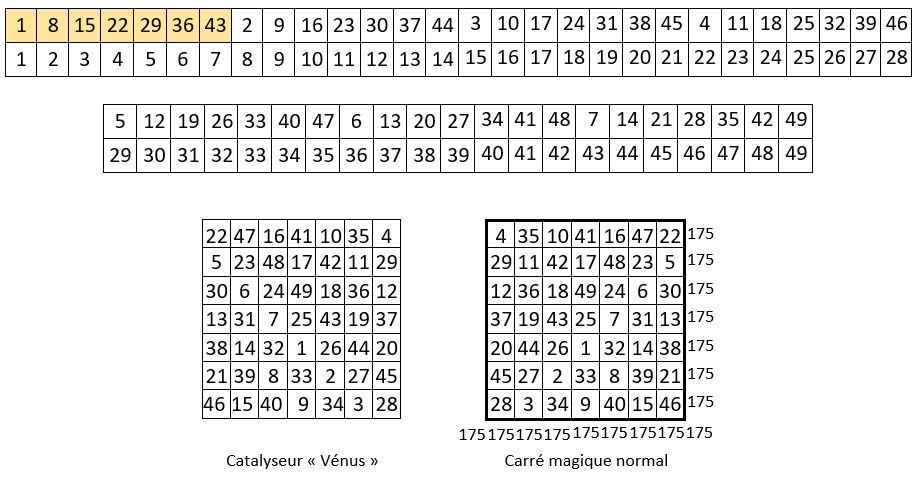
En ce qui concerne le catalyseur, on ne connait pas le nombre de carrés magiques normaux d’ordre n = 7, mais c’est un très grand nombre ; quant aux permutations des progressions arithmétiques sélectionnées, il y a : 7 ! = 5 040 permutations possibles. L’application de la Méthode des progressions arithmétiques conduit ainsi à la construction de très nombreux carrés magiques normaux d’ordre n = 7.
Généralisation
Alors s’impose l’idée de sélectionner des progressions arithmétiques sur le modèle des progressions arithmétiques du carré naturel, en observant les règles suivantes :
● Les « n » progressions arithmétiques sélectionnées de « n » termes ont la même raison « r ».
● Les têtes des « n » progressions arithmétiques sélectionnées sont elles-mêmes en progression arithmétique.
● Tous les termes de ces progressions arithmétiques sélectionnées sont différents.
Peut-on alors redistribuer les termes de ces progressions arithmétiques ainsi sélectionnées, en carré magique, en appliquant la méthode exposée ci-dessus ?
On maintient l’alignement des progressions arithmétiques sélectionnées dans leur ordre naturel.
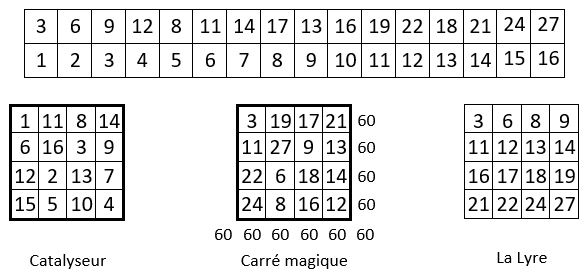
On obtient bien un carré magique, d’ordre n = 4, et de Constante magique M’4 = 60.
Certes, ce n’est pas un carré magique normal ( Voir la Lyre ). Ce carré magique présente cependant une propriété intéressante : Les huit diagonales des quatre quadrants ont même somme : S = 30, soit la moitié de la Constante magique ; une propriété héritée du catalyseur.
Considérons un second exemple, l’ordre naturel des progressions arithmétiques sélectionnées est maintenu. La méthode s’applique intégralement.
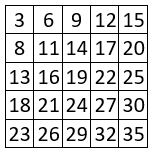
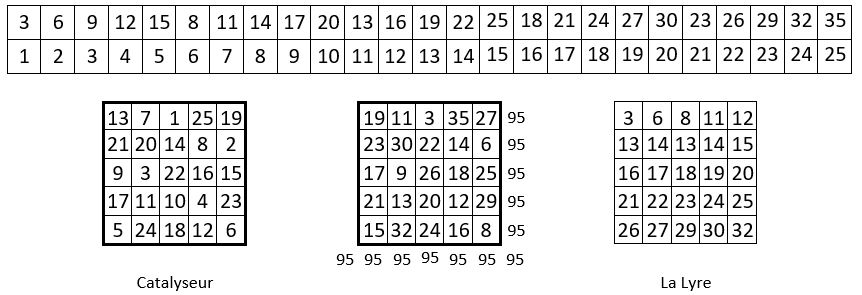
Le carré magique obtenu est pandiagonal : toutes les diagonales centrales et brisées sont magiques.
On compte 275 305 224 carrés magiques normaux d’ordre n = 5 comme catalyseur ; et l’on peut permuter les progressions arithmétiques sélectionnées de : 5 ! = 120 façons différentes.
En application de cette méthode, on peut ainsi construire un très grand nombre de carrés magiques d’ordre n = 5.
La Méthode originale des progressions arithmétiques, peut ainsi être considérée comme très prolifique.